
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Импульс тела. Второй закон Ньютона
Определение. Векторная величина р = m υ, где m ‑ масса частицы, υ ‑ её скорость, называется импульсом этой частицы. Второй закон Ньютона утверждает следующее: скорость изменения импульса частицы равна действующей на неё силе:
Далее мы будем иметь дело только с телами постоянной массы, и с учётом того, что р = m υ, а d υ /dt = a,уравнение (3.1) записывать в виде: m a = F. (3.2) Уравнение (3.2) читается так: произведение массы частицы на её ускорение равно силе, действующей на частицу. Если на частицу действует несколько сил, то под величиной F в (3.2) следует понимать их векторную сумму. Уравнение (3.2) часто удобнее записывать так: m Последнее векторное уравнение эквивалентно трём скалярным: m Уравнения (3.2) ‑ (3.4) называются уравнениями движения частицы. Замечание. В отличие от кинематических уравнений равномерного или равноускоренного движения, уравнения (3.2) ‑ (3.4) ‑ это динамические уравнения, или просто ‑ уравнения движения. Из уравнения (3.2) следует, что если на частицу не действует никакая сила, то её ускорение а = 0, т. е. скорость остаётся постоянной: υ = const. В системе СИ сила измеряется в ньютонах (Н): F = 1 Н ‑ это сила, которая телу массой m = 1 кг даёт ускорения а = 1 м/c2. Видно, что размерность силы [ F ] = [кг·м/с2]. Импульс силы Часто действие силы на частицу бывает настолько кратковременным, что мы имеем возможность наблюдать только начальный (р 1) и конечный (р 2) импульсы частицы. Тогда их связь с силой F можно получить лишь в некотором интегральном виде, проинтегрировав уравнение (3.1). Это даёт: р 2 − р 1 = где t 2 − t 1 = Δ t ‑ время действия силы. Определение. Величина
р 2 − р 1 = Δ р = < F >Δ t, (3.6) где < F > ‑ некоторое среднее значение силы на интервале времени Δ t. Таким образом, изменение импульса частицы равно произведению среднего значения силы на время её действия. Пример. Стальной шарик массой m = 100 г вертикально падает на стальную плиту со скоростью υ = 1 м/с и упруго отскакивает от неё с такой же скоростью. Время контакта шарика с плитой Δ t = 0,1 мс. Определить среднюю силу удара.
Движение частицы по окружности. Центростремительная сила При движении частицы по окружности радиусом R со скоростью υ частица испытывает центростремительное ускорение а ц.с = υ2/ R. Значит, по второму закону Ньютона, на частицу должна действовать какая-то сила, обеспечивающая это ускорение. Такая сила может быть любой природы: упругая (сила натяжения нити), кулоновская, гравитационная, сила трения. Или же комбинация (векторная сумма) этих сил. Определение. Сила любой природы, обеспечивающая движение частицы по окружности и обязательно направленная к центру этой окружности, называется центростремительной. Центростремительная - это обобщённое понятие силы, подобно тому как термин «еда» является обобщённым понятием хлеба, картошки, капусты. Поэтому нельзя говорить: «есть сила трения, сила упругости и т. д., а есть центростремительная». А следует говорить: «такая-то сила (трения, натяжения, гравитационная или их комбинация) в данной задаче является центростремительной F ц.с ». При описании динамики движения частицы по окружности надо исходить из уравнения движения по окружности: m a ц.с = m υ2 / R = F ц.с , (3.7) которое является конкретным применением второго закона (3.2) к движению по окружности. В этом уравнении F ц.с должна иметь конкретное содержание, оговоренное выше, т. е. в качестве F ц.с следует подставлять какую-то конкретную физическую силу в её проекции на радиус в направлении к центру, которая обеспечивает движение частицы по окружности. Пример 1. Шарик на нити длиной l, закреплённой на одном конце, движется в горизонтальной плоскости по окружности с угловой скоростью ω. Надо определить натяжение нити. Решение. Здесь роль центростремительно играет сила натяжения нити F н, поэтому уравнение движения шарика по окружности будет таким: F н = m ω2 l, где m ‑ масса шарика. Это и решает задачу. Пример 2. Спутник летает вокруг Земли по ближней круговой орбите, т. е. по орбите радиусом R ≈ R З = 6400 км. Найти период движения спутника.
Решение. Здесь центростремительной силой, обеспечивающей движение спутника по окружности, является гравитационная, которая на ближней орбите примерно равна mg, где m ‑ масса спутника, g = 9,8 м/с2. Следовательно, уравнение движения спутника по окружности будет таким: m ω2 R = mg. Отсюда период Т = 2π/ω = 2π Пример 3. Машина едет по закруглению дороги радиусом R = 80 м. При какой скорости машина не удержится на данном радиусе, если коэффициент трения колёс о дорогу k = 0,5. Решение. В этом примере центростремительной является сила трения F тр , так что уравнение движения машины по окружности будет таким: m υ2 / R = F тр . Пока машина удерживается на данном радиусе, сила трения здесь ‑ это сила трения покоя (сцепления с дорогой). По мере роста скорости растёт и сила трения покоя, удерживающая машину на дороге, но как только она достигнет своего максимального значения ‑ силы трения скольжения kmg, она уже не сможет удерживать машину на данном радиусе. Таким образом, максимальная скорость машины определяется уравнением: m υ2 / R = kmg. Отсюда υmax =
Решение. На шарик действуют две силы: сила тяжести m g и сила натяжения нити F, направленные под углом друг к другу (рис: 3.7), так что в этом примере центростремительной силой является их векторная сумма: F ц.с = m g + F н ,
m ω2 R = F ц.с , или: m ω2 l sin α = mg tg α. Отсюда, полагая, что α ≠ 0, угловая скорость ω = Пример 5. Машина едет со скоростью υ = 20 м/с (72 км/ч) по вогнутому участку дороги радиусом R = 20 м. Найти перегрузку водителя на нижнем участке такой дороги.. Решение. Перегрузка ‑ это отношение веса тела Р (тела шофёра) к силе тяжести mg, где m ‑ масса шофёра. Вес ‑ это сила давления тела на неподвижную относительно него подставку, в данном случае ‑ на кресло машины. А так как, по третьему закону Ньютона, с такой же силой и кресло давит на шофёра, то вес ‑ это фактически сила давления на тело неподвижной относительно него подставки (кресла): P = F давл. . Поэтому перегрузка μ = F давл. /mg. Значит, остаётся найти эту силу давления. Найдём её.
m υ2 /R = F давл.− mg. Деля это уравнение на mg, получаем, что шофёр испытывает трёхкратную перегрузку: μ =
|
||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.145.114 (0.013 с.) |
 . (3.1)
. (3.1) = F. (3.3)
= F. (3.3)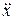 = Fx, m
= Fx, m  = Fy, m
= Fy, m  = Fz. (3.4)
= Fz. (3.4)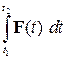 , (3.5)
, (3.5)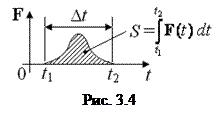 Уравнение (3.5) можно представить в виде:
Уравнение (3.5) можно представить в виде: Решение. Так как после удара импульс шарика меняется на противоположный, то Δ р = р 2 − р 1 = 2 р 2 = 2 m υ = 0,2 кг·м/с (рис. 3.5). Тогда, в соответствии с (3.6), средняя сила взаимодействия < F >= Δ р/ Δ t = 2000 Н. Во внесистемных единицах это около 200 кг силы.
Решение. Так как после удара импульс шарика меняется на противоположный, то Δ р = р 2 − р 1 = 2 р 2 = 2 m υ = 0,2 кг·м/с (рис. 3.5). Тогда, в соответствии с (3.6), средняя сила взаимодействия < F >= Δ р/ Δ t = 2000 Н. Во внесистемных единицах это около 200 кг силы.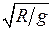 ≈ 84 мин.
≈ 84 мин. = 20 м/c = 72 км/ч.
= 20 м/c = 72 км/ч.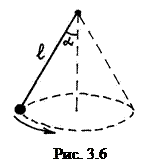 Пример 4 (к онический маятник). Шарик качается на нити длиной l, так что он движется по окружности, а нить ‑ по образующей конуса с углом α (рис. 3.6). Найти период движения шарика.
Пример 4 (к онический маятник). Шарик качается на нити длиной l, так что он движется по окружности, а нить ‑ по образующей конуса с углом α (рис. 3.6). Найти период движения шарика. которая обязательно должна быть направлена к центру окружности и обеспечивает движение шарика по этой окружности радиусом R = l sin α. Таким образом, уравнение движения шарика по окружности будет таким:
которая обязательно должна быть направлена к центру окружности и обеспечивает движение шарика по этой окружности радиусом R = l sin α. Таким образом, уравнение движения шарика по окружности будет таким: , а период Т = 2π / ω.
, а период Т = 2π / ω. При движении машины в нижней точке окружности на человека действуют две силы m g и F давл. (рис. 3.8), сумма которых в проекции на радиус по направлению к центру окружности О и является центростремительной силой. Так что в данном случае уравнение движения человека по окружности будет таким:
При движении машины в нижней точке окружности на человека действуют две силы m g и F давл. (рис. 3.8), сумма которых в проекции на радиус по направлению к центру окружности О и является центростремительной силой. Так что в данном случае уравнение движения человека по окружности будет таким: = 3.
= 3.


