
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение свободных синусоидальных колебаний
Определение. Дифференциальное уравнение второго порядка вида
Уравнение (9.1) называется так потому, что его общим решением является функция x (t) = X sin(ω t + φ), (9.2) описывающая синусоидальный колебательный процесс с угловой частотой ω и амплитудой Х. Период таких колебаний Т = 2π / ω (рис. 9.1). Амплитуда Х – это максимальное отклонение от положения равновесия. Выражение (ω t + φ), стоящее под знаком синуса, называется фазой колебаний, а угловой параметр φ – начальной фазой. Угловая частота ω имеет размерность «рад/с». Прямой подстановкой легко проверить, что функция (9.2) действительно является общим решением уравнения (9.1), т. е. обращает его в тождество. Значения параметров Х и φ в решении (9.2) определяются из начальных условий, т. е. из конкретного способа возбуждения колебаний. Эти конкретные способы будут рассмотрены в разделах 9.2 и 9.3. Однако в дальнейшем общее решение уравнения (9.1) удобно представлять не в виде (9.2) а таком: x (t) = А sin ω t +В cos ω t. (9.3) Коэффициенты А и В здесь легко пересчитываются через Х и φ по известной формуле синуса суммы. Если окажется, что движение какого-либо тела описывается дифференциальным уравнением вида (9.1), то это движение будет представлять собой синусоидальные колебания. Простейшими идеализированными механическими колебательными системами, в которых могут происходить незатухающие колебания, являются маятники: пружинный, математический и физический. Рассмотрим эти три вида маятников по отдельности.
Пружинный маятник Пусть груз массой m, лежащий на идеально гладкой горизонтальной плоскости, прикреплён к пружине жёсткостью k, которая другим концом закреплена на стенке (рис. 9.2, а). Очевидно, что если шарик вывести из положения равновесия и отпустить, то он будет совершать колебания. Поэтому такая колебательная система называется пружинным маятником. Покажем, что колебания груза в этом случае будут описываться уравнением (9.1).
Проведём ось х как показано на рис 9.2, а, приняв х = 0 в точке равновесия груза. Выведем груз из равновесия, сдвинув его на небольшое расстояние х вправо, и затем отпустим. По закону Гука, на груз при этом будет действовать упругая сила Fx = − kx, направленная против смещения (рис. 9.2, б). Тогда, в силу 2-го закона Ньютона, уравнение движения груза будет таким:
или:
или
где символом ω2 обозначено отношение k/m, т. е. ω = Видно, что уравнение движения груза (9.4) полностью совпадает с (9.1), следовательно, груз совершает синусоидальные колебания с угловой частотой (9.5). В общем виде эти колебания описываются функцией (9.3), в которой коэффициенты А и В определяются из начальных условий, т. е. из способа возбуждения колебаний груза. Начальными условиями для уравнения (9.4) являются значения координаты и скорости груза в начальный момент времени: х (0) и Вариант 1: груз оттянули вправо на заданное расстояние Х и отпустили. Тогда начальные условия запишутся так: х (0) = Х, υ(0) = Подставляя (9.3) в первое начальное условие, получаем: А sin 0 + B cos 0 = Х, откуда В = Х (коэффициент А пока не определён). Подставляя (9.3) во второе начальное условие, получаем:
х = Х cos ω t. (9.6) Вариант 2: груз толкнули из положения равновесия, т. е. в момент t = 0 при х = 0 ему сообщили начальную скорость υ0. В этом случае начальные условия будут иметь вид: х (0) = 0, υ(0) = Подставляя (9.3) в первое начальное условие, получаем: 0 = А sin 0 + B cos 0, откуда В = 0, т. е. теперь можно записать: х = А sin ω t. Подставляя это выражение во второе начальное условие, получаем: υ0 = А ω cos 0, т. е. А = υ0 / ω. И тогда при данном способе возбуждения закон колебаний груза будет иметь вид (рис. 9.1): х = Х sin ω t, (9.7) где В обоих вариантах частота колебаний одна и та же (формула 9.5), и она определяется только массой груза и жёсткостью пружины. Период колебаний
ПРИЛОЖЕНИЕ: закон Гука и энергия сжатой (растянутой) пружины. Закон Гука утверждает, что для сжатия или растяжения пружины на величину х, к ней надо приложить силу F, пропорциональную х: F = kx. Коэффициент пропорциональности k называется жёсткостью пружины. Если к пружине прикреплено какое-то тело (груз), то на него со стороны деформированной пружины будет действовать сила, пропорциональная деформации х и противоположно направленная этой деформации: Fх = − kx (рис. 9.2,б). Растягивая или сжимая пружину, сила F совершает работу А = в результате которой пружина приобретает потенциальную энергию W = Математический маятник Математическим маятником называется идеализированная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити. Хорошим приближением к математическому маятнику является небольшой тяжёлый шарик, подвешенный на длинной тонкой нити.
Замечание. В выражении αmax<< 1 угол α, конечно же, надо брать в радианах, т. е. α << 1 рад, т. е. α << 57º, т. е. α ≤ 5º. Таким образом, малым следует считать отклонение, не превышающее 5-6º. Из рис. 9.4 видно, что при малых отклонениях шарика возвращающая сила F = mg sin α ≈ mg (x/l). А так как эта сила направлена против смещения х, то в проекции на ось х следует записать: Fх = −mg (x/l). Тогда, по второму закону Ньютона, max = − или:
Видно, что это уравнение совпадает с (9.1), если обозначить
не зависит от массы шарика, а только от длины нити и ускорения свободного падания g в данном месте Земли. Коэффициенты А и В в общем решении (9.3) определяются из начальных условий, т. е. из способа возбуждения колебаний шарика: либо шарик отклонили на величину Х и отпустили (тогда х (0) = Х, υ(0) = х = Х cos ω t с периодом (9.8). Физический маятник Рассмотрим ещё одну колебательную систему – твёрдое тело произвольной формы, свободно качающееся на горизонтальной оси в поле тяжести. Такая система называется физическим маятником. Им может быть стержень на оси, кольцо или диск на оси, не проходящей через центр масс.
Поскольку здесь мы имеем движение твёрдого тела с закреплённой осью, то это будет вращательное движение и его следует описывать уравнением вращения:
I где I – момент инерции тела относительно оси вращения О, М – момент силы относительно этой же оси О, М = − mgl α. И тогда уравнение вращения тела примет вид:
где обозначено: ω2 = mgl / I. Видно, что это уравнение совпадает с (9.1), т. е. тело будет совершать синусоидальные колебания, описываемые функцией (9.3), и период этих колебаний
Если колебания физического маятника возбуждать, отклоняя тело на некоторый угол α0 и затем отпуская его, то, как и ранее, несложно показать, что они будут проходить по закону: α = α0 cos ω t с периодом (9.9).
Решение. Момент инерции кольца относительно точки подвеса О определяем из теоремы Штейнера: IО = IC + mR 2 = 2 mR 2. Следовательно,
Пример 2. Найти период колебаний стержня длиной а = 20 см, шарнирно закреплённого на верхнем конце. Решение. Момент инерции стержня относительно точки подвеса I = mа 2/3. Расстояние между точкой подвеса и центром масс l = а/ 2. Следовательно,
|
|||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.61.16 (0.021 с.) |
 , (9.1)
, (9.1)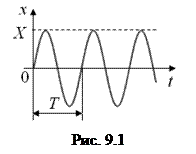 где символом
где символом 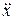 обозначена вторая производная по времени:
обозначена вторая производная по времени:  , называется уравнением свободных незатухающих синусоидальных (гармонических) колебаний. В этом уравнении х = х (t) – текущее смещение колеблющейся точки от положения равновесия, ω – параметр, называемый собственной частотой колебательной системы.
, называется уравнением свободных незатухающих синусоидальных (гармонических) колебаний. В этом уравнении х = х (t) – текущее смещение колеблющейся точки от положения равновесия, ω – параметр, называемый собственной частотой колебательной системы. max = − kx,
max = − kx, ,
, , (9.4)
, (9.4)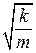 . (9.5)
. (9.5) (0) = υ(0). Рассмотрим два типичных способа возбуждения колебаний груза: 1) груз оттянули и отпустили; 2) груз толкнули из положения равновесия.
(0) = υ(0). Рассмотрим два типичных способа возбуждения колебаний груза: 1) груз оттянули и отпустили; 2) груз толкнули из положения равновесия. откуда А = 0. Таким образом, при данном способе возбуждения закон колебаний груза будет иметь вид (рис. 9.3):
откуда А = 0. Таким образом, при данном способе возбуждения закон колебаний груза будет иметь вид (рис. 9.3): − амплитуда колебаний.
− амплитуда колебаний. .
. ,
,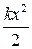 .
.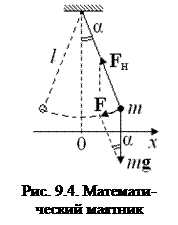 Итак, пусть шарик массой m подвешен на нити длиной l. Выведем его из равновесия и отпустим. Он начнёт качаться. Составим уравнение его движения и покажем. что оно совпадает с уравнением колебаний (9.1). Но это будет так лишь при условии, что колебания маятника будут малыми. Термин «малые» означает, что максимальное смещение Х шарика от положения равновесия (амплитуда колебаний) будет много меньше длины нити: Х << l (рис. 9.4). А это значит, что максимальный угол отклонения нити αmax<< 1, так как при небольших отклонениях sin α ≈ tg α ≈ α ≈ x/l.
Итак, пусть шарик массой m подвешен на нити длиной l. Выведем его из равновесия и отпустим. Он начнёт качаться. Составим уравнение его движения и покажем. что оно совпадает с уравнением колебаний (9.1). Но это будет так лишь при условии, что колебания маятника будут малыми. Термин «малые» означает, что максимальное смещение Х шарика от положения равновесия (амплитуда колебаний) будет много меньше длины нити: Х << l (рис. 9.4). А это значит, что максимальный угол отклонения нити αmax<< 1, так как при небольших отклонениях sin α ≈ tg α ≈ α ≈ x/l. ,
,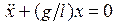 .
. , т. е. шарик будет совершать синусоидальные колебания, описываемые функцией (9.3), и период этих колебаний
, т. е. шарик будет совершать синусоидальные колебания, описываемые функцией (9.3), и период этих колебаний (9.8)
(9.8) Итак, пусть твёрдое тело подвешено на горизонтальной оси О (рис. 9.5). Как и для математического маятника, колебания будем считать малыми, т. е. угол отклонения α << 1 рад (57º), т. е. sin α ≈ α.
Итак, пусть твёрдое тело подвешено на горизонтальной оси О (рис. 9.5). Как и для математического маятника, колебания будем считать малыми, т. е. угол отклонения α << 1 рад (57º), т. е. sin α ≈ α. = I
= I  = M,
= M, − угловое ускорение тела. Из рис. 9.5 видно, что момент силы М = Fl = mgl sin α ≈ mgl α. Но так как этот момент является возвращающим, т. е. он действует на тело против направления отклонения α, то следует записать:
− угловое ускорение тела. Из рис. 9.5 видно, что момент силы М = Fl = mgl sin α ≈ mgl α. Но так как этот момент является возвращающим, т. е. он действует на тело против направления отклонения α, то следует записать: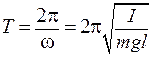 (9.9)
(9.9)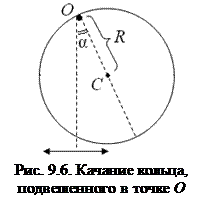 Пример 1. Найти период колебаний кольца радиусом R = 10 см, подвешенного на гвозде. Колебания происходят в плоскости кольца (рис. 9.6).
Пример 1. Найти период колебаний кольца радиусом R = 10 см, подвешенного на гвозде. Колебания происходят в плоскости кольца (рис. 9.6).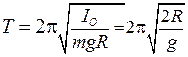 ≈ 0,9 с.
≈ 0,9 с. ≈ 0,73 с.
≈ 0,73 с.


