
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная энергия частицы в силовом поле
Важнейшим свойством потенциального силового поля F (х, у, z) является существование для него некоторой скалярной функции U (х, у, z), называемой потенциальной энергией частицы в этом поле. Выберем в потенциальном поле фиксированную точку М 0 и назовём её базовой. И пусть М (х, у, z) − другая, «переменная» точка в этом поле. В силу потенциальности поля F (х, у, z), его работа от точки М до базовой М 0 не зависит от формы траектории ММ 0 , а только от координат точки М (рис. 4.8):
Эта скалярная функция f называется потенциальной энергией частицы в силовом поле F (х, у, z) относительно выбранной базовой точки М 0 и обозначается символом U:
Формула (4.3) является определением потенциальной энергии частицы в точке М поля F (х, у, z). Таким образом, потенциальная энергия частицы в точке М относительно выбранной базовой точки М 0 − это работа поля F (х, у, z) по перемещению частицы из этой точки М в базовую по любому пути. Из формулы (4.3) видно, что потенциальная энергия частицы является величиной относительной, зависящей от выбора базовой точки М 0, поэтому при вычислении потенциальной энергии выбор базовой точки всегда оговаривается. Например, при вычислении потенциальной энергии частицы в однородном поле тяжести Земли базовая точка берётся на поверхности Земли. Если вычисляется потенциальная энергия частицы в поле одной или нескольких планет или звёзд, то принимается, что базовая точка М 0 находится в бесконечности. Замечание. При вычислении потенциальной энергии в место термина «работа поля» иногда удобнее пользоваться термином «работа внешней силы». Тогда потенциальная энергия частицы в точке М будет определяться как работа внешней силы F внеш. (мы работаем!) по перемещению частицы в точку М из базовой точки М 0:
Пример 1. Вычислить потенциальную энергию частицы массой m на высоте h над поверхностью Земли.
АОМ = Итак, искомая потенциальная энергия U = mgh. Пример 2. Вычислить потенциальную энергию планеты массой m на расстоянии r от Солнца. Масса Солнца
Таким образом, потенциальная энергия планеты в гравитационном поле звезды всегда отрицательна.
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.46 (0.005 с.) |

 .
. . (4.3)
. (4.3) .
. Решение. Так как здесь потенциальная энергия вычисляется относительно поверхности Земли, то и базовую точку М 0 следует брать на поверхности, а точку М − в любом месте на высоте h (рис. 4.9). Поскольку работа гравитационного поля F не зависит от формы пути, то выберем этот путь наиболее простым: ММ 0 = М О + ОМ 0 , как показано на рис. 4.9. Работа на участке ОМ 0 равна нулю, так как здесь мы движемся перпендикулярно силовым линиям поля F, а работа внешней силы на участке МО:
Решение. Так как здесь потенциальная энергия вычисляется относительно поверхности Земли, то и базовую точку М 0 следует брать на поверхности, а точку М − в любом месте на высоте h (рис. 4.9). Поскольку работа гравитационного поля F не зависит от формы пути, то выберем этот путь наиболее простым: ММ 0 = М О + ОМ 0 , как показано на рис. 4.9. Работа на участке ОМ 0 равна нулю, так как здесь мы движемся перпендикулярно силовым линиям поля F, а работа внешней силы на участке МО: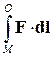 = mgh.
= mgh. .
. Решение. В астрономических системах потенциальную энергию тела принято вычислять относительно бесконечно удаленной точки М 0 . В этом случае, выполняя проход по радиусу от точки М (т. е. от радиуса r) до бесконечности (рис. 4.10) и учитывая, что при этом dl ↑↓ F, получаем:
Решение. В астрономических системах потенциальную энергию тела принято вычислять относительно бесконечно удаленной точки М 0 . В этом случае, выполняя проход по радиусу от точки М (т. е. от радиуса r) до бесконечности (рис. 4.10) и учитывая, что при этом dl ↑↓ F, получаем: .
.


