
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угловое (центростремительное) ускорение
Покажем. что частица, двигаясь по окружности радиусом R с постоянной скоростью υ, испытывает постоянное по величине и всегда направленное к центру окружности О ускорение а ц.с = υ2 / R, (2.4) которое называется центростремительным. По определению, ускорение а = При равномерном движении по окружности скорость частицы υ хотя и постоянна по величине, но всё время меняется по направлению. А это означает, что отношение Δ υ / Δ t ≠ 0. Вычислим его.
а = При Δ t → 0, с учётом (2.3), а = υ ω = ω2 R, что эквивалентно (2.4), если учесть, что υ = ω R.
а ц.с = Неравномерное движение по окружности Если движение частицы по окружности неравномерное, то наряду с центростремительным ускорением (2.6), связанным с изменением вектора скорости υ по направлению, появляется и касательное, или тангенциальное ускорение а τ , связанное с изменением вектора υ по величине: а τ =
а = Период и частота При равномерном движении частицы по окружности вводятся понятия периода и частоты. Определение 1. Время Т, за которое частица совершает один оборот, называется периодом движения частицы по окружности: Т = Определение 2. Величина, обратная периоду, или число оборотов частицы за единицу времени, называется частотой f её движения по окружности: f = Таким образом, ω = 2π f = 2π /T.
~~~~~~~~~~~~~~~~~~~~~
ЗАКОНЫ НЬЮТОНА Задачей кинематики является описание движения тел по различным траекториям и не затрагивается вопрос о причинах, или силах, вызывающих это движение. Раздел «Законы Ньютона» открывает более обширную часть механики, называемую «Динамикой», где изучается влияние различных сил на характер движения тел, а также общие законы, которым подчиняются системы взаимодействующих тел в пространстве. Понятие силы В разд. 1 были даны понятия массы, времени и длины как первичные и формально не определяемые, а вводимые через эталоны. Эталона силы нет, формально она также не определяется. Её можно ввести лишь описательно, как некоторую меру взаимодействия тел, приводящую либо к изменению характера их движения, либо к их деформациям, как некоторый эквивалент трёх различных фундаментальных взаимодействий: ядерного, электромагнитного и гравитационного. Последнее означает следующее. Например, тело неподвижно лежит на столе. При этом оно участвует в двух взаимодействиях: гравитационном − со стороны Земли и упругом, которое по существу является электромагнитным, − со стороны поверхности стола. Тело неподвижно, значит эти два взаимодействия в чём-то компенсируют друг друга, хотя их природа совершенно различна. Вот это общее и называют силой, с которой Земля и стол действуют на тело. Сила F является величиной векторной, т. е. она описывается не одним числом, как скаляры, а тройкой чисел − компонентами: F = { Fx, Fy, Fz }, задающими её направление. Корень квадратный из суммы квадратов компонент даёт модуль этого вектора, или величину силы F: | F | ≡ F = Для силы F справедлив принцип суперпозиции: если к телу приложено несколько сил F k, то результирующая сила F равна векторной сумме сил F k:
В частности, две силы складываются по правилу параллелограмма (рис. 3.1): В мегамире основной силой является гравитационная
В макромире основная сила − электромагнитная, которая проявляется в различных формах: сухое и вязкое трение, упругость, чисто кулоновское или чисто магнитное взаимодействие зарядов. Третий закон Ньютона Третий закон Ньютона утверждает следующее: если тело 1 действует на тело 2 с силой F 21 , то тело 2 действует на тело 1 с такой же по величине, но противоположно направленной силой F 12 (рис. 3.2):
F 12 = − F 21 (сила действия равна силе противодействия), причём эти силы имеют одну природу, т. е., например, если одна сила гравитационная, то и другая тоже; если одна кулоновская, то другая тоже кулоновская.
|
||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.251.37 (0.008 с.) |
 . (2.5)
. (2.5) Пусть за малое время Δ t частица из точки М сместилась по окружности на угол Δφ. На рис. 2.8,а показаны векторы скорости в моменты t и (t+ Δ t). Чтобы найти вектор Δ υ = υ (t + Δ t) − υ (t) для его подстановки в (2.5), надо векторы υ (t) и υ (t + Δ t) привести к одной точке, как показано на рис. 2.8, б. И тогда сразу видно, что при малом угле Δφ величина Δυ = υ Δφ. Следовательно, при постоянной по величине скорости υ для ускорения (тоже по абсолютной величине) получаем:
Пусть за малое время Δ t частица из точки М сместилась по окружности на угол Δφ. На рис. 2.8,а показаны векторы скорости в моменты t и (t+ Δ t). Чтобы найти вектор Δ υ = υ (t + Δ t) − υ (t) для его подстановки в (2.5), надо векторы υ (t) и υ (t + Δ t) привести к одной точке, как показано на рис. 2.8, б. И тогда сразу видно, что при малом угле Δφ величина Δυ = υ Δφ. Следовательно, при постоянной по величине скорости υ для ускорения (тоже по абсолютной величине) получаем: .
. Из рис. 2.8,б видно, что вектор Δ υ всегда направлен к центру окружности, следовательно, ускорение частицы также направлено к центру (рис. 2.9), и поэтому оно называется центростремительным:
Из рис. 2.8,б видно, что вектор Δ υ всегда направлен к центру окружности, следовательно, ускорение частицы также направлено к центру (рис. 2.9), и поэтому оно называется центростремительным: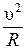 = ω2 R. (2.6)
= ω2 R. (2.6) .
. Величина ε =
Величина ε =  называется угловым ускорением. Полное ускорение частицы будет векторной суммой: а = а ц.с + а τ . Для модуля полного ускорения получаем (рис. 2.10):
называется угловым ускорением. Полное ускорение частицы будет векторной суммой: а = а ц.с + а τ . Для модуля полного ускорения получаем (рис. 2.10): .
. .
.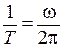 .
. .
. F = ∑ F k.
F = ∑ F k. ,
, Существенно, что эти силы приложены к разным телам и потому их складывать, вообще говоря, нельзя.
Существенно, что эти силы приложены к разным телам и потому их складывать, вообще говоря, нельзя.


