
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задач линейного программирования графическим методом,Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Решетите задачи линейного программирования по математической модели графическим методом,
1. В суточный рацион включают два продукта питания П1 и П2, причем продукта П1 должно войти в дневной рацион не более 200 ед. Стоимость 1 ед. продукта П1 составляет 2 р., продукта П2 — 4р. Содержание питательных веществ в 1 ед. продукта, минимальные нормы потребления указаны в табл. 20.2. Определить оптимальный рацион питания, стоимость которого будет наименьшей.
Составить план производства, обеспечивающий фирме наибольший доход. 3. Обработка деталей А и В может производиться на трех станках, причем каждая деталь должна последовательно обрабатываться на каждом из станков. Прибыль от реализации детали А — 100 р., детали В — 160 р. Исходные данные приведены в табл. 20.4. Определить производственную программу, максимизирующую прибыль при условии: спрос на деталь А - не менее 300 шт., на деталь В - не более 200 шт. 3. Индивидуальные задания.
Решение задач линейного программирования Симплекс методом, УПРАЖНЕНИЯ
1. L() = x 1 — 3 x 2 — 5 x 3 — х 4 → max при ограничениях:
2. L() = x 1 + 2 x 2 + 3 x 3 → min при ограничениях:
при ограничениях:
4. L() = 3 x 1 + x 2 + 2 x 3 → min при ограничениях:
5. L() = x 1 + х 2 + x 3 → max при ограничениях:
6. L() = x 1 + 2 х 2 + 2 х 3 → min при ограничениях:
7. L() = 3 x 1 + x 2 + x 3 + x 4 → max при ограничениях:
8. L() = x 1 - 5 x 2 – x 3 → max
9. L() = x 1 + х 2 + x 3 + x 4 → min при ограничениях:
10. L() = 3 x 1 + 5 x 2 + 4 x 3 → max при ограничениях:
11. Механический завод при изготовлении двух типов деталей использует токарное, фрезерное и сварочное оборудование. При этом обработку каждой детали можно вести двумя различными технологическими способами. Необходимые исходные данные приведены в табл. 21.9.
Определить оптимальную структуру товарооборота, обеспечивающую фирме максимальную прибыль. 13. Фирма выпускает четыре пользующихся спросом изделия, причем месячная программа выпуска составляет 10 изделий типа 1 и 3, 200 изделий типа 2 и 120 изделий типа 4. Нормы затрат сырья на единицу различных типов изделий приведены в табл. 21.11.
Определить, является ли месячная программа выпуска изделий оптимальной, и если нет, то определить оптимальную месячную программу и дополнительный доход, который фирма может при этом получить. 14. Металлургический завод из металлов A 1, A 2, А 3 может выпускать сплавы B 1, В 2, В 3. В течение планируемого периода завод должен освоить не менее 640 т металла A 1 и 800 т металла А 2, при этом металла А 3 может быть израсходовано не более 860 т. Определить минимальные затраты, если данные о нормах расхода и себестоимость даны в табл. 21.12.
По этим исходным данным решить следующие задачи: 1) определить оптимальный ассортимент, максимизирующий товарную продукцию предприятия; 2) приняв условие, что количество тканей трех артикулов находится в отношении 2:1:3, определить, какое максимальное количество комплектов ткани может выпустить предприятие; 3) определить оптимальный ассортимент, максимизирующий доход предприятия, если цена 1 м ткани составляет 8, 5 и 15 усл. ед. соответственно; 4) решить задачу (1) при условии, что станки 1-го типа ткань первого артикула не производят. ***
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 1901; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.209.231 (0.01 с.) |

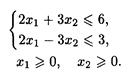



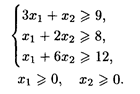



 2. Составить математическую модель задачи и решить ее графическим способом
2. Составить математическую модель задачи и решить ее графическим способом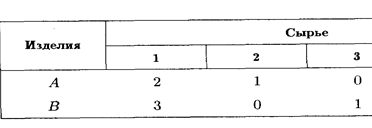 2. Фирма выпускает изделия двух типов: А и В. При этом используется сырье четырех видов. Расход сырья каждого вида на изготовление единицы продукции и запасы сырья заданы в таблице. Продолжите ее заполнение.
2. Фирма выпускает изделия двух типов: А и В. При этом используется сырье четырех видов. Расход сырья каждого вида на изготовление единицы продукции и запасы сырья заданы в таблице. Продолжите ее заполнение. Запасы сырья 1-го вида составляют 21 ед., 2-го вида — 4 ед., 3-го вида — 6 ед. и 4-го вида — 10 ед. Выпуск одного изделия типа А приносит доход 300 р., одного изделия типа В — 200р.
Запасы сырья 1-го вида составляют 21 ед., 2-го вида — 4 ед., 3-го вида — 6 ед. и 4-го вида — 10 ед. Выпуск одного изделия типа А приносит доход 300 р., одного изделия типа В — 200р.
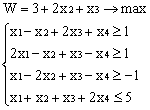
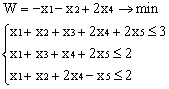
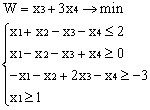











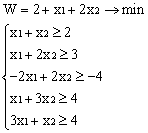
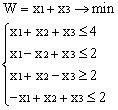













 Решить следующие задачи симплексным методом.
Решить следующие задачи симплексным методом.
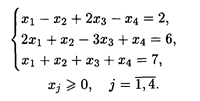 3. L() = —2 x 1 — x 2 + x 3 + x 4 → max
3. L() = —2 x 1 — x 2 + x 3 + x 4 → max




 при ограничениях:
при ограничениях:
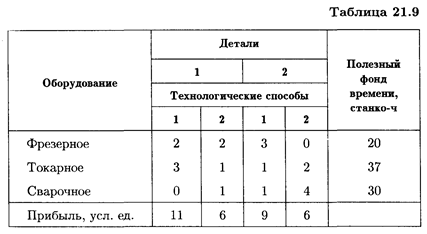
 Составить оптимальный план загрузки оборудования, обеспечивающий заводу максимальную прибыль.
Составить оптимальный план загрузки оборудования, обеспечивающий заводу максимальную прибыль. 12. Торговая фирма для продажи товаров трех видов использует ресурсы: время и площадь торговых залов. Затраты ресурсов на продажу одной партии товаров каждого вида даны в табл. 21.10. Прибыль, получаемая от реализации одной партии товаров 1-го вида, — 5 усл. ед., 2-го вида — 8 усл. ед., 3-го вида — 6 усл. ед.
12. Торговая фирма для продажи товаров трех видов использует ресурсы: время и площадь торговых залов. Затраты ресурсов на продажу одной партии товаров каждого вида даны в табл. 21.10. Прибыль, получаемая от реализации одной партии товаров 1-го вида, — 5 усл. ед., 2-го вида — 8 усл. ед., 3-го вида — 6 усл. ед. Прибыль от реализации изделий типа 1 равна 6 усл. ед., изделий типа 2 — 2 усл. ед., изделий типа 3 — 2,5 усл. ед. и изделий типа 4 — 4 усл. ед.
Прибыль от реализации изделий типа 1 равна 6 усл. ед., изделий типа 2 — 2 усл. ед., изделий типа 3 — 2,5 усл. ед. и изделий типа 4 — 4 усл. ед. 15. Ткань трех артикулов производится на ткацких станках двух типов с различной производительностью. Для изготовления ткани используются пряжа и красители. В табл. 21.13 указаны мощности станков в тысячах станко-часов, ресурсы пряжи и красителей в 1000 кг, производительности станков в метрах за час, нормы расхода пряжи и краски в килограммах на 1000 м и цена 1 м ткани.
15. Ткань трех артикулов производится на ткацких станках двух типов с различной производительностью. Для изготовления ткани используются пряжа и красители. В табл. 21.13 указаны мощности станков в тысячах станко-часов, ресурсы пряжи и красителей в 1000 кг, производительности станков в метрах за час, нормы расхода пряжи и краски в килограммах на 1000 м и цена 1 м ткани.


