
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 2. Детерминированные задачиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Раздел 2. Детерминированные задачи Тема 2.1. Линейное программирование 1.Общий вид задач линейного программирования. 2. Основная задача линейного программирования. 3. Графический метод решения задач линейного программирования 4 Симплекс-метод решения задач линейного программирования 5. Практические занятия. 1.Решение задач линейного программирования графическим методом, симплекс методом. 2. Нахождение начального решения транспортной задачи. 3. Решение транспортной задачи методом потенциалов. Приложения. 1. Решение систем m линейных неравенств с двумя переменными *** Основная задача линейного программирования. Определение. Линейное программирование (ЛП)— наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения. Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений. Определение. Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи. В общем виде математическая модель задачи линейного программирования (ЛП) записывается как
при ограничениях:
где xj — неизвестные; aij, bi, cj — заданные постоянные величины. Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств. Математическая модель в более краткой записи имеет вид
при ограничениях:
Определение. Допустимым решением (планом) задачи линейного программирования называется вектор = (x 1, x 2,..., xп), удовлетворяющий системе ограничений. Множество допустимых решений образует область допустимых решений (ОДР). Определение. Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным решением задачи линейного программирования и обозначается опт. Базисное допустимое решение (х 1, х 2 ,..., x r, 0, …, 0) является опорным решением, где r — ранг системы ограничений. Математическая модель задачи ЛП может быть канонической и неканонической. Определение. 1. Если все ограничения системы заданы уравнениями и переменные xj неотрицательные, то такая модель задачи называется канонической. 2. Если хотя бы одно ограничение является неравенством, то модель задачи ЛП является неканонической. Чтобы перейти от неканонической модели к канонической, необходимо в каждое неравенство ввести балансовую переменную xn+i. Если знак неравенства ≤, то балансовая переменная вводится со знаком плюс, если знак неравенства ≥, то — минус. В целевую функцию балансовые переменные не вводятся. Алгоритм составления математической модели задачи ЛП: ~ ввести обозначения переменных; ~ исходя из цели экономических исследований, составить целевую функцию; ~ учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений.
Алгоритм решения задач 1. Находим область допустимых решений системы ограничений задачи. 2. Строим вектор. 3. Проводим линию уровня L 0, которая перпендикулярна. 4. Линию уровня перемещаем по направлению вектора для задач на максимум и в направлении, противоположном, для задач на минимум. Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допустимых решений. Эта точка, определяющая единственное решение задачи ЛП, и будет точкой экстремума. Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача ЛП будет иметь бесчисленное множество решений. Говорят, что такая задача ЛП имеет альтернативный оптимум, и ее решение находится по формуле:
Задача ЛП может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми.
Пример 3. Выбор оптимального варианта выпуска изделий Фирма выпускает 2 вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в таблице. Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное мороженное, но не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 р., шоколадного — 14 р. Какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным? Решение. Обозначим: x 1 - суточный объем выпуска сливочного мороженого, кг; x 2 — суточный объем выпуска шоколадного мороженого, кг. Составим математическую модель задачи. Цены на мороженное известна: соответственно 16руб и 14руб., поэтому целевая функция будет иметь вид:
Установим ограничения по молоку для мороженного. Расход его на сливочное мороженное - 0,8кг, на шоколадное - 0,5кг. Запас молок 400кг. Поэтому первое неравенство будет иметь вид: 0,8х1+ 0,5х2 ≤400 – первое неравенство – ограничение. Аналогично составляются остальные неравенства.
Фигура OABDEF — область допустимых решений. Строим вектор (16; 14). Линия уровня L 0 задается уравнением 16x1+14x2=Const. Выбираем любое число, например число 0, тогда 16x1+14x2=0. На рисунке для линии L0 выбрано некоторое положительное число, не равное нулю. Все линии уровня параллельны между собой. Вектор нормаль линии уровня.
Решая систему, получим координаты точки D (312,5; 300), в которой и будет оптимальное решение, т.е.
при этом
Таким образом, фирма должна выпускать в сутки 312,5 кг сливочного мороженого и 300 кг шоколадного мороженого, при этом доход от реализации составит 9 200 р. Пример 4. Решить задачу примера 1(столы и стулья). Математическая модель ее имеет вид:
Целевая функция: 45 Х1 + 80 Х2 → max Ограничения по материалу: 5 Х1 + 20 Х2 ≤ 400 Ограничения по труду: 10 Х1 + 15 Х2 ≤ 450, Х1 ≥ 0, Х2 ≥ 0. По горизонтальной оси откладывается значения Х1, а по вертикальной оси - значения Х2. Строим фигуру, ограниченную неравенствами, получим множество возможных значений объемов выпуска стульев и столов (Х1, Х2 ), или, в других терминах, множество А, задающее ограничения на параметр управления в общей оптимизационной задаче, представляет собой пересечение двух треугольников, т.е. выпуклый четырехугольник, показанный на рис.3 Три его вершины очевидны - это (0,0), (45,0) и (0,20). Четвертая - это пересечение двух прямых - границ треугольников на рис.1 и рис.2, т.е. решение системы уравнений: 5 Х1 + 20 Х2 = 400 и 10 Х1 + 15 Х2 = 450 есть четвертая вершина четырехугольника - это (24, 14). Надо найти максимум линейной функции на выпуклом многоугольнике. (В общем случае линейного программирования - максимум линейной функции на выпуклом многограннике, лежащем в конечномерном линейном пространстве.) Основная идея линейного программирования состоит в том, что максимум достигается в вершинах многоугольника. В общем случае - в одной вершине, и это - единственная точка максимума. В частном - в двух, и тогда отрезок, их соединяющий, тоже состоит из точек максимума.
Таким образом, оптимальный выпуск: 24 стула и 14 столов. Пример 5. Продолжить решение задачи примера 2. (Кондитерская фабрика…) 4. Симплекс-метод решения задач линейного программирования Основное содержание симплексного метода Для решения задачи симплекс методом необходимо: 1. Указать способ нахождения оптимального опорного решения 2. Указать способ перехода от одного опорного решения к другому, на котором значение целевой функции будет ближе к оптимальному, т.е. указать способ улучшения опорного решения 3. Задать критерии, которые позволяют своевременно прекратить перебор опорных решений на оптимальном решении или сдать заключение об отсутствии оптимального решения. Алгоритм симплексного метода решения задач линейного программирования 1. Привести задачу к каноническому виду 2. Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решение, в виду несовместимости системы ограничений) 3. Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода 4. Если выполняется признак единственности оптимального решения, то решение задачи заканчивается 5. Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения
Пример1 Решить симплексным методом задачу: Решение: Приводим задачу к каноническому виду.
Находим начальное опорное решение. Для этого свободные (неразрешенные) переменные приравниваем к нулю х1 = х2 = х3 = 0. Получаем опорное решение Х1 = (0,0,0,24,30,6) с единичным базисом Б1 = (А4, А5, А6).
Где: Cб = (с1, с2,..., сm) — вектор коэффициентов целевой функции при базисных переменных Xk = (x1k, x2k,..., xmk) — вектор разложения соответствующего вектора Ак по базису опорного решения Ск — коэффициент целевой функции при переменной хк.
Сверху над таблицей для удобства вычислений оценок записываются коэффициенты целевой функции. В первом столбце "Б" записываются векторы, входящие в базис опорного решения. Порядок записи этих векторов соответствует номерам разрешенных неизвестных в уравнениях ограничениях. Во втором столбце таблицы "Сб" записываются коэффициенты целевой функции при базисных переменных в том же порядке. При правильном расположении коэффициентов целевой функции в столбце "Сб" оценки единичных векторов, входящих в базис, всегда равных нулю. В последней строке таблицы с оценками Δk в столбце "А0" записываются значения целевой функции на опорном решении Z(X1). Начальное опорное решение не является оптимальным, так как в задаче на максимум оценки Δ1 = -2, Δ3= -9 для векторов А1 и А3 отрицательные. По теореме об улучшении опорного решения, если в задаче на максимум хотя бы один вектор имеет отрицательную оценку, то можно найти новое опорное решение, на котором значение целевой функции будет больше. Определим, введение, какого из двух векторов приведет к большему приращению целевой функции. Приращение целевой функции находится по формуле:. Вычисляем значения параметра θ01 для первого и третьего столбцов по формуле: Получаем θ01 = 6 при l = 1, θ03 = 3 при l = 1 (таблица 26.1). Находим приращение целевой функции при введении в базис первого вектора ΔZ1 = — 6·(- 2) = 12, и третьего вектора ΔZ3 = — 3·(- 9) = 27. Следовательно, для более быстрого приближения к оптимальному решению необходимо ввести в базис опорного решения вектор А3 вместо первого вектора базиса А6, так как минимум параметра θ03 достигается в первой строке (l = 1).
Это решение не является оптимальным, так как вектор А2 имеет отрицательную оценку Δ2 = — 6. Для улучшение решения необходимо ввести вектор А2 в базис опорного решения.
Это решение является единственным оптимальным, так как для всех векторов, не входящих в базис оценки положительные Δ1 = 7/2, Δ4 = 2, Δ6 = 7/2. Ответ: max Z(X) = 201 при Х = (0,7,10,0,63). Предприятия
При первом способе производства предприятие выпускает за один месяц 3 тыс. изделий, при втором — 4 тыс. изделий. Сколько месяцев должно работать предприятие каждым из этих способов, чтобы при наличных ресурсах обеспечить максимальный выпуск продукции? Решение. Составим математическую модель задачи. Обозначим: x 1 — время работы предприятия первым способом, x 2 — время работы предприятия вторым способом.
при ограничениях:
Приведем задачу к каноническому виду:
при ограничениях:
Составляем симплексную таблицу 1-го шага (табл. 21.3).
Получим
В индексной строке имеется одна отрицательная оценка. Полученное решение можно улучшить. Ключевым элементом является (1/2). Составляем симплексную таблицу 3-го шага (табл. 21.5).
Таким образом, по первому способу предприятие должно работать два месяца, по второму — один месяц, при этом максимальный выпуск продукции составит 10 тыс. ед. Альтернативный оптимум При решении задач линейного программирования симплексным методом критерием оптимальности является условие Δ j ≥ 0 для задач на максимум и условие Δ j < 0 для задач на минимум. Если на каком-то шаге окажется, что хотя бы одна оценка свободной переменной Δ j = 0, а все остальные Δ j > 0 для задач на максимум (Δ j < 0 для задач на минимум), то, приняв в качестве ключевого столбца столбец, где Δ j = 0, и найдя новое оптимальное решение, заметим, что значение целевой функции при этом не изменится. Говорят, что в этом случае задача имеет альтернативный оптимум. Критерием альтернативного оптимума при решении задач симплексным методом является равенство нулю хотя бы одной оценки свободной переменной (Δ j = 0). Если только одна оценка свободной переменной равна нулю, то решение находится по формуле
Если две оценки и более, например S, свободных переменных равны нулю, то оптимальное решение определяется по формуле
В задачах, имеющих альтернативный оптимум, возникает возможность включения в ее модель других критериев эффективности.
при ограничениях:
Решение. Составим симплексную таблицу (табл. 21.6). В индексной строке имеется одна положительная оценка. Полученное решение можно улучшить. Ключевым элементом является (4). Составляем симплексную таблицу 2-го шага (табл. 21.7). Получаем
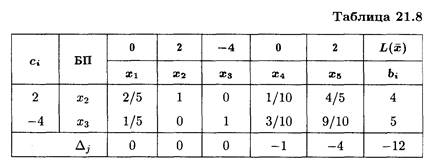
Так как Δ2 = 0, то задача имеет альтернативный оптимум. Найдем еще одно оптимальное решение, введя вместо базисной переменной х 1 свободную переменную х 2 (табл. 21.8). Получаем
Найдем координаты оптимального решения задачи:
Давая t значения из [0,1], получим различные опт, при которых L() = -12. Практические занятия. УПРАЖНЕНИЯ
1. L() = x 1 — 3 x 2 — 5 x 3 — х 4 → max при ограничениях:
2. L() = x 1 + 2 x 2 + 3 x 3 → min при ограничениях:
при ограничениях:
4. L() = 3 x 1 + x 2 + 2 x 3 → min при ограничениях:
5. L() = x 1 + х 2 + x 3 → max при ограничениях:
6. L() = x 1 + 2 х 2 + 2 х 3 → min при ограничениях:
7. L() = 3 x 1 + x 2 + x 3 + x 4 → max при ограничениях:
8. L() = x 1 - 5 x 2 – x 3 → max
9. L() = x 1 + х 2 + x 3 + x 4 → min при ограничениях:
10. L() = 3 x 1 + 5 x 2 + 4 x 3 → max при ограничениях:
11. Механический завод при изготовлении двух типов деталей использует токарное, фрезерное и сварочное оборудование. При этом обработку каждой детали можно вести двумя различными технологическими способами. Необходимые исходные данные приведены в табл. 21.9.
Определить оптимальную структуру товарооборота, обеспечивающую фирме максимальную прибыль. 13. Фирма выпускает четыре пользующихся спросом изделия, причем месячная программа выпуска составляет 10 изделий типа 1 и 3, 200 изделий типа 2 и 120 изделий типа 4. Нормы затрат сырья на единицу различных типов изделий приведены в табл. 21.11.
Определить, является ли месячная программа выпуска изделий оптимальной, и если нет, то определить оптимальную месячную программу и дополнительный доход, который фирма может при этом получить. 14. Металлургический завод из металлов A 1, A 2, А 3 может выпускать сплавы B 1, В 2, В 3. В течение планируемого периода завод должен освоить не менее 640 т металла A 1 и 800 т металла А 2, при этом металла А 3 может быть израсходовано не более 860 т. Определить минимальные затраты, если данные о нормах расхода и себестоимость даны в табл. 21.12.
По этим исходным данным решить следующие задачи: 1) определить оптимальный ассортимент, максимизирующий товарную продукцию предприятия; 2) приняв условие, что количество тканей трех артикулов находится в отношении 2:1:3, определить, какое максимальное количество комплектов ткани может выпустить предприятие; 3) определить оптимальный ассортимент, максимизирующий доход предприятия, если цена 1 м ткани составляет 8, 5 и 15 усл. ед. соответственно; 4) решить задачу (1) при условии, что станки 1-го типа ткань первого артикула не производят. *** Приложения Решение систем m линейных неравенств с двумя переменными Дана система т линейных неравенств с двумя переменными
Знаки некоторых или всех неравенств могут быть ≥. Рассмотрим первое неравенство в системе координат Х 1 ОХ 2. Построим прямую
которая является граничной прямой. Эта прямая делит плоскость на две полуплоскости 1 и 2. Полуплоскость 1 содержит начало координат, полуплоскость 2 не содержит начала координат. Для определения, по какую сторону от граничной прямой расположена заданная полуплоскость, надо взять произвольную точку на плоскости (лучше начало координат) и подставить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, если не справедливо, то в противоположную от точки сторону. Направление полуплоскости на рисунках показываем стрелкой. Определение. Решением каждого неравенства системы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Определение. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы (ОР). Определение. Область решения системы, удовлетворяющая условиям неотрицательности (xj ≥ 0, j =), называется областью неотрицательных, или допустимых, решений (ОДР). Если система неравенств совместна, то ОР и ОДР могут быть многогранником, неограниченной многогранной областью или одной точкой. Если система неравенств несовместна, то ОР и ОДР — пустое множество. Пример 1. Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР
Решение.. Найдем ОР первого неравенства: х 1 + 3 x 2 ≥ 3. Построим граничную прямую х 1 +3 x 2 – 3 = 0.Подставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решением неравенства (19.1) является полуплоскость, не содержащая точку (0,0).
Точку В найдем как точку пересечения прямых Из системы получим B (5/3, 10/3). Аналогично найдем координаты точек С и D: С (11/4; 9/14), D (3/10; 21/10). Пример 2. Найти ОР и ОДР системы неравенств
Р
Решение.. Построим прямые и определим решения неравенств. ОР и ОДР являются неограниченные многогранные области ACFM и ABDEKM соответственно.
Пример 4. Найти OP и ОДР системы неравенств
Решение. Построив прямые, найдем решения неравенств системы. ОР и ОДР несовместны. УПРАЖНЕНИЯ Найти ОР и ОДР систем неравенств
Найти ОР и ОДР систем неравенств
Найти ОР и ОДР систем неравенств
Раздел 2. Детерминированные задачи
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 1019; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |





 где 0 ≤ t ≤ 1, 1 и 2 — оптимальные решения в угловых точках ОДР.
где 0 ≤ t ≤ 1, 1 и 2 — оптимальные решения в угловых точках ОДР. 5. Находим координаты точки экстремума и значение целевой функции в ней.
5. Находим координаты точки экстремума и значение целевой функции в ней.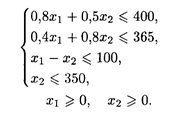

 В результате получится система неравенств. что область решения каждого неравенства. Это можно сделать, подставив в каждое из неравенств координаты точки О(0:0). В результате получим:
В результате получится система неравенств. что область решения каждого неравенства. Это можно сделать, подставив в каждое из неравенств координаты точки О(0:0). В результате получим: Перемещаем линию уровня по направлению вектора. Точкой выхода L 0 из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, заданных уравнениями:
Перемещаем линию уровня по направлению вектора. Точкой выхода L 0 из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, заданных уравнениями: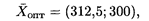

 Целевая функция 45 Х1 + 80 Х2 принимает минимальное значение, равное 0, в вершине (0,0). При увеличении аргументов эта функция увеличивается. В вершине (24,14) она принимает значение 2200. При этом прямая 45 Х1 + 80 Х2 = 2200 проходит между прямыми ограничений 5 Х1 + 20 Х2 = 400 и 10 Х1 + 15 Х2 = 450, пересекающимися в той же точке. Отсюда, как и из непосредственной проверки двух оставшихся вершин, вытекает, что максимум целевой функции, равный 2200, достигается в вершине (24,14).
Целевая функция 45 Х1 + 80 Х2 принимает минимальное значение, равное 0, в вершине (0,0). При увеличении аргументов эта функция увеличивается. В вершине (24,14) она принимает значение 2200. При этом прямая 45 Х1 + 80 Х2 = 2200 проходит между прямыми ограничений 5 Х1 + 20 Х2 = 400 и 10 Х1 + 15 Х2 = 450, пересекающимися в той же точке. Отсюда, как и из непосредственной проверки двух оставшихся вершин, вытекает, что максимум целевой функции, равный 2200, достигается в вершине (24,14).
 Для этого в левую часть первого ограничения-неравенства вводим дополнительную переменную x6 с коэффициентом +1. В целевую функцию переменная x6 входит с коэффициентом ноль (т.е. не входит).
Для этого в левую часть первого ограничения-неравенства вводим дополнительную переменную x6 с коэффициентом +1. В целевую функцию переменная x6 входит с коэффициентом ноль (т.е. не входит). Вычисляем оценки разложений векторов условий по базису опорного решения по формуле: Δk = CбXk — ck ,
Вычисляем оценки разложений векторов условий по базису опорного решения по формуле: Δk = CбXk — ck ,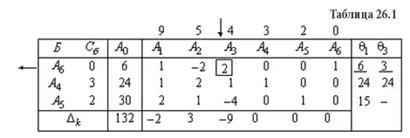 Оценки векторов входящих в базис всегда равны нулю. Опорное решение, коэффициенты разложений и оценки разложений векторов условий по базису опорного решения записываются в симплексную таблицу 26.1
Оценки векторов входящих в базис всегда равны нулю. Опорное решение, коэффициенты разложений и оценки разложений векторов условий по базису опорного решения записываются в симплексную таблицу 26.1
 Производим преобразование Жордана с элементом Х13 = 2, получаем второе опорное решение Х2 = (0,0,3,21,42,0) с базисом Б2 = (А3, А4, А5). (таблица 26.2)
Производим преобразование Жордана с элементом Х13 = 2, получаем второе опорное решение Х2 = (0,0,3,21,42,0) с базисом Б2 = (А3, А4, А5). (таблица 26.2) Определяем номер вектора, выводимого из базиса. Для этого вычисляем параметр θ02 для второго столбца, он равен 7 при l = 2. Следовательно, из базиса выводим второй вектор базиса А4. Производим преобразование Жордана с элементом х22 = 3, получаем третье опорное решение Х3 = (0,7,10,0,63,0) Б2 = (А3, А2, А5) (таблица 26.3).
Определяем номер вектора, выводимого из базиса. Для этого вычисляем параметр θ02 для второго столбца, он равен 7 при l = 2. Следовательно, из базиса выводим второй вектор базиса А4. Производим преобразование Жордана с элементом х22 = 3, получаем третье опорное решение Х3 = (0,7,10,0,63,0) Б2 = (А3, А2, А5) (таблица 26.3). Предприятие располагает тремя производственными ресурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя различными способами. Расход ресурсов за один месяц и общий ресурс при каждом способе производства даны в табл. 21.2 (в усл. ед.).
Предприятие располагает тремя производственными ресурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя различными способами. Расход ресурсов за один месяц и общий ресурс при каждом способе производства даны в табл. 21.2 (в усл. ед.). Математическая модель имеет вид
Математическая модель имеет вид 


 Получим решение:
Получим решение: В индексной строке Δ j имеются две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве ключевого столбца следует принять столбец базисной переменной х 2, а за ключевую строку взять строку переменной x 3, где min (4/2,3/l, 8/1) = min (2, 3, 8) = 2.
В индексной строке Δ j имеются две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве ключевого столбца следует принять столбец базисной переменной х 2, а за ключевую строку взять строку переменной x 3, где min (4/2,3/l, 8/1) = min (2, 3, 8) = 2. Ключевым элементом является (2). Вводим в столбец базисной переменной х 2, выводим х 3. Составляем симплексную таблицу 2-го шага (табл. 21.4).
Ключевым элементом является (2). Вводим в столбец базисной переменной х 2, выводим х 3. Составляем симплексную таблицу 2-го шага (табл. 21.4).

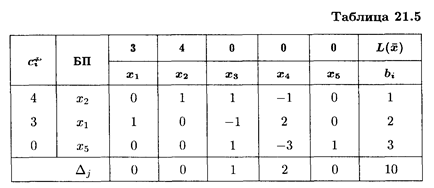 Все оценки свободных переменных Δ j ≥ 0, следовательно, найденное опорное решение является оптимальным:
Все оценки свободных переменных Δ j ≥ 0, следовательно, найденное опорное решение является оптимальным: где 0 ≤ t ≤ 1.
где 0 ≤ t ≤ 1.

 Пример. Дана задача линейного программирования
Пример. Дана задача линейного программирования






 Решить следующие задачи симплексным методом.
Решить следующие задачи симплексным методом.
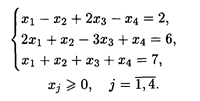 3. L() = —2 x 1 — x 2 + x 3 + x 4 → max
3. L() = —2 x 1 — x 2 + x 3 + x 4 → max




 при ограничениях:
при ограничениях:
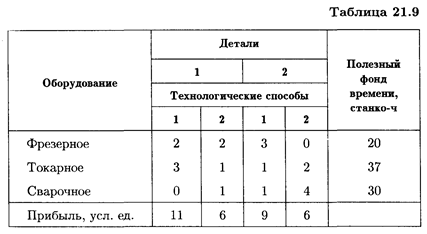
 Составить оптимальный план загрузки оборудования, обеспечивающий заводу максимальную прибыль.
Составить оптимальный план загрузки оборудования, обеспечивающий заводу максимальную прибыль. 12. Торговая фирма для продажи товаров трех видов использует ресурсы: время и площадь торговых залов. Затраты ресурсов на продажу одной партии товаров каждого вида даны в табл. 21.10. Прибыль, получаемая от реализации одной партии товаров 1-го вида, — 5 усл. ед., 2-го вида — 8 усл. ед., 3-го вида — 6 усл. ед.
12. Торговая фирма для продажи товаров трех видов использует ресурсы: время и площадь торговых залов. Затраты ресурсов на продажу одной партии товаров каждого вида даны в табл. 21.10. Прибыль, получаемая от реализации одной партии товаров 1-го вида, — 5 усл. ед., 2-го вида — 8 усл. ед., 3-го вида — 6 усл. ед. Прибыль от реализации изделий типа 1 равна 6 усл. ед., изделий типа 2 — 2 усл. ед., изделий типа 3 — 2,5 усл. ед. и изделий типа 4 — 4 усл. ед.
Прибыль от реализации изделий типа 1 равна 6 усл. ед., изделий типа 2 — 2 усл. ед., изделий типа 3 — 2,5 усл. ед. и изделий типа 4 — 4 усл. ед. 15. Ткань трех артикулов производится на ткацких станках двух типов с различной производительностью. Для изготовления ткани используются пряжа и красители. В табл. 21.13 указаны мощности станков в тысячах станко-часов, ресурсы пряжи и красителей в 1000 кг, производительности станков в метрах за час, нормы расхода пряжи и краски в килограммах на 1000 м и цена 1 м ткани.
15. Ткань трех артикулов производится на ткацких станках двух типов с различной производительностью. Для изготовления ткани используются пряжа и красители. В табл. 21.13 указаны мощности станков в тысячах станко-часов, ресурсы пряжи и красителей в 1000 кг, производительности станков в метрах за час, нормы расхода пряжи и краски в килограммах на 1000 м и цена 1 м ткани.




 Аналогично найдем решения остальных неравенств системы. Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.
Аналогично найдем решения остальных неравенств системы. Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD. Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых Решая систему, получим А (3/7, 6/7).
Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых Решая систему, получим А (3/7, 6/7).

 Пример 3. Найти ОР и ОДР системы неравенств
Пример 3. Найти ОР и ОДР системы неравенств
 Решение. Найдем решения неравенств (19.8)-(19.10). ОР представляет неограниченную многогранную область ABC; ОДР — точка В.
Решение. Найдем решения неравенств (19.8)-(19.10). ОР представляет неограниченную многогранную область ABC; ОДР — точка В.







