Симплекс-метод, составление симплекс-таблиц

Вид сырья	Нормы затрат сырья (кг) на одно изделие	Общее количество сырья (кг
A	B	C
I
II
III
Цена одного изделия (руб.)

Изделия А, В и С могут производиться в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида.

Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.

Решение. Составим математическую модель задачи. Искомый выпуск изделий А обозначим через x1, изделий В – через, изделий С – через. Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные должны удовлетворять следующей системе неравенств:

По своему экономическому содержанию переменные могут принимать только лишь неотрицательные значения:

(31)

Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (29) требуется найти такое, при котором функция (30) принимает максимальное значение.

Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений

Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, – это неиспользуемое количество сырья I вида.

Преобразованную систему уравнений запишем в векторной форме:

Поскольку среди векторов имеются три единичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план Х=(0; 0; 0; 360; 192; 180), определяемый системой трехмерных единичных векторов которые образуют базис трехмерного векторного просранства.

Таблица 6
i	Базис	Сб	P0
			P1	P2	Р3	p4	Р5	P6
	P4
	р5
	p6
				-9	-10	-16

Составляем симплексную таблицу для I итерации (табл. 6), подсчитываем значения и проверяем исходный опорный план на оптимальность

Для векторов базиса

Как видно из таблицы 6, значения всех основных переменных равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому “плану”, при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т. е. стоимость произведенной продукции отсутствует). Этот план, конечно, не является оптимальным.

Это видно и из 4-й строки табл. 6, так как в ней имеется три отрицательных числа: и Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции.

Так, число – 9 означает, что при включении в план производства одного изделия А обеспечивается увеличение выпуска продукции на 9 руб. Если включить в план производства по одному изделию В и С, то общая стоимость изготовляемой продукции возрастет соответственно на 10 и 16 руб. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделий С. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число стоит в 4-й строке столбца вектора Р3. Следовательно, в базис введем вектор Р3. определяем вектор, подлежащий исключению из базиса. Для этого находим

Найдя число 192:6=24 мы тем самым с экономической точки зрения определили, какое количество изделий С предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие С требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделий С, которое может быть изготовлено предприятием, равно

т. е. ограничивающим фактором для производства изделий С является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия С. При этом сырье II вида будет полностью использовано.

Следовательно, вектор Р5 подлежит исключению из базиса. Столбец вектора Р3 к 2-я строка являются направляющими. Составляем таблицу для II итерации (табл. 7).

Приложения

Решение систем m линейных неравенств с двумя переменными

Дана система т линейных неравенств с двумя переменными

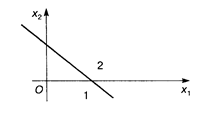
Знаки некоторых или всех неравенств могут быть ≥.

Рассмотрим первое неравенство в системе координат Х ₁ ОХ ₂. Построим прямую

которая является граничной прямой.

Эта прямая делит плоскость на две полуплоскости 1 и 2.

Полуплоскость 1 содержит начало координат, полуплос­кость 2 не содержит начала координат.

Для определения, по какую сторону от граничной прямой расположена заданная полуплоскость, надо взять произволь­ную точку на плоскости (лучше начало координат) и подста­вить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, если не справедливо, то в противоположную от точки сторону.

Направление полуплоскости на рисунках показываем стрел­кой.

Определение. Решением каждого неравенства систе­мы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.

Определение. Пересечение полуплоскостей, каждая из ко­торых определяется соответствующим неравенством системы, называется областью решения системы (ОР).

Определение. Область решения системы, удовлетворяю­щая условиям неотрицательности (x_j ≥ 0, j =), называ­ется областью неотрицательных, или допустимых, решений (ОДР).

Если система неравенств совместна, то ОР и ОДР могут быть многогранником, неограниченной многогранной облас­тью или одной точкой.

Если система неравенств несовместна, то ОР и ОДР — пус­тое множество.

Пример 1. Найти ОР и ОДР системы неравенств и опреде­лить координаты угловых точек ОДР

 

Решение.. Найдем ОР первого неравенства: х ₁ + 3 x ₂ ≥ 3. Построим граничную прямую х ₁ +3 x ₂ – 3 = 0.Под­ставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решени­ем неравенства (19.1) является полуплоскость, не содержащая точку (0,0).

Аналогично найдем решения остальных неравенств систе­мы. Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.

Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых Решая систему, получим А (3/7, 6/7).

Точку В найдем как точку пересечения прямых

Из системы получим B (5/3, 10/3). Аналогично найдем коорди­наты точек С и D: С (11/4; 9/14), D (3/10; 21/10).

Пример 2. Найти ОР и ОДР системы неравенств

 

Р

 

 

Решение.. Построим прямые и определим решения не­равенств. ОР и ОДР являются неограниченные многогранные области ACFM и ABDEKM соответственно.

Пример 3. Найти ОР и ОДР системы неравенств

 

 

Решение. Найдем решения неравенств (19.8)-(19.10). ОР представляет неограниченную многогранную область ABC; ОДР — точка В.

Пример 4. Найти OP и ОДР системы неравенств

 

 

Решение. Построив прямые, найдем решения неравенств системы. ОР и ОДР несовместны.

УПРАЖНЕНИЯ

Найти ОР и ОДР систем неравенств

 

 

 

Найти ОР и ОДР систем неравенств

 

 

Найти ОР и ОДР систем неравенств