
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние методических погрешностей на результаты измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Методическая погрешность – погрешность измерения, происходящая из-за несовершенства метода измерений. Эта погрешность может возникать из-за принципиальных недостатков используемого метода, из-за неполноты знаний о происходящих при измерении процессах, из-за неточности применяемых расчетных формул. Методическая погрешность может и должна быть оценена только самим экспериментатором с учетом конкретных условий эксперимента. Пример Оценить погрешность измерения мощности методом двух приборов (рис.2.1).
а) б) Рис.2.1. Схема измерения мощности:Iа – ток, измеряемый амперметром; Iн – ток, протекающий через сопротивление нагрузки; Iv – ток, протекающий через вольтметр; Рн - действительное значение измеряемой мощности. Измеренное значение в случае а) Р=IнU=Iн (Uн+Uа) =IнUн+IнUа=Pн+IнUа. Абсолютная погрешность Dр=Р-Рн= Pн+IнUа -Pн= IнUа. Относительная погрешность dр1=Dр/Рн = IнUа/ IнUн= Uа/ Uн =(IнRа)/(IнRн)= Rа/ Rн. dр1 ® 0 при Rа ® 0 или Rн® ¥. Измеренное значение в случае б): Р=IUн=(Iн +Iv)Uн=IнUн+IvUн=Pн+IvUн. Абсолютная погрешность Dр=Р-Рн= Pн+IvUн -Pн= IvUн. Относительная погрешность dр2=Dр/Рн = IvUн/ IнUн= Iv/ Iн=(Uн/Rv)/(Uн/Rн)= Rн/ Rv. dр2® 0 при Rн ® 0 или Rv® ¥. dр1=dр2 Þ Rн/ Rv= Rа/ Rн Þ Rн= При Rа=0,002 Ом; Rv=1000 Ом; Rн =1,41 Ом; dр=0,14%. Пример
Rv Ri
Рис.2.2.Схема измерения напряжения Оценить систематическую погрешность измерения напряжения Ux источника, обусловленную наличием внутреннего сопротивления вольтметра. Внутреннее сопротивление источника напряжения Ri =50 Oм; сопротивление вольтметра Rv =5 кОм; показание вольтметра Uизм =12,2 В. Решение Здесь Это достаточно ощутимая погрешность и ее следует учесть введением поправки. Поправка Ñ равна погрешности, взятой с обратным знаком. Ñ=0,99·10-2·12,2=+0,12 В. Ux =12,2+0,12=12,32 В. Полученная оценка имеет погрешность из-за погрешностей в определении показаний вольтметра (личная или субъективная погрешность), а также из-за инструментальной погрешности вольтметра. Эта погрешностью при введении поправки не исключается и называется неисключенным остатком систематической погрешности. Личные систематические погрешности связаны с индивидуальными особенностями наблюдателя. Для уменьшения этого вида погрешностей надо точно соблюдать правила эксплуатации средств измерений и иметь навыки работы с измерительной техникой. Задачи 1. Элемент, у которого Е = 1,5 В, а внутреннее сопротивление R0 = 0,2 Ом, замкнут на внешнее сопротивление R = 14,8 Ом. Определить, чему будет равна относительная погрешность при расчете тока в цепи, если внутренним сопротивлением элемента пренебречь. Как изменится относительная погрешность, если при прочих равных условиях внешнее сопротивление вместо 14,8 станет равным 0,3 Ом? 2. Какова относительная погрешность измерения ЭДС генератора, изображенного на рис.2.3., при измерении ее вольтметром с сопротивлением 10 кОм? Внутреннее сопротивление генератора Rя = 0,2 Ом.
Рис.2.3. Схема измерения ЭДС генератора
3. С помощью амперметра с внутренним сопротивлением RА измерено значение тока, протекающего через резистор R, подключенный к источнику напряжения с внутренним сопротивлением Ri.Определить относительную систематическую погрешность δс измерения тока, вызванную сопротивлением амперметра 4. Амперметр сопротивлением rА=0,01 Ом и вольтметр сопротивлением rV=25 Ом применяются в схеме для измерения сопротивления якоря электродвигателя. Составить схему измерения методом амперметра и вольтметра, а также определить приближенное и точное значение сопротивления и относительную погрешность, допускаемую при определении сопротивления по приближенной формуле, если наиболее вероятные значения тока и напряжения, полученные в результате повторных измерений, следующие: I=8,5 A, U=1,25 В. 5. Определить относительную погрешность измерения сопротивления последовательной обмотки возбуждения электродвигателя, если ток I=1,1 A, напряжение U=33 мВ, сопротивление амперметра 0,1 Ом, милливольтметра 10 Ом. Составить схему измерения. 6.
Для измерения сопротивления r=200 Ом используются амперметр сопротивлением rА=0,05 Ом, вольтметр сопротивлением rV=10 кОм. Какая из двух схем (рис.2.4 а и б) измерения сопротивления методом амперметра и вольтметра дает меньшую погрешность измерения? а). б). рис.2.4. Схема измерения сопротивления 7. Для определения ЭДС генератора к его зажимам присоединен вольтметр сопротивлением Rv = 1200 Ом. Внутреннее сопротивление генератора Rя= 0,6 Ом. Какую ошибку мы допускаем, считая показание вольтметра равным Э. Д. С. генератора? 8. При измерении напряжения на нагрузке сопротивлением 7 Ом вольтметр показал 13,5 В. ЭДС. источника Е = 14,2 В, а его внутреннее сопротивление R0 = 0,1 Ом. Определить абсолютную и относительную погрешности измерения. 9. По схеме амперметра и вольтметра измеряется сопротивление нагрузки rН. За измеренное значение принимается сопротивление, найденное по закону Ома. Определить, какая из схем дает большую погрешность, если известно, что ток Iн= 5 А, напряжение Uн=120 В, rv=20 кОм, rА=0,01 Ом. Составить схемы измерения. 10. При измерении сопротивления обмотки якоря методом амперметра и вольтметра применяемые приборы имели следующие показания: амперметр с пределом измерения 0,75 А - 90 делении; вольтметр с пределом измерения 7,5 В и сопротивлением 2,5 кОм - 113,5 делений. Шкалы обоих приборов имеют 150 делений. Составить схему измерения и определить сопротивление якоря. 11. В лаборатории при измерении двух сопротивлений методом амперметра и вольтметра применены: миллиамперметр с сопротивлением 10 Ом; вольтметр с сопротивлением 400 Ом. Показания приборов по схеме рис.2.4,а при измерении первого сопротивления были U1=0,7 В, I1=50 мА, а при измерении второго сопротивления соответствующие измерения дали U2=1,32 В, I2=26,5 мА; Определить значения сопротивлений и относительную погрешность измерения. 12. В лаборатории при измерении двух сопротивлений методом амперметра и вольтметра применены: миллиамперметр с сопротивлением 10 Ом; вольтметр с сопротивлением 400 Ом. Показания приборов по схеме рис.2.4,б U1=0,2 В, U2=1,05 В, токи I1=50 мА, I2=29 мА. Определить значения сопротивлений и относительную погрешность измерения.
3. Обнаружение и исключение систематических погрешностей В зависимости от характера и причин появления погрешности измерений и средств измерений делят на систематические (детерминированные) и случайные (стохастические). Различают ещё грубые погрешности и промахи. Систематическая погрешность – составляющая погрешности измерения, которая при повторении равноточных измерений неизменного размера остается постоянной или закономерно изменяется. Систематические погрешности могут быть изучены, при этом результат измерения может быть уточнен или путем внесения поправок, если числовые значения этих погрешностей определены, или путем применения таких способов измерения, которые дают возможность исключить влияние систематических погрешностей без их определения. Числовые значения систематических погрешностей определяются путем поверки средств измерений. В настоящее время, особенно после введения одного из основополагающих метрологических стандартов ГОСТ 8.009-84 “ГСИ. Основные метрологические характеристики средств измерений”, понятие “систематическая погрешность” несколько изменилось по При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей. Постоянная систематическая погрешность не устраняется при многократных измерениях. Для устранения постоянных систематических погрешностей применяют графические и специальные статистические методы. К последним относятся способ последовательных разностей, дисперсионный анализ и др. Способ последовательных разностей (критерий Аббе) применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем. Дисперсию результата измерений можно оценить двумя способами: обычным
и вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей (xi+1-xi)2
Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т.е. имела место переменная систематическая погрешность, то S2[х] дает преувеличенную оценку дисперсии результатов наблюдений. Это объясняется тем, что на S2[х] влияют вариации
является критерием для обнаружения систематических смещений центра группирования результатов наблюдений. Критическая область для этого критерия (критерия Аббе) определяется как Р(ν<νq)=q, где q=1-P – уровень значимости, Р - доверительная вероятность. Значения νq для разных уровней значимости q и числа наблюдений n приведены в таблице 3.1.
Таблица 3.1 Значения критерия Аббе
Если полученное значение критерия Аббе меньше νq ‚ при заданных q и n, то гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т.е. обнаруживается переменная систематическая погрешность результатов измерений. Пример Таблица 3.2 Результаты наблюдений
Используя способ последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений, приведенных во втором столбце табл.3.2. Для приведенного ряда результатов вычисляем: среднее арифметическое Задача Используя способ последовательных разностей, определить, присутствует ли систематическая погрешность в ряду результатов наблюдений, приведенных в табл. 3.3. Таблица 3.3 Результаты измерений
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 3272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.28.79 (0.008 с.) |


 .
.






 Ux
Ux и относительная систематическая погрешность
и относительная систематическая погрешность  .
.

 (3.1)
(3.1)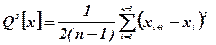 . (3.2)
. (3.2)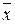 . В то же время изменения центра группирования
. В то же время изменения центра группирования  поэтому смещения
поэтому смещения  (3.3)
(3.3)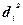

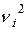
 17
17



