
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностное описание случайных погрешностей
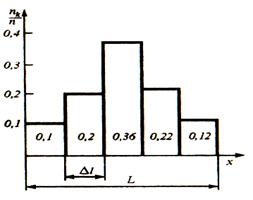
Когда при проведении в одинаковых условиях повторных измерений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Эта погрешность возникает вследствие одновременного воздействия на результат многих случайных возмущений и сама является случайной величиной. Для установления вероятностных (статистических) закономерностей появления случайных погрешностей и количественной оценки результата измерений и его случайной погрешности используются методы теории вероятностей и математической статистики. Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. В метрологии преимущественно используется дифференциальная форма – закон распределения плотности вероятностей случайной величины. Рассмотрим формирование дифференциального закона. 1. Проведем n измерений одной величины Х. 2. Получим группу наблюдений х1; х2,…,хn. 3. Расположим результаты в порядке возрастания от хmin до хmax. 4. Найдем размах ряда L=хmax - хmin. 5. Разделим размах ряда на k равных интервалов ∆l=L/k. 6. Подсчитаем количество наблюдений nk, попадающих в каждый интервал. 7. Изобразим полученные результаты графически (по оси абсцисс – значения физической величины с границами интервалов; по оси ординат – относительная частота попаданий nk/n). 8. Достроив по полученным точкам соответствующие прямоугольники, получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте. Пример. N=50 измерений.
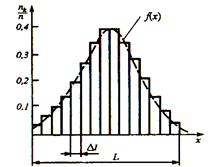
Рис.4.1. Гистограмма Если распределение случайной величины статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Следовательно, по гистограмме можно предсказывать распределение результатов измерений по интервалам. При бесконечном увеличении числа наблюдений n→∞ и бесконечном уменьшении ширины интервалов Δl→0, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую f(x), которая называется кривой плотности распределения вероятностей случайной величины, а уравнения ее описывающие дифференциальным законом распределения.
Рис.4.2. Кривая плотности распределения вероятностей Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде:
Если известен закон распределения случайной величины f(x), то вероятность Р ее попадания в интервал от х1 до х2
Числовые характеристики случайных величин вычисляются по следующим формулам: · среднее арифметическое значение исправленных результатов наблюдений
· смещенная (S*) и несмещенная (S) среднеквадратическая погрешность ряда измерений
· среднеквадратическая погрешность среднеарифметического значения
Методика проверки гипотезы о том, что результаты наблюдений распределены нормально, зависит от числа наблюдений: - если n≥50, используют критерий χ2 Пирсона; - если 15<n<50, то используют составной критерий; - если n≤15, то гипотезу не проверяют (в этом случае данная методика обработки результатов может применяться, если априорно известно, что наблюдения распределены нормально). Рассмотрим методику проверки гипотезы о нормальном законе распределения результатов наблюдений при 15<n<50. В этом случае используется составной критерий, включающий в себя критерий 1 и критерий 2. Гипотеза считается не противоречащей результатам наблюдений при уровне значимости Критерий 1. Вычисляют значение d
Затем задаются уровнем значимости
Критерий 2. Определяют значение m:
Затем задаются уровнем значимости
Гипотеза, удовлетворяет критерию 2, если
Таблица 4.1 Значения d1 и d2
Таблица 4.2 Значения z
Задача По данным, приведенным в табл.3.3. проверить гипотезу о согласованности эмпирического и теоретического распределения по составному критерию.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 1409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.59.187 (0.007 с.) |
 (4.1)
(4.1)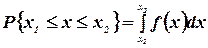 . (4.2)
. (4.2) , которое принимается за результат измерения, если подтверждается гипотеза о нормальном распределении результатов наблюдений и ряд наблюдений не содержит промахов.
, которое принимается за результат измерения, если подтверждается гипотеза о нормальном распределении результатов наблюдений и ряд наблюдений не содержит промахов. ; (4.3)
; (4.3) ; (4.4)
; (4.4) . (4.5)
. (4.5) . (4.6)
. (4.6) , если требования критерия 1 выполняются при уровне значимости
, если требования критерия 1 выполняются при уровне значимости  , а критерия 2 – при уровне значимости
, а критерия 2 – при уровне значимости  . Рекомендуются значения уровня значимости
. Рекомендуются значения уровня значимости  от 0,02 до 0,10.
от 0,02 до 0,10.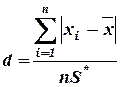 . (4.7)
. (4.7)
 , удовлетворяющих неравенству
, удовлетворяющих неравенству  .
. .
.


