
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи розрахунку відкосів, засновані на гіпотезі криволінійної поверхні здвиганняСодержание книги
Поиск на нашем сайте
Методи розрахунку відкосів, засновані на криволінійній повер-хні здвигання, можна поділити на дві групи. До першої відносяться методи, в яких форма поверхні здвигання визначається у ході вирі-шення задачі. У методах другої групи криволінійна форма поверхні приймаєть-ся заздалегідь, а сам метод зводиться до алгоритму побудови цієї поверхні. Однією з перших у цій області була робота К. Терцагі. Об’єм породи, розміщений між поверхнею оголення відкосу і поверхнею можливого ковзання, називають призмою можливого об-валення. Здвигання сили на поверхні можливого ковзання обумов-люються, в основному, вагою порід призми обвалення. Для оцінки стійкості відкосу в масиві відшукують найбільш слабку поверхню, де утримуючі сили Метод Ю.М. Соловйова заснований на прийнятті моделі гіпоте-тичного ґрунту, особливістю якої є припущення про те, що у верти-кальних площинах породного масиву відсутні нормальні напружен-ня а, отже, між вертикальними блоками, на які умовно розбита призма можливого обвалення, відсутні сили тертя. Задача зводиться до визначення екстремальної поверхні здвигання, тобто такої повер-хні, вздовж якої опір зрушенню буде найменшим. Розрахункова схема приведена на рис. 3. Розглядається умова рівноваги точки m, яка лежить на екстра-мальній поверхні здвигання:
де а – деяка дуже мала величина.
Рис. 3. Розрахункова схема для визначення положення екстремальної поверхні здвигання Визначимо величини, що входять у рівняння (8):
З врахуванням (9) рівняння рівноваги (8) набуде вигляду:
Визначимо кут нахилу поверхні здвигання таким чином, щоб величина а була мінімальною. Для цього продиференціюємо рівня-ння (10) один раз по змінній q і прирівняємо отриманий вираз до нуля:
Одержимо рівняння екстремальної поверхні здвигання:
Для побудови поверхні зрушення за цим методом, який часто називають методом відсоків, необхідно знати початкове значення Zі і від точки до точки визначати екстремальне положення поверхні здвигання.
К. Терцаги вперше був запропонований так званий графоаналі-тичний метод, суть якого полягає в припущенні, що поверхня зру-шення є кругло циліндричною. Розрахунок проводиться методом наближення, суть якого в пов-торенні розрахунків для декількох можливих поверхонь ковзання. Найбільш небезпечною (екстремальною) буде поверхня, для якої коефіцієнт стійкості буде мінімальним. Для забезпечення стійкого положення відкосу мінімальний кое-фіцієнт стійкості повинний бути не меншим 1,5. Якщо він вия-виться меншим, необхідно зробити відкіс більш пологим і повто-рити розрахунки. Сутність методу полягає в наступному. На розрізі відкосу, який викреслюється у визначеному масштабі, наноситься ряд можливих циліндричних поверхонь ковзання (рис. 4, а), кожна з який забезпе-чує визначений, поки невідомий, коефіцієнт запасу міцності kі. Довжина можливих поверхонь ковзання вздовж фронту робіт прий-мається рівною одиниці. Кожна з призм ковзання розбивається на вертикальні відсіки однакової ширини b (рис. 4, б). Взаємодія між відсіками відсутня.
Рис. 4. Схеми для розрахунку стійкості відкосів за К. Терцаги Вага кожного з відсіків Qi розкладається на складові:
Для визначення коефіцієнта стійкості kі відкосу розглядають співвідношення моментів сил, що діють відносно точки О:
де Му – момент сил, що утримують відкіс від сповзання; Мс – момент сил, що здвигають відкіс. Момент сил, що утримує відкіс, рівний:
де С – зчеплення, ρ – кут внутрішнього тертя, l – довжина дуги, R – радіус поверхні ковзання. Момент сил, який здвигає відкіс рівний:
Із врахуванням отриманих співвідношень отримаємо формулу для визначення коефіцієнта стійкості відкосу:
Графоаналітичний метод К.Терцаги дає позитивні результати для порівняно однорідних і необводнених порід.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.234.123 (0.011 с.) |

 знаходяться по відноше-нню до здвигаючих сил
знаходяться по відноше-нню до здвигаючих сил  у найбільш несприятливому відноше-нні. Форма поверхні можливого ковзання залежить від баготьох факторів – механічної міцності масиву, тріщинуватості, шаруватості і т.п.
у найбільш несприятливому відноше-нні. Форма поверхні можливого ковзання залежить від баготьох факторів – механічної міцності масиву, тріщинуватості, шаруватості і т.п. (8)
(8)
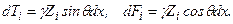 (9)
(9) (10)
(10)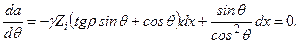 (11)
(11) (12)
(12)
 і
і 
 (13)
(13) (14)
(14) (15)
(15) (16)
(16)


