
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напружений стан гірських порідСодержание книги
Поиск на нашем сайте
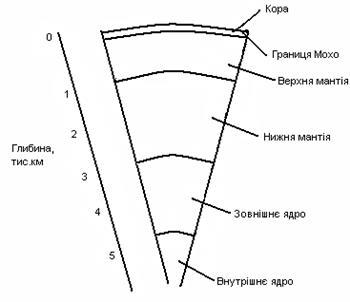
За сучасними уявленнями, одержаними для глибинних зон на підставі сейсмічних досліджень, в Землі виділяють кору, верхню і нижню мантію, зовнішнє і внутрішнє ядро (рис. 2).
Рис. 2. Загальна схема внутрішньої будови Землі Середня потужність зовнішньої твердої оболонки Землі (земної кори) 32 км, причому на континентах вона змінюється в межах 20…70 км, в океанах – 5…15 км. Глибше знаходиться верхня ман-тія, відділена від земної кори поверхнею розподілу Мохоровича (або, коротко, розділу Мохо) – сейсмічною межею, на якій швид-кість подовжніх пружних хвиль Vр стрибкоподібно зростає до значень більше 8 км/с, тоді як в земній корі вона складає звичайно 6…7 км/с (максимальне значення 7,4 км/с). Земна кора і верхня мантія утворюють так звану тектоносферу – область прояву в Землі тектонічних процесів. У межах земної кори виділяють за сейсмологічними характери-тиками три основні шари. Верхній – осадовий, характеризується швидкостями розповсюдження подовжніх пружних хвиль у межах 2,0…5,0 км/с. Його максимальна потужність звичайно не перевищує 10…15 км. Наступний шар має умовну назву гранітного, оскільки в ньому швидкість подовжніх хвиль Vр =5,5…6,0 км/с. Максимальна потужність гранітного шару 30…40 км. Нижній шар земної кори, названий базальтовим, характеризується значенням Vр =6,5...7,4 км/с. Його потужність 15…20 км. Гранітний і базальтовий шар розділені поверхнею Конрада – сейсмічною межею зміни швидкості пружних хвиль між цими двома шарами. Отже, основна концепція сучасної механіки гірських порід полягає в тому, що напружений стан в цілому і верхньої її частини, визначається дією в земній корі двох незалежних силових полів. Одне з них – гравітаційне поле. Інше – тектонічне поле, обумовлене нерівномірним розподілом у просторі швидкості тектонічних рухів і швидкості деформацій земної кори. Гравітаційне поле згідно закону всесвітнього тяжіння володіє такою особливістю, що воно не може бути відділене від мате-ріальних тіл, які його породили. Тектонічне силове поле є значно складнішим, бо тектонічні рухи зумовлюють появу горизонтальних сил, які в сейсмології і геотек-тоніці оцінюють за максимальним дотичним напруженням. Досить суттєву інформацію про характер напруженого стану масиву порід можуть дати дані про вивалювання, які відбуваються відразу після відбою порід, раптових обвалах, поштовхах, стрілянні порід, які відбуваються під час проведення гірничо прохідних робіт.
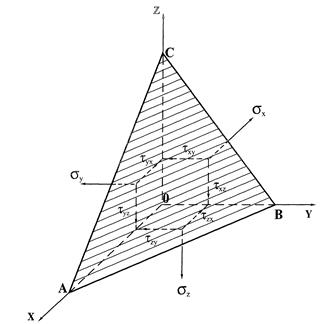
Величина, яка характеризує інтенсивність розподілу внутрішніх сил, називається напруженням. Навколо виробки утворюються поля напружень. Приймаючи до уваги гіпотезу про однорідність і безперервний розподіл речовини, виділимо в породному масиві, який знаходиться в рівновазі, довіль-ну точку. Напружений стан у точці може бути визначений заданням векторів напружень sх, sу, sz в трьох взаємно перпендикулярних площинах, що проходять через цю точку (рис. 3).
Рис. 3. Позначення компонентів напружень на косій довільно орієнтованій площині Пересікаючись, ці площадки утворюють деяку прямокутну систему координат в якій ми маємо три компоненти нормального Знаючи величини і напрямки нормальних і дотичних напружень в трьох взаємно перпендикулярних площинах, які приймаються за координатні площини, можна знайти напруження в любій площині, яка проходить через точку, що розглядається, якщо відомі напрямні косинуси l, m, n нормалі v до цієї площини відносно вибраних осей. Отже, повне напруження Рv можна розкласти на складові, які паралельні координатним осям Хv, Yv, Zv. Тоді з умов рівноваги піраміди АВС0 отримаємо наступні вирази:
Повне напруження Рv на нахиленій площині визначається на-ступним чином:
Види напруженого стану У загальному випадку напружено-деформований стан виділеного елементарного об'єму в колі даної точки характеризується наявні-стю дев'яти компонентів напружень і дев'яти компонентів дефор-мацій. Такий напружено-деформований стан, називається об'ємним. Вирішення об'ємних задач навіть тільки із застосуванням методів теорії пружності пов’язане із значними математичними трудноща-ми. Тому вирішення будь-якої геомеханічної задачі починають з аналізу особливостей напружено-деформованого стану для того, щоб спростити початкову розрахункову схему і привести її по можливості до так званої плоскої задачі, коли всього лише два компоненти напружень і два компоненти деформацій залежать від координат точок тіла.
Плоский напружений стан не є харак-терним для задач геомеханіки. Але спро-щення, подібні приведеним вище, мож-ливі і в іншому граничному випадку, коли розмір тіла у напрямку осі Z дуже великий. Це можуть бути, наприклад, підпірна стінка або довга горизон-тальна виробка, лава і т.п. (рис. 5, а), б)). Якщо розглядається напружено-деформований стан масиву навколо виробки на достат-ній віддалі від її торців, то всі перетини, перпендикулярні повздов-жній осі виробки Z, знаходитимуться в однакових умовах.
Рис. 5. Плоский деформований стан Компоненти переміщень U і h не залежать від координати Z і є функціями координат Х і У. Поздовжні переміщення T при цьому рівні нулю. Такий напружений стан називається плоскою деформа-цією. Співвідношення матиме вигляд:
Граничні умови рівноваги Рівняння рівноваги повинні задовольнятися в усіх точках дослі-джуваного тіла. При досягненні границі області компоненти напру-жень повинні бути такими, щоб вони знаходилися в рівновазі із зовнішніми силами, прикладеними до границі. Через це зовнішні сили можна розглядати, як продовження внутрішніх напружень. Розглянемо малу трикутну призму, гіпотенуза якої співпадає з границею тіла (рис. 6). Позначимо через
де 1, m – направляючі косинуси нормалі v до границі.
Рис.6.Для визначення граничних умов В окремому випадку розгляду рівноваги прямокутної пластинки координатні осі за звичай направляють паралельно граням плас-тинки і граничні умови (5) можна спростити. Нехай, наприклад, одна із сторін пластинки паралельна осі X, тоді нормаль v на цій частині границі буде паралельна осі Y; звідси 1 =0, m =1. Рівняння (5) у цьому випадку набудуть вигляду:
причому знак (+) береться в тому випадку, якщо нормаль проведена у бік позитивних значень Y; в протилежному випадку береться знак (–). З останніх формул видно, що компоненти напружень на границі рівні компонентам поверхневих зусиль, віднесених до одиниці пло-щі границі.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.235 (0.011 с.) |

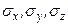 і шість дотичних напружень –
і шість дотичних напружень – 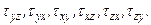
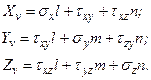 (2)
(2)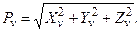 (3)
(3) Так, наприклад, якщо тонку пластину, що знаходиться в стані рівноваги під дією зовнішніх сил, навантажити рівномірно розпо-діленими по товщині зусиллями, прикладеними до її границі пара-лельно площині пластини, то компоненти напружень
Так, наприклад, якщо тонку пластину, що знаходиться в стані рівноваги під дією зовнішніх сил, навантажити рівномірно розпо-діленими по товщині зусиллями, прикладеними до її границі пара-лельно площині пластини, то компоненти напружень 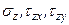 на обох поверхнях пластини будуть рівні нулю і можна припустити, що вони рівні нулю і всередині пластини (рис. 4).
на обох поверхнях пластини будуть рівні нулю і можна припустити, що вони рівні нулю і всередині пластини (рис. 4).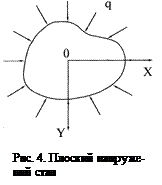 Такий напружений стан визначати-меться тільки компонентами напружень
Такий напружений стан визначати-меться тільки компонентами напружень 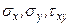 і називається плоским напру-женим станом. Доведено, що в тонких пластинах всі три невідомі компоненти напружень не залежать від координати Z, а є тільки функціями координат Х і У.
і називається плоским напру-женим станом. Доведено, що в тонких пластинах всі три невідомі компоненти напружень не залежать від координати Z, а є тільки функціями координат Х і У.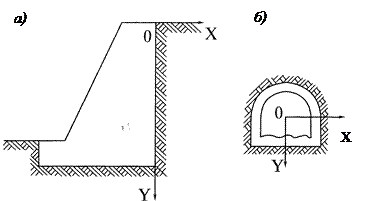
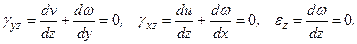 (4)
(4)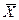 і
і 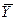 компоненти поверхневих сил Р, віднесених до одиниці поверхні в цій точці границі. Рівняння рівноваги матимуть вигляд:
компоненти поверхневих сил Р, віднесених до одиниці поверхні в цій точці границі. Рівняння рівноваги матимуть вигляд: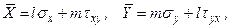 (5)
(5)
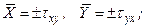 (6)
(6)


