
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорія руйнування гірських порід у складному напруженому станіСодержание книги
Поиск на нашем сайте
Передумова про малий вплив проміжного по величині напру-ження на руйнування гірських порід є єдиною в теорії Мора, яка в основному не вимагає перевірки, оскільки цілком ґрунтується на експериментальних даних. Однак, аналітичний критерій міцності отримується шляхом підбору відповідного емпіричного виразу і його застосування обмежується власне кажучи тією областю напру-жених станів, у якій виконані експерименти. Таким чином, експериментальний характер забезпечує досить точний опис граничного стану матеріалу, емпіричний же підбір умови міцності не дає можливості повною мірою скористатися цією перевагою. Тому цікавим є висновок аналітичного критерію теорії на основі аналізу процесу руйнування в локальній області твердого тіла, що може бути представлений наступним способом. Дотичні напруження, величина яких досить повно характеризується інтенсивністю напружень Ряд сучасних теорій міцності був отриманий на основі моделі руйнування твердих тіл із загальної функціональної залежності, яка об’єднує в одне співвідношення інтенсивності напружень і компо-ненти шарового тензора I:
де а, b, c – деякі параметри, визначені з випробувань при найпрос-тіших напружених станах:
Наступна гіпотеза Мора, припустимо, що міцність матеріалу практично залежить тільки від тих членів рівняння (6) і (7), які визначають різницю і суму найбільшого і найменшого компонентів напружень. Тоді з (5) при
Параметри b і с визначимо з (8) у результаті вимірювань гірських порід при найпростіших напружених станах: при одновісному стис-ненні отримаємо
при одновісному розтягуванні
Розв’язуючи рівняння (9) і (10) отримаємо:
Підставивши значення параметрів (11) у відношенні (8), отри-маємо наступну умову міцності:
або в загальному вигляді напруженого стану:
З рівняння (12) отримаємо:
де
Відмітимо, що при осесиметричному розподіленні напружень Для матеріалів, які однаково протидіють стисненню і розтягу, При
Позначимо відповідно максимальне дотичне напруження і величину, яка характеризує вид напруженого стану, як
Залежність (17) в системі координат « У системі координат «
Рис. 4. Поверхні граничних станів за формулою (3.17) Таким чином, отримана умова міцності відповідає вимогам пос-тулату Друккера і відповідає сучасним уявленням про природу руй-нування твердих тіл. Руйнування крихких матеріалів досить добре описується теорією Гриффітса. Муррель показав, що в системі координат «
Якщо в залежність (17) підставити, згідно Гриффітсу, y=1/8 і порівняти її з залежністю (18), то виявиться, що аналітичні вирази двох теорій міцності, отримані на основі різних фізичних представ-лень про природу руйнування, є практично ідентичними. Умова міцності (12) при На рис. 5 і рис. 6 показана теоретична крива залежності (12) у системі безрозмірних координат (
Рис. 5. Порівняння аналітичного критерію (12) з результатами іспитів гірських порід і бетону: о – вапняк,
Із виразу (12) може бути отримана формула для приведення склад-ного напруженого стану до простого одноосного. Вона має наступний вигляд:
де Використовуючи формулу (19) можна за допомогою коефіцієнта запасу міцності n оцінити ступінь небезпеки руйнування породного середовища для будь-якої точки однорідного породного масиву в околиці виробки, порівнюючи величину
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.149.244 (0.006 с.) |

 , розпушують матеріал шляхом здвига-ння, а під дією нормальних напружень, рівень яких визначається кульковим тензором I, відбувається розкриття тріщин.
, розпушують матеріал шляхом здвига-ння, а під дією нормальних напружень, рівень яких визначається кульковим тензором I, відбувається розкриття тріщин. (5)
(5) (6)
(6) (7)
(7) , отримаємо наступний вираз:
, отримаємо наступний вираз: (8)
(8)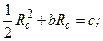 (9)
(9) (10)
(10) де
де  (11)
(11) (12)
(12) (13)
(13) (14)
(14) (15)
(15) Звідси слідує, що вираз (14) є умовою міцності Треска-Сен-Венана. В загальному ж випадку напруженого стану перша частина умови (14) залежить від значень компонентів напруження.
Звідси слідує, що вираз (14) є умовою міцності Треска-Сен-Венана. В загальному ж випадку напруженого стану перша частина умови (14) залежить від значень компонентів напруження. . У цьому випадку із виразу (14) отримаємо теорію Кулона.
. У цьому випадку із виразу (14) отримаємо теорію Кулона. із (12) отримаємо наступний частковий вираз теорії міцності:
із (12) отримаємо наступний частковий вираз теорії міцності: (16)
(16)
 і
і 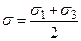 . Тоді вираз (12) з урахуванням прий-нятих позначень набуде вигляду:
. Тоді вираз (12) з урахуванням прий-нятих позначень набуде вигляду: (17)
(17) » являє рівняння параболи, що є опуклою і безперервною кривою.
» являє рівняння параболи, що є опуклою і безперервною кривою. » рівняння (12) має вигляд пара-боли, рівно нахиленої до осей і відкритої зі сторони стискаючих напружень, що відповідає вимозі симетричності умови виникнення граничного напруженого стану (рис.4). Із збільшенням величини y від 0 до 1 парабола витягається в сторону всебічного розтягання, що підтверджується дослідами Г.В. Ужика. І при
» рівняння (12) має вигляд пара-боли, рівно нахиленої до осей і відкритої зі сторони стискаючих напружень, що відповідає вимозі симетричності умови виникнення граничного напруженого стану (рис.4). Із збільшенням величини y від 0 до 1 парабола витягається в сторону всебічного розтягання, що підтверджується дослідами Г.В. Ужика. І при 
 (18)
(18)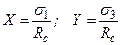 ) і результати випробувань гірських порід, одержані А.Н. Ставрогіним і X. Куком.
) і результати випробувань гірських порід, одержані А.Н. Ставрогіним і X. Куком.
 – аргіліт, ▲ – талькохлорит, -о- – мармур 1, + – діабаз, * – діорит, -☼- – алевроліт Д-19, піщаник Д-12, ● – бетон.
– аргіліт, ▲ – талькохлорит, -о- – мармур 1, + – діабаз, * – діорит, -☼- – алевроліт Д-19, піщаник Д-12, ● – бетон. Незважаючи на деяке наявне розкидання екс-периментальних точок, неминуче при випробу-ваннях структурно не-однорідних матеріалів, якими є гірські породи і бетони, з рисунків випливає, що запропо-нована умова міцності (12) досить добре опи-сує процес їхнього руй-нування при об'ємному стисканні і стисканні з розтягом.
Незважаючи на деяке наявне розкидання екс-периментальних точок, неминуче при випробу-ваннях структурно не-однорідних матеріалів, якими є гірські породи і бетони, з рисунків випливає, що запропо-нована умова міцності (12) досить добре опи-сує процес їхнього руй-нування при об'ємному стисканні і стисканні з розтягом. (19)
(19) – еквівалентне напруження, тобто напруження, подібне одно-вісному напруженому стану.
– еквівалентне напруження, тобто напруження, подібне одно-вісному напруженому стану. (20)
(20)


