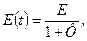Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про теорію спадкової повзучостіСодержание книги
Поиск на нашем сайте
Згідно сучасних уявлень, напруження, що виникають у реальних тілах, складаються з двох частин: перша складова залежить від деформації в даний момент часу t, друга – від деформацій, що існували в тілі протягом часу, що передував справжньому моменту часу – t. Час змінює структуру. Теорія, що дозволяє визначати деформації в середовищі з ураху-ванням історії її навантаження, називається теорією спадкової повзучості.
Теорія лінійної спадковості була запропонована Л. Больцманом з вико-ристанням математичного апарату ін-тегральних рівнянь В. Вольтера. Відповідно до цієї теорії, дефор-мації середовища під дією зовнішніх сил продовжуються і після їх прик-ладання (спадковість), при цьому де-формації в кожен момент часу прямо пропорційні діючим у різні моменти часу напруженням (лінійність) суму-ються, ростуть у часі (принцип суперпозиції). Проілюструємо вище викладене на наступному прикладі. Побу-дуємо криві повзучості g=f(t, s) при різних рівнях напруження (рис. 1, а). Потім в координатах «s - g» побудуємо графіки в моменти часу ti (і =1,2,3...) (рис. 1, б). Якщо ізохорні залежності, що вийшли при цьому, є прямими лініями (або близькими до них), то ми маємо справу з лінійним спадковим середовищем. Повзучість матеріалів в теорії лінійної спадковості описується інтегральним рівнянням Вольтера другого роду:
де s(t) і γ(t) – напруження і деформації в даний момент часу t, t – час, який передує моменту часу t; L(t) – деяка функція, яка враховує вплив часу на деформації і напруження в тілі. При
Диференціюючи обидві частини рівняння (2) по часу, отримаємо вираз:
з якого слідує, що L(t) являє собою функцію швидкості повзучості. Функцію ж L(t–t) називають ядром інтегрального рівняння Воль-тера (1). Розв’язуючи це відносно s(t), отримаємо,
При
Диференціюючи обидві частини (4) по t, отримаємо вираз для K(t):
Функції K(t) і L(t) взаємопов’язані і це дозволяє за однією з них знайти іншу. Функція K(t) називається резольвентою інтегрального рівняння Вольтера (2). Рівняння повзучості (2) можна записати у вигляді:
де Ю.Н. Работнов показав, що задачу лінійної спадковості можна формально розглядати, як задачу теорії пружності, в якій замість пружних постійних Е і m необхідно використовувати їх тимчасові аналоги (інтегральні оператори)
де d і a – реологічні характеристики, отримані експериментально. Інтегральне рівняння повзучості з ядром Абеля має наступний розв’язок:
Складність рішення задач методами теорії спадкової повзучості полягає в розшифровці тимчасових операторів. Часто при постійності граничних умов для вирішення задач геомеханіки використовують метод змінних модулів, який полягає у тому, що замість інтегральних операторів З виразу (5) слідує, що функція часу модуля деформації має вигляд
де Ф – функція повзучості, яка рівна:
Функція часу для коефіцієнта Пуассона визначається за формулою:
Слід відмітити, що використання теорії спадкової повзучості виправдане тільки в тому випадку, коли діюче напруження не перевищує тривалої міцності масиву.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.117.52 (0.009 с.) |

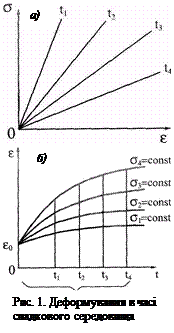 Теорія спадкової зміни внутрішніх чинників з урахуванням «пам'яті» ма-теріалу про всі тимчасові структурні зміни, що виникають у процесі наван-таження, і допускаюча лінійну залеж-ність між напруженнями і деформація-ми у будь-який момент часу, одержала назву теорії лінійної спадкової повзу-чості.
Теорія спадкової зміни внутрішніх чинників з урахуванням «пам'яті» ма-теріалу про всі тимчасові структурні зміни, що виникають у процесі наван-таження, і допускаюча лінійну залеж-ність між напруженнями і деформація-ми у будь-який момент часу, одержала назву теорії лінійної спадкової повзу-чості. (1)
(1) із співвідношення (1) отримаємо рівняння повзучості деформацій:
із співвідношення (1) отримаємо рівняння повзучості деформацій: (2)
(2)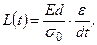
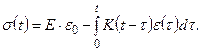 (3)
(3)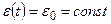 з (3) отримаємо рівняння релаксації на-пружень:
з (3) отримаємо рівняння релаксації на-пружень: (4)
(4)

 – тимчасовий оператор, який визначається у результаті оброб-ки експериментальних даних.
– тимчасовий оператор, який визначається у результаті оброб-ки експериментальних даних. . Ж.С. Ержанов встановив, що деформація ряду гірських порід до певного рівня навантаження відповідає рівнянню (2) з ядром повзучості у вигляді степеневої функції (ядро типу Абеля):
. Ж.С. Ержанов встановив, що деформація ряду гірських порід до певного рівня навантаження відповідає рівнянню (2) з ядром повзучості у вигляді степеневої функції (ядро типу Абеля):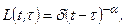
 (5)
(5)