
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретико – множний зміст кількісного числа і нуля.Содержание книги
Поиск на нашем сайте
Кількісне натуральне число являється загальною властивістю класу скінчених рівно потужних множин. Кожному класу відповідає єдине натуральне число, кожному натуральному числу – єдиний клас рівно потужних множин. Число нуль також має теоретико - множинний зміст – воно ставиться в відповідність пустій множині. Коли учні вивчають число «один», то на сторінці підручника приводяться зображення одного предмета, число «три» - сукупність трьох предметів. Так відбувається при вивченні всих чисел першого десятку, але число елементів множини визначається перерахуванням. Таким чином, кількісні і порядкові числа виступають в початковому навчанні в єдності. 4. Додавання. Закони додавання. Розглянемо задачу, яку розв‘язують першокласники: «Петрик знайшов 4 гриба, а Катя – 3. скільки всього грибів знайшли діти?». Для пояснення розв‘язання цієї задачі уявимо умову наглядно. Щоб дати відповідь на питання, потрібно до грибів Петрика додати (приєднати) гриби Каті, тобто об‘єднати дві множини грибів, і перерахувати кількість елементів нової множини. Сумою цнч а і в називають число елементів в об‘єднанні неперетинаючихся множина і В. сума цнч завжди існує і єдина. Дія, при якій знаходять сума називається додаваня, а числа, які додають – доданками. Сума трьох доданків визначається наступним чином: Закони додавання: 1. Комутативний (переставний) 2. Асоціативний (сполучний) Наприклад, раціонально обчислити значення виразу 109+ 36 + 191 +64+27=ком. закон = 109+191 + 36+64 +27=ас. закон =(109+191)+(36+64)+27=300+100+27=ас. закон =(300+100)+27=400+27=427.
Лекція 9,10. Теоретико – множний підхід до побудови цілих невід‘ємних чисел. Мета: розглянути теоретико – множний підхід до дій над цілими невід‘ємними числами, законами, дій над числами. Пояснити застосування законів при розв‘язанні практичних задач. Закріпити вміння і навички студентів використовувати раціональний спосіб розв‘язання. Розвивати усний рахунок і пам‘ять студентів. План: 1. Порівняння чисел. 2. Віднімання. 3. Множення, закони множення. 4. Ділення. 5. Ділення з залишком.
1. Порівняння. Нагадаємо, що два числа Якщо число Число 2. Віднімання. Задача: «Коло школи росли 8 дерев – тополь і беріз. Беріз 3, а скільки тополь?». Різницею чисел
Різницею чисел Дія за допомогою якої знаходять різницю називається відніманням, а компоненти: зменшуване, від‘ємник, різниця. Різниця чисел В початковій школі спочатку віднімання чисел розглядається на основі практичних вправ, пов’язаних з виділенням підмножини заданої множини і утворенням нової множини – доповнення виді ленної підмножини. Відношення «більше на», «менше на». Який зміст цих відношень? Припустимо, що числа Правила віднімання числа з суми і суми із числа: · · Щоб відняти від числа суму чисел, достатньо відняти від цього числа послідовно доданки:
3. Множення. Задача: «На кожне дитяче пальто потрібно пришити по 4 ґудзика. Скільки ґудзиків знадобиться для 6 пальт?». Добутком чисел 1) 2) 3) Дія за допомогою якої знаходять добуток чисел називається множенням, а компоненти: перший множник, другий множник, добуток. Добуток чисел Добуток існує і тільки один. Закони множення: Комутативний (переставний)- Асоціативний (сполучний)- Дистрибутивний (розподільний) по відношенню до додавання Наприклад, користуючись законами множення обчислити значення виразу:
4. Ділення. Припустимо Дія за допомогою якої знаходять частку називають ділення, а компоненти: ділене, дільник, частка. Правильність ділення перевіряється множенням. Ч асткою чисел Щоб частка існувала необхідно, щоб Щоб знати, у скільки разів одне число більше за інше, необхідно більше число поділити на менше. Наприклад, «У Каті 6 зошитів, а у Дмитра в два рази менше. Скільки зошитів у Дмитра?» і «Купили 3 парти і 12 стільців. У скільки раз менше купили парт, ніж стільців?». Правило ділення суми на число: якщо числа Правило ділення числа на добуток: якщо число Правило добутку числа на частку: щоб помножити число на частку чисел, достатньо помножити це число на ділене і отриманий добуток поділити на дільник: 5. Ділення з залишком. Число 37 на 8 не ділиться, але існують такі числа 4 і 5, що
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.239.0 (0.006 с.) |

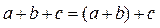 .
. .
.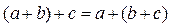 .
. і
і 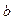 з теоретико – множної точки зору представляють собою кількість елементів множин. Два числа
з теоретико – множної точки зору представляють собою кількість елементів множин. Два числа 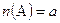 і
і  .
. і навпаки. Якщо множина А рівносильна власній підмножині В, то кажуть що
і навпаки. Якщо множина А рівносильна власній підмножині В, то кажуть що 
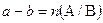 , де
, де  .
.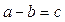
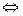
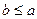 . Вірність даної операції перевіряється додаванням. Якщо різниця існує, то вона єдина.
. Вірність даної операції перевіряється додаванням. Якщо різниця існує, то вона єдина. Щоб відняти число від суми, достатньо відняти його з одного з доданків і до отриманого результату додати інший доданок: а) якщо
Щоб відняти число від суми, достатньо відняти його з одного з доданків і до отриманого результату додати інший доданок: а) якщо 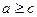 , то
, то 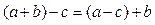 , б) якщо
, б) якщо 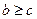 , то
, то 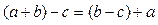 .
.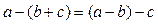 .
.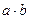 , яке задовольняє умовам:
, яке задовольняє умовам: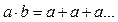 (
(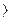 1.
1.
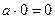 .
.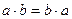 ,
,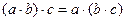 ,
,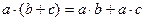 і по відношенню до віднімання
і по відношенню до віднімання  .
. .
.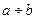 , добуток якого з числом
, добуток якого з числом 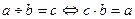 .
. .
.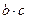 , достатньо поділити число
, достатньо поділити число 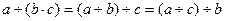 .
.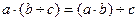 .
.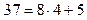 . Поділити число з залишком на інше число – це значить знайти такі цілі невід‘ємні числа
. Поділити число з залишком на інше число – це значить знайти такі цілі невід‘ємні числа  і
і  , що
, що  . Залишок обов‘язково має бути меншим дільника.
. Залишок обов‘язково має бути меншим дільника.


