
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 3. Математичні доведення.Содержание книги
Поиск на нашем сайте
Мета: Основні питання: 1. Відношення рівнозначності між твердженнями. 2. Необхідні і достатні умови. 3. Структура і види теорем. 4. Дедуктивні міркування. 5. Найпростіші схеми дедуктивних міркувань. 6. Неповна індукція. I. Відношення рівнозначності між твердженнями. Будь-яке міркування не обходиться без слів «випливає», «значить». Кажуть, що з твердження А випливає твердження В, якщо всякий раз, коли істинний вислів А, істинним є вислів В. наприклад, твердження «із того, що число а кратно 4, випливає, що воно кратно 2» можна сформулювати ще і так: всяке число, яке ділиться на 4, ділиться на 2, або якщо число ділиться на 4, то воно ділиться і на 2, число а ділиться на 4, значить воно ділиться на 2. Якщо із твердження А випливає твердження В, а із твердження В випливає твердження А, то кажуть, твердження А і В рівнозначні. Згідно цього означення твердження «трикутник «рівнобедрений» і «кути при основі трикутника рівні» є рівнозначними.
II. Необхідні і достатні умови. Якщо з твердження А випливає твердження В, то говорять, що В – необхідна умова для А, а А – достатня для В. іншими словами, вислів В називається необхідною умовою для А, якщо воно логічно випливає з А. вислів А називається достатньою умовою для В, якщо В з нього випливає. Якщо твердження А і В рівнозначні, то говорять, А – необхідна і достатня умова для В, і навпаки. Наприклад, в геометрії доведено, що з твердження «кути вертикальні» випливає твердження «кути рівні». тому згідно даному означенню можна сказати, що рівність кутів – необхідна умова для того, щоб кути були вертикальні, а вертикальність кутів є достатньою умовою для їх рівності. У зв‘язку з цим твердження «якщо кути вертикальні, то вони рівні» можна сформулювати інакше: для того, щоб кути були вертикальні, необхідно, щоб вони були рівні; для того, щоб кути були рівні, достатньо, щоб вони були вертикальні. III. Структура і види теорем. Раніше було відокремлено, що суттєві властивості об‘єкта утворюють зміст поняття про цей об‘єкт. Частина цих властивостей включається в означення поняття. Щоб мати більш повне уявлення про об‘єкт, вивчають і інші його властивості. Властивості основних (первісних) понять розкривається в аксіомах – твердженнях, які приймаються без доведення. Наприклад, властивості основних понять геометрії: точка, пряма, площини включені в аксіоми. Взагалі система аксіом будь-якої теорії, розкриваючи властивості основних понять, дає, по суті, їх означення, які називаються аксіоматичними. Властивості, які доводяться, найчастіше називають теоремами, іноді слідствами, признаками. В алгебрі – формулами, тотожностями, правилами. Тому, теорема – це висловлення про те, що з властивості А випливає властивість В. істинність цього вислову встановлюється шляхом доведення. В якому б виді не була сформульована теорема, в ній завжди виділяється умова А(що задано) і висновок В (що треба довести). Теореми IV. Дедуктивні міркування. Довести теорему V. Найпростіші схеми дедуктивних міркувань. Вважають, що в основі кожного дедуктивного міркування лежить певне правило висновку. 1) Правило висновку ( VI. Неповна індукція. Відомо, що 15 ділиться на 5, 25 ділиться на 5, 35 і 95 діляться на 5. враховуючи це, робимо висновок, що будь-яке число, запис якого закінчується цифрою 5, ділиться на 5. В розглянутому міркуванні на основі ряду часткових випадків робимо висновок загальний. Такі міркування називають неповною індукцією. Неповна індукція представляє собою таке міркування, при якому на основі того, що деякі об‘єкти сукупності мають певні властивості, робиться висновок про те, що ці властивості притаманні всім об‘єктам цієї сукупності. Висновки, отримані при неповній індукції, можуть бути як істинними, так і хибними. Так висновок про те, що кожне число, запис якого закінчується цифрою 5, ділиться на 5, істинний. А твердження «при будь-якому натуральному числі
Лекція5. Поняття множини. Мета: Основні питання: 1. Поняття множини і елемента множини. 2. Способи завдання множин. 3. Відношення між множинами. 4. Множина і поняття. I. Поняття множини і елемента множини. В математиці часто приходиться розглядати певні групи об‘єктів як єдине ціле: числа від 1 до 10, натуральні числа, трикутники. Всі ці різноманітні сукупності називають множинами. Поняття множини являється одним з основних понять математики і тому не має означення через інші поняття. Його можна пояснити на прикладах: множина учнів класу, множина букв алфавіту, натуральні числа. В математиці розглядають множину, яка містить один об‘єкт, або не містить жодного елемента, яка називається пустою. Об‘єкти, з яких складається множина, називають його елементами. Часто приходиться з‘ясовувати належність елемента до розглянутої множини. Множини бувають скінчені і нескінчені. Скінченою множиною називають таку, елементи якої можна перерахувати. Нескінченими являються і множини чисел. II. Способи завдання множин. Вважають, що множина визначається своїми елементами, тобто множина задана, якщо про будь-який об‘єкт можна сказати, належить він цій множині чи не належить. Множину можна задати, перерахувавши всі його елементи. Наприклад, III. Відношення між множинами. Задані дві множини: V. Множина і поняття. Як відомо, будь-яке поняття має об‘єм. З теоретик-множної позиції об‘єм поняття – це множина об‘єктів, які можна назвати одним словом, яке позначає поняття. Наприклад, об‘єм поняття «трикутник» - множина трикутників, об‘єм поняття «прямий кут» - множина прямих кутів. Підхід до об‘єму поняття як множині дає можливість наглядно уявити відношення між поняттями. Існують поняття, які не знаходяться в відношенні роду і виду. Наприклад, поняття «квадрат» і «трикутник» - їх об‘єми не знаходяться в відношенні включення.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.192.64 (0.011 с.) |

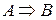 В – необхідна умова для А
А – достатня умова для В
В – необхідна умова для А
А – достатня умова для В
 називаються оберненими одна до іншої, а теореми
називаються оберненими одна до іншої, а теореми 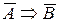 називаються протилежними. Наприклад, для теореми «якщо кути вертикальні, то вони рівні» оберненою є «якщо кути рівні, то вони вертикальні», що являється хибність. Протилежною до заданої є «якщо кути не являються вертикальними, то вони не рівні» також є хибність. А ось обернена до протилежної «якщо кути не рівні, то вони не вертикальні» являється істиною. Встановлено, теореми
називаються протилежними. Наприклад, для теореми «якщо кути вертикальні, то вони рівні» оберненою є «якщо кути рівні, то вони вертикальні», що являється хибність. Протилежною до заданої є «якщо кути не являються вертикальними, то вони не рівні» також є хибність. А ось обернена до протилежної «якщо кути не рівні, то вони не вертикальні» являється істиною. Встановлено, теореми  , тому що 7 при рахунку називають раніше, ніж 8». На які ж факти він опирався, стверджуючи це. По-перше, якщо число а при рахунку називають раніше числа в, то
, тому що 7 при рахунку називають раніше, ніж 8». На які ж факти він опирався, стверджуючи це. По-перше, якщо число а при рахунку називають раніше числа в, то 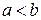 для будь-яких натуральних чисел. І по-друге, 7 при рахунку називають раніше, ніж 8. перше твердження носить загальний характер, так як містить квантор спільності, його називають загальною посилкою. Друге твердження стосується конкретних чисел 7 і 8, відображає частинний випадок, його називають частковою посилкою. З двох посилок і випливає новий факт
для будь-яких натуральних чисел. І по-друге, 7 при рахунку називають раніше, ніж 8. перше твердження носить загальний характер, так як містить квантор спільності, його називають загальною посилкою. Друге твердження стосується конкретних чисел 7 і 8, відображає частинний випадок, його називають частковою посилкою. З двох посилок і випливає новий факт 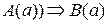 , де
, де 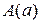 - часткова посилка і
- часткова посилка і  - висновок. 2) Правило заперечення
- висновок. 2) Правило заперечення  . 3) Правило силогізму
. 3) Правило силогізму 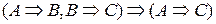 . Застосування цих правил гарантує, що міркування буде дедуктивним, тобто дозволяє з істинних посилок виводити істинні висновки. Наприклад, 1) Всі числа, запис яких закінчується нулем, діляться на 5; число не ділиться на 5, значить, його запис не закінчується 0. 2) Якщо натуральне число кратне 8, то воно кратне 4; якщо натуральне число кратне 4, то воно кратне 2; значить, якщо число кратне 8, то воно кратне 2. 3) Якщо запис числа закінчується нулем, то воно ділиться на 5; число не закінчується нулем, значить, воно не ділиться на 5.
. Застосування цих правил гарантує, що міркування буде дедуктивним, тобто дозволяє з істинних посилок виводити істинні висновки. Наприклад, 1) Всі числа, запис яких закінчується нулем, діляться на 5; число не ділиться на 5, значить, його запис не закінчується 0. 2) Якщо натуральне число кратне 8, то воно кратне 4; якщо натуральне число кратне 4, то воно кратне 2; значить, якщо число кратне 8, то воно кратне 2. 3) Якщо запис числа закінчується нулем, то воно ділиться на 5; число не закінчується нулем, значить, воно не ділиться на 5. 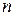 значення виразу
значення виразу 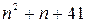 є просте число» хибне. Дійсно, якщо
є просте число» хибне. Дійсно, якщо 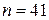 , то отримаємо значення
, то отримаємо значення 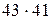 , тобто даний вираз є складовим числом. До висновків, отриманих за допомогою неповної індукції, треба відноситись критично. Ці висновки носять характер гіпотези, догадки, яку слідує або довести (дедуктивним методом), або спростити. Таким чином, в процесі пізнань дедуктивні і індуктивні міркування виявляються взаємозв‘язаними. При тому що індуктивні міркування не завжди приводять до правильних висновків, роль їх в вивченні математики і інших науках дуже велика. В ході індуктивних міркувань формується вміння бачити загальне в конкретних, часткових випадках, висловлювати догадки.
, тобто даний вираз є складовим числом. До висновків, отриманих за допомогою неповної індукції, треба відноситись критично. Ці висновки носять характер гіпотези, догадки, яку слідує або довести (дедуктивним методом), або спростити. Таким чином, в процесі пізнань дедуктивні і індуктивні міркування виявляються взаємозв‘язаними. При тому що індуктивні міркування не завжди приводять до правильних висновків, роль їх в вивченні математики і інших науках дуже велика. В ході індуктивних міркувань формується вміння бачити загальне в конкретних, часткових випадках, висловлювати догадки. 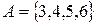 . Якщо множина нескінчена, то її елементи перерахувати не можна. В таких випадках вказують характеристичну властивість його елементів. Характеристична властивість – це така властивість, якою володіє кожний елемент, який належить множині, і не володіє жоден з елементів, який йому не належить. Для того щоб задати деяку множину, достатньо або перерахувати всі його елементи, або вказати характеристичну властивість його елементів. Наприклад, множина А натуральних чисел, менших 7, задана вказанням характеристичної властивості його елементів, можна задати і так:
. Якщо множина нескінчена, то її елементи перерахувати не можна. В таких випадках вказують характеристичну властивість його елементів. Характеристична властивість – це така властивість, якою володіє кожний елемент, який належить множині, і не володіє жоден з елементів, який йому не належить. Для того щоб задати деяку множину, достатньо або перерахувати всі його елементи, або вказати характеристичну властивість його елементів. Наприклад, множина А натуральних чисел, менших 7, задана вказанням характеристичної властивості його елементів, можна задати і так: 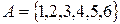 , тобто перерахував його елементи.
, тобто перерахував його елементи.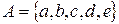 і
і  . Видно, що елементи
. Видно, що елементи 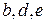 належать одночасно множині А і В. кажуть, що ці елементи – спільні для множин А і В, а самі множини перетинаються. Якщо множини не мають спільних елементів, то говорять, що вони не перетинаються. Множини
належать одночасно множині А і В. кажуть, що ці елементи – спільні для множин А і В, а самі множини перетинаються. Якщо множини не мають спільних елементів, то говорять, що вони не перетинаються. Множини  перетинаються, причому, кожний елемент множини В являється елементом множини А. в цьому випадку говорять, що множина В включена в А або що множина В являється підмножиною множини А. Множина В називається підмножиною множини А, якщо кожний елемент множини В належить множині А, і записують
перетинаються, причому, кожний елемент множини В являється елементом множини А. в цьому випадку говорять, що множина В включена в А або що множина В являється підмножиною множини А. Множина В називається підмножиною множини А, якщо кожний елемент множини В належить множині А, і записують 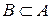 . Серед всіх підмножин заданої множини повинні бути обов‘язково пуста множина і сама множина. Якщо множини перетинаються, причому кожний елемент множини А являється елементом множини В, і навпаки, кожний елемент множини В являється елементом множини А, то говорять, що множини А і В є рівними. Тобто множини А і В називаються рівними, якщо
. Серед всіх підмножин заданої множини повинні бути обов‘язково пуста множина і сама множина. Якщо множини перетинаються, причому кожний елемент множини А являється елементом множини В, і навпаки, кожний елемент множини В являється елементом множини А, то говорять, що множини А і В є рівними. Тобто множини А і В називаються рівними, якщо 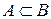 , записують
, записують  . З означення випливає, що рівні множини складаються з однакових елементів і що порядок запису елементів множини не являється суттєвим. Наглядно відношення між множинами зображають за допомогою особливих малюнків, які називають кругами Ейлера. Поняття множини і підмножини в початковій математиці в явній формі не вивчається, але задач, пов‘язаних з виділенням деякої сукупності, учні розв‘язують багато. Наприклад, «серед даних чотирикутників вказати прямокутники», «назвати серед даних чисел парні».
. З означення випливає, що рівні множини складаються з однакових елементів і що порядок запису елементів множини не являється суттєвим. Наглядно відношення між множинами зображають за допомогою особливих малюнків, які називають кругами Ейлера. Поняття множини і підмножини в початковій математиці в явній формі не вивчається, але задач, пов‘язаних з виділенням деякої сукупності, учні розв‘язують багато. Наприклад, «серед даних чотирикутників вказати прямокутники», «назвати серед даних чисел парні».


