
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 13, 14. Раціональні числа.
План: 1. Поняття дробу. 2. Поняття додатного раціонального числа. 3. Дії над раціональними числами. 4. Нескінчені періодичні десяткові дроби.
1. Поняття дробу. Зв'язок між множинами чисел можна уявити наглядно за допомогою кругів Ейлера. Нехай заданий відрізок Признак рівності дробів: для того, щоб дроби Властивість: якщо чисельник і знаменник дробу помножити на одне число, то отримаємо дріб, рівний даному. На цій властивості основане скорочення дробу і зведення дробів до спільного знаменника. Скорочення дробу - це заміна даного дробу іншим, що дорівнює даному, але з меншим чисельником і знаменником. Дріб Зведення дробів до спільного знаменника – це заміна дробів рівними їм, які мають спільний знаменник.
2. Поняття додатного раціонального числа. Додатне раціональне число – це множина рівних дробів, а кожний дріб, що належить цій множині, є запис цього числа. Наприклад, Для будь-якого додатного раціонального числа існує єдиний дріб, що не скорочується і являється записом цього числа. Множина додатних раціональних чисел позначається
3. Дії над додатними раціональними числами. 1) Сумою дробів Сума дробів з різними знаменниками є сумою дробів, зведених до спільного знаменника. Наприклад, Додавання раціональних чисел є комутативним Існують дроби правильні і неправильні. Дріб
2) Різницею додатних раціональних чисел називається таке число с, що 3) Добутком додатних раціональних чисел є число, яке знаходять за правилом: Добуток підкоряється комутативному закону 4) Часткою двох додатних раціональних чисел називається число В множині натуральних чисел є найменше число 1 і N – дискретна множина. В множині раціональних чисел 4. Нескінчені періодичні десяткові дроби. Візьмемо дріб Теорема. Якщо звичайний дріб З теореми випливає: будь-яке додатне раціональне число можна представити або скінченим десятковим дробом, або нескінченим періодичним дробом. Чисто періодичний нескінчений дріб дорівнює такому звичайному дробу, чисельник якого дорівнює періоду, а знаменник складається з стількох 9,скільки цифр в періоді дробу. Наприклад,
Лекція 15,16. Дійсні числа. План: 1. Поняття ірраціонального додатного числа. 2. Дійсні числа, дії над ними. 3. Від‘ємні числа.
1. Поняття ірраціонального додатного числа. Дії над раціональними числами зручно виконувати, коли вони записані десятковими дробами. Тому краще і результати вимірів величин представляти в виді десяткових дробів. Якщо уявити процес десяткового виміру довжини відрізку в ідеалі(як це роблять в математиці), то можливі два варіанта: 1) на якомусь кроці процес виміру відрізку скінчиться. Тоді довжина відрізку Множину додатних ірраціональних чисел позначають
2. Дії над дійсними числами. Множина додатних дійсних чисел Дії над додатними раціональними числами зводяться, в принципі, до дій над натуральними числами. Дії над нескінченими десятковими дробами можна звести до дій над раціональними, але необхідно ввести поняття приблизного значення дійсного числа за нестачею і залишком. Число Сумою дійсних чисел Наприклад, знайти суму двох чисел Добутком дійсних чисел Наприклад, обчислити добуток чисел Закони додавання і добутку дійсних чисел: 2) комутативний 3) асоціативний 4) дистрибутивний
3. Від’ємні числа. На координатній вісі усі точки, що стоять праворуч нуля являються додатними, а числа, що стоять ліворуч нуля називаються від’ємними. Числа, наприклад, 1 і -1 називають протилежними. Число нуль не являється ні додатним ні від’ємним. Усі точки координатної вісі відповідні дійсним числам. Множина дійсних чисел і координатна вісь знаходяться у взаємно однозначній відповідності: кожному дійсному числу відповідає єдина точка координатної прямої і навпаки. Відстань від нуля до точки, координата якої є число
Дії над числами: 1. Порівняння дійсних чисел: число 2. Сумою двох дійсних чисел 1). Сума додатних чисел є число додатне; наприклад, 123+56=179 2). Сума від’ємних чисел є число від’ємне: додаємо модулі доданків і в переді ставимо знак мінус; наприклад, -12+(-45)=-57. 3). Сума чисел з різними знаками - це число, яке має знак такий, як і доданок з більшим модулем, а модуль суми – це різниця між доданками з більшим і меншим модулем, наприклад, 96+(-54)=42, -56+48=-8. 3. Добутком чисел 1). Добуток додатних чисел є число додатне, наприклад, 2). Добуток від’ємних чисел є число додатне; наприклад, 3). Добуток чисел з різними знаками є число від’ємне, наприклад, 4. Віднімання і ділення – це дії, обернені додаванню і множенню.
II курс
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.28.48 (0.019 с.) |
 і одиничний відрізок
і одиничний відрізок 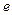 , причому відрізок
, причому відрізок  відрізків
відрізків  . Якщо відрізок
. Якщо відрізок  відрізків
відрізків  . Символ
. Символ  називають дробом, де
називають дробом, де  .
. були рівні, необхідно і достатньо, щоб
були рівні, необхідно і достатньо, щоб  .
.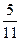 - дріб, що не скорочується. Результатом скорочення має бути дріб, що не скорочується.
- дріб, що не скорочується. Результатом скорочення має бути дріб, що не скорочується. .
. , в яку входить вся множина натуральних чисел
, в яку входить вся множина натуральних чисел  . Числа, які доповнюють множину
. Числа, які доповнюють множину  .
. .
. і асоціативним
і асоціативним  .
. .
. - це правило виділення цілої частини з неправильного дробу, результатом є мішане число. Будь-яке мішане число можна записати в виді неправильного дробу. Наприклад,
- це правило виділення цілої частини з неправильного дробу, результатом є мішане число. Будь-яке мішане число можна записати в виді неправильного дробу. Наприклад, 
 , або
, або  . Наприклад,
. Наприклад, 
 (для того щоб помножити два дроби потрібно добуток чисельників цих дробів записати в знаменник нового дробу, а добуток знаменників цих дробів записати в знаменник нового дробу). Наприклад,
(для того щоб помножити два дроби потрібно добуток чисельників цих дробів записати в знаменник нового дробу, а добуток знаменників цих дробів записати в знаменник нового дробу). Наприклад,  .
. і асоціативному
і асоціативному  .
. (щоб поділити дріб на дріб, потрібно перший дріб помножити на обернений до другого дробу). Наприклад,
(щоб поділити дріб на дріб, потрібно перший дріб помножити на обернений до другого дробу). Наприклад, 
 . Для того, щоб звичайний дріб записати як десятковий
. Для того, щоб звичайний дріб записати як десятковий  , його не можна записати десятковим дробом.
, його не можна записати десятковим дробом.  , але в цьому числі є періоди, такий дріб називається періодичним, пишуть
, але в цьому числі є періоди, такий дріб називається періодичним, пишуть  .
.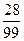 . Мішано періодичний дріб з нулем в цілій частині дорівнює такому звичайному дробу, чисельник якого дорівнює різниці між числом, що записане цифрами(стоять до початку другого періоду) і числом, що записане цифрами (стоять до початку першого періоду), а знаменник складається з такого числа 9, скільки цифр в періоді, і такого числа нулів, скільки цифр стоїть до початку першого періоду. Наприклад,
. Мішано періодичний дріб з нулем в цілій частині дорівнює такому звичайному дробу, чисельник якого дорівнює різниці між числом, що записане цифрами(стоять до початку другого періоду) і числом, що записане цифрами (стоять до початку першого періоду), а знаменник складається з такого числа 9, скільки цифр в періоді, і такого числа нулів, скільки цифр стоїть до початку першого періоду. Наприклад,  . Існують чисто періодичні дроби – в яких період починається одразу після коми, і мішано періодичні дроби – в яких між комою і періодом є інші десяткові знаки. Наприклад, 0,(857142) і 3,27(346).
. Існують чисто періодичні дроби – в яких період починається одразу після коми, і мішано періодичні дроби – в яких між комою і періодом є інші десяткові знаки. Наприклад, 0,(857142) і 3,27(346). буде виражена скінченим десятковим дробом виду
буде виражена скінченим десятковим дробом виду  . 2) описаний процес виміру довжини відрізку нескінчений. Тоді його представляють символом
. 2) описаний процес виміру довжини відрізку нескінчений. Тоді його представляють символом 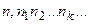 , який називають нескінченим періодичним дробом. Існують відрізки, довжина яких не являються періодичним десятковим дробом, тобто раціональним числом, при вибраній одиниці виміру. Такі нескінчені неперіодичні десяткові дроби називають додатними ірраціональними числами. Ірраціональні числа можна отримати і при знаходженні радикалів із деяких раціональних чисел, наприклад
, який називають нескінченим періодичним дробом. Існують відрізки, довжина яких не являються періодичним десятковим дробом, тобто раціональним числом, при вибраній одиниці виміру. Такі нескінчені неперіодичні десяткові дроби називають додатними ірраціональними числами. Ірраціональні числа можна отримати і при знаходженні радикалів із деяких раціональних чисел, наприклад  , а також ірраціональними є числа
, а також ірраціональними є числа 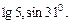 числа
числа 
 .
. - це об‘єднання множини додатних раціональних чисел і множини додатних ірраціональних чисел. Тому будь-яке дійсне число можна представити в виді нескінченого десяткового дробу – періодичного, якщо воно раціональне, або неперіодичного, якщо воно ірраціональне.
- це об‘єднання множини додатних раціональних чисел і множини додатних ірраціональних чисел. Тому будь-яке дійсне число можна представити в виді нескінченого десяткового дробу – періодичного, якщо воно раціональне, або неперіодичного, якщо воно ірраціональне. має приблизним значенням за нестачею з точністю до
має приблизним значенням за нестачею з точністю до  таке число
таке число  (тобто це число отримаємо, якщо залишимо цілу частину числа
(тобто це число отримаємо, якщо залишимо цілу частину числа  називають число
називають число  (тобто це число отримаємо, якщо в запису
(тобто це число отримаємо, якщо в запису  називається число
називається число  , яке задовольняє нерівності
, яке задовольняє нерівності  .
. з точністю до 0,001. Розглянемо їх приблизні значення
з точністю до 0,001. Розглянемо їх приблизні значення  , отже
, отже  і з точністю до 0,001 маємо
і з точністю до 0,001 маємо  .
. називається число
називається число 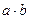 , яке задовольняє нерівності
, яке задовольняє нерівності  .
. з точністю до 0,1. Отримаємо
з точністю до 0,1. Отримаємо  ,значить, з точністю 0.1 маємо
,значить, з точністю 0.1 маємо  .
. і
і 
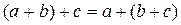 і
і 
 .
.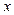 , називається модулемчисла. Записують так
, називається модулемчисла. Записують так  . Наприклад,
. Наприклад, 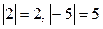 .
. , якщо воно розташовано лівіше на координатній прямій. Наприклад, 148>-2489, 214<6500.
, якщо воно розташовано лівіше на координатній прямій. Наприклад, 148>-2489, 214<6500. , що задовольняє умовам:
, що задовольняє умовам:

 .
.


