
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 1. Математичні поняття.Содержание книги
Поиск на нашем сайте
Лекція5. Поняття множини. Мета: Основні питання: 1. Поняття множини і елемента множини. 2. Способи завдання множин. 3. Відношення між множинами. 4. Множина і поняття. I. Поняття множини і елемента множини. В математиці часто приходиться розглядати певні групи об‘єктів як єдине ціле: числа від 1 до 10, натуральні числа, трикутники. Всі ці різноманітні сукупності називають множинами. Поняття множини являється одним з основних понять математики і тому не має означення через інші поняття. Його можна пояснити на прикладах: множина учнів класу, множина букв алфавіту, натуральні числа. В математиці розглядають множину, яка містить один об‘єкт, або не містить жодного елемента, яка називається пустою. Об‘єкти, з яких складається множина, називають його елементами. Часто приходиться з‘ясовувати належність елемента до розглянутої множини. Множини бувають скінчені і нескінчені. Скінченою множиною називають таку, елементи якої можна перерахувати. Нескінченими являються і множини чисел. II. Способи завдання множин. Вважають, що множина визначається своїми елементами, тобто множина задана, якщо про будь-який об‘єкт можна сказати, належить він цій множині чи не належить. Множину можна задати, перерахувавши всі його елементи. Наприклад, III. Відношення між множинами. Задані дві множини:
V. Множина і поняття. Як відомо, будь-яке поняття має об‘єм. З теоретик-множної позиції об‘єм поняття – це множина об‘єктів, які можна назвати одним словом, яке позначає поняття. Наприклад, об‘єм поняття «трикутник» - множина трикутників, об‘єм поняття «прямий кут» - множина прямих кутів. Підхід до об‘єму поняття як множині дає можливість наглядно уявити відношення між поняттями. Існують поняття, які не знаходяться в відношенні роду і виду. Наприклад, поняття «квадрат» і «трикутник» - їх об‘єми не знаходяться в відношенні включення.
Семестр Лекція 8. Поняття числа. Мета: ввести поняття натурального числа, розповісти історію виникнення поняття натурального числа, пояснити, що називають рахунком і його роль в побутовому житті. Розвивати пам‘ять, культуру мови усної і писемної. Основні питання: 1. Про історію виникнення натурального числа. 2. Порядкові і кількісні натуральні числа. Рахунок. 3. Рахунок. Теоретико – множний зміст кількісного числа і нуля.
Признаки подільності чисел. Ознака подільності на 2: Для того, щоб число
Ознака подільності на 5: Для того, щоб число Ознака подільності на 4: Для того, щоб число Ознака подільності на 3, 9: Для того, щоб число Ознака подільності на 10: Для того, щоб число Властивості НСД. 1. НСД завжди існує і являється єдиним. 2. НСД не перевищує меншого з даних чисел 3. НСД ділиться на кожний дільник цих чисел. Знову розглянемо числа 12 і 8 і випишемо декілька чисел, кратних ним: Спільним кратним чисел називається кожне натуральне число, яке кратне кожному з даних чисел. НСК називається найменше число з всіх спільних кратних даних чисел. Властивості НСК.
Теорема. Для будь-яких натуральних чисел Алгоритм Евкліда. Розглянемо на прикладі: Знайти Поділимо число 525 на 231 з залишком, маємо 525 Тобто Цей спосіб знаходження НСД засновано на діленні з залишком. Його першим описав давньогрецький математик Евклід (3ст. до н.е.).
Лекція 15,16. Дійсні числа. План: 1. Поняття ірраціонального додатного числа. 2. Дійсні числа, дії над ними. 3. Від‘ємні числа.
1. Поняття ірраціонального додатного числа. Дії над раціональними числами зручно виконувати, коли вони записані десятковими дробами. Тому краще і результати вимірів величин представляти в виді десяткових дробів. Якщо уявити процес десяткового виміру довжини відрізку в ідеалі(як це роблять в математиці), то можливі два варіанта: 1) на якомусь кроці процес виміру відрізку скінчиться. Тоді довжина відрізку Множину додатних ірраціональних чисел позначають
2. Дії над дійсними числами. Множина додатних дійсних чисел
Дії над додатними раціональними числами зводяться, в принципі, до дій над натуральними числами. Дії над нескінченими десятковими дробами можна звести до дій над раціональними, але необхідно ввести поняття приблизного значення дійсного числа за нестачею і залишком. Число Сумою дійсних чисел Наприклад, знайти суму двох чисел Добутком дійсних чисел Наприклад, обчислити добуток чисел Закони додавання і добутку дійсних чисел: 2) комутативний 3) асоціативний 4) дистрибутивний
3. Від’ємні числа. На координатній вісі усі точки, що стоять праворуч нуля являються додатними, а числа, що стоять ліворуч нуля називаються від’ємними. Числа, наприклад, 1 і -1 називають протилежними. Число нуль не являється ні додатним ні від’ємним. Усі точки координатної вісі відповідні дійсним числам. Множина дійсних чисел і координатна вісь знаходяться у взаємно однозначній відповідності: кожному дійсному числу відповідає єдина точка координатної прямої і навпаки. Відстань від нуля до точки, координата якої є число Дії над числами: 1. Порівняння дійсних чисел: число 2. Сумою двох дійсних чисел 1). Сума додатних чисел є число додатне; наприклад, 123+56=179 2). Сума від’ємних чисел є число від’ємне: додаємо модулі доданків і в переді ставимо знак мінус; наприклад, -12+(-45)=-57. 3). Сума чисел з різними знаками - це число, яке має знак такий, як і доданок з більшим модулем, а модуль суми – це різниця між доданками з більшим і меншим модулем, наприклад, 96+(-54)=42, -56+48=-8. 3. Добутком чисел 1). Добуток додатних чисел є число додатне, наприклад, 2). Добуток від’ємних чисел є число додатне; наприклад, 3). Добуток чисел з різними знаками є число від’ємне, наприклад,
4. Віднімання і ділення – це дії, обернені додаванню і множенню.
II курс I. Поняття функції. Функцією називається така залежність змінної Змінну III. Властивості функції. 4. монотонність. Функція називається зростаючою на деякому проміжку, якщо для будь-яких 5. парність. 6. перілдичність IV. Графік функції. Графічне зображення функції не тільки дозволяє уявити функціональну залежність наглядно, але надає можливість спростити вивчення її властивостей. Тому навіть в тому випадку, якщо функція задана аналітично, часто звертаються до її графіку на координатній площині. Графіком функції
Означення рівняння. Рівність, яка містить невідоме число, позначене буквою, називають рівнянням. Наприклад,
Розв‘язати рівняння – значить знайти всі ті значення невідомого, при яких рівняння перетворюються в вірну рівність (тотожність). Всі такі значення невідомого називають коренями (розв‘язками) рівняння.
*Рівняння може мати єдиний корінь
Підставивши інше значення отримаємо невірну рівність. *Рішення може мати декілька коренів
*Рішення може зовсім не мати коренів
*Рішення може мати нескінченну множину коренів
Яке б значення
Рівносильні рівняння. Корені рівняння
Два рівняння називаються рівносильними, якщо кожен з них має ті ж корні, що і інше
обидва рівняння не мають жодного кореня але вважаються рівносильними
Властивості рівнянь. * Якщо до обох частинрівняння додати одне й теж саме число чи багаточлен, то нове рівняння буде рівносильна заданому.
*Якщо обидві частини рівняння помножити на одне і теж число
Користуючись цими двома властивостями можна розв‘язувати рівняння, не звертаючись на залежність між заданим і результатами арифметичних дій.
Класифікація рівнянь. 1. рівняння називають алгебраїчним, якщо права і ліва частини багаточлени
2. дробово-раціональними, якщо хоча б одна частина дробово-раціональна відносно невідомої.
3. ірраціональне, якщо хоча б одна частина містить ірраціональну залежність відносно
4. трансцендентне, якщо
Лінійні рівняння. Рівняння виду Очевидно, такому рівнянню еквівалентні 1. якщо 2. 3.
Квадратні рівняння. Рівняння Якщо 1.
2.
3. Корені повного квадратного рівняння обчислюють за формулою;
Теорема Вієта
Теорема
Семестр Геометричні фігури. Геометрія – це наука про властивості геометричних фігур. Слово «геометрія» грецьке, в перекладі – «земле вимірювання». Геом.. фігури бувають досить різноманітні. Будь – яку геом.. фігуру можна представити складену з точок. Планіметрія – це розділ геометрії, в якому вивчають фігури на площині. Основними геом.. фігурами на площині являються точка і пряма. Пряма нескінченна. (Кажуть, що точки лежать на прямій, або належать, а пряма проходить через точки. Прямі перетинаються в точці, або точка А – точка перетину прямих. Її зображення і аксіоми). Відрізком називається частина прямої, яка складається з всіх точок цієї прямої, які лежать між двома заданими точками. Ці точки називають кінцями відрізка. Кути, їх види, побудова. Кутом називається фігура, яка складається з точки (вершини кута) і двох різних прямих, які виходять з цієї точки(сторін кута). Якщо сторони кута лежать на одній прямій і розміщені по різні боки від вершини, то кут називається розгорнутим. Кути вимірюються в градусах за допомогою транспортира. А) кожний кут має певну градусну міру, більшу від нуля. Розгорнутий кут - А) на будь-якій пів прямій від її початкової точки можна відкласти відрізок заданої довжини, і тільки один. На кожній пів прямій зв задану півплощину можна відкласти кут із заданою градусною мірою, іф тільки один. Суміжні кути: два кути називаються суміжними, якщо у них одна сторона спільна, дві інші лежать на одній прямій, по різні сторони вершини. Теорема. Сума мір суміжних кутів дорівнює Якщо два кути рівні, то суміжні з ними кути рівні. кут, міра якого 90 градусів називається прямим. Кут, градусна міра якого менша 90 градусів – гострий. Вертикальні кути: два кути називаються вертикальними, якщо сторони одного кута являються додатковими промінами сторін другого. Теорема. Вертикальні кути рівні. Перпендикуляр до прямої. Дві прямі називають перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема. Через кожну точку прямої можна провести перпендикулярну їй пряму і тільки одну. Перпендикуляром до прямої називається відрізок прямої, перпендикулярної заданій, який має одним з своїх кінців їх точку перетину. Цей кінець називається основою перпендикуляра. Лекція 1. Математичні поняття. Мета: Основні питання: 1. Вступ. 2. Об‘єм і зміст поняття. 3. Означення понять. 4. Вимоги до означення понять. I. Вступ. Математика, як і інші науки, вивчає навколишнє середовище, природні та суспільні явища, але вивчає лише їх з особливого боку. Наприклад, в геометрії вивчають форму і розміри предметів, не враховуючи інші властивості: колір, масу і т.д. тому в геометрії замість слова «предмет» кажуть: «геометрична фігура». Відрізок, промінь, пряма, кут, коло, квадрат – геометричні фігури. Результатом абстрагування являються також найважливіші математичні поняття, як «число» і «величина». Взагалі будь-які математичні об‘єкти – це результат відокремлення з предметів і явищ навколишнього середовища кількісних і просторових властивостей і відношень і абстрагування їх від всіх інших властивостей. Як сказав Ф. Енгельс: «математика – це наука про кількісні форми і просторові уявлення реального світу». Математичні об‘єкти реально не існують, не існує в навколишньому світі геометричних фігур, чисел. Всі вони утворені людьми в процесі історичного розвитку суспільства і існує лише в розумінні людини і в тих знаках і символах, які утворюють математичну мову. II. Об‘єм і зміст поняття. Будь – який математичний об‘єкт має певні властивості. Наприклад, квадрат має чотири сторони, чотири прямих кута, рівні діагоналі. Можна вказати і інші властивості квадрата. Серед властивостей об‘єкта розрізнюють властивості суттєві і несуттєві для його виділення з інших об‘єктів. Властивість вважають суттєвою для об‘єкта, якщо вона притаманна цьому об‘єкту і без нього він не може існувати. Несуттєвими властивостями вважають такі, відсутність яких не впливає на існування об‘єкта. Щоб розуміти, що представляє собою даний об‘єкт достатньо знати його суттєві властивості. В цьому випадку кажуть, що мають поняття про цей об‘єкт. Сукупність всіх взаємозв’язаних суттєвих властивостей об‘єкта називають змістом поняття про цей об‘єкт. Об‘єм поняття – це сукупність всіх об‘єктів, які позначені одним терміном. Таким чином, всяке поняття характеризується терміном, об‘ємом і змістом. Між об‘ємом поняття і його змістом існує зв‘язок: чим «більше» об‘єм поняття, тим «менше»його зміст, і навпаки. Наприклад, об‘єм поняття «прямокутний трикутник» «менше» об’єму поняття «трикутник», оскільки в об‘єм першого поняття входять не всі трикутники, а тільки прямокутні. Але зміст першого поняття «більше» змісту другого: прямокутний трикутник має не лише всі властивості трикутника, але і іншими, які притаманні тільки прямокутним трикутникам. III. Означення понять. Зміст поняття о будь-яком математичному об‘єкті містить багато різних суттєвих властивостей цього об‘єкта. Але щоб встановити, чи міститься об‘єкт в об‘ємі даного поняття (тобто разпознати його), необхідно перевірити наявність у нього лише деяких суттєвих властивостей. Встановлення цих суттєвих властивостей об‘єкта, яких достатньо для распознавння об‘єкта, називається означенням поняття про цей об‘єкт. Взагалі, означення – це логічна операція, яка розкриває зміст поняття. Способи означення поняття є різні. Перед усім розрізняють явні і неявні означення. Явні поняття мають форму рівності, спів падіння двох понять, або ототожнюються два поняття. Одне з них називають визначним поняттям, друге – визначальним. Ч ерез визначальне розкривається зміст визначного поняття. Проаналізуємо, наприклад, структуру означення квадрата: «Квадратом називається прямокутник, у якого всі сторони рівні». Вона є такою: спочатку вказане визначне поняття – «квадрат», а потім приведене визначальне, яке включає властивості: бути прямокутником, мати всі рівні сторони. Властивість «бути прямокутником» показує, що всі квадрати являються прямокутниками, тобто поняття прямокутник являється більш загальним, ніж поняття квадрат. Його називають родовим по відношенню до визначного поняття «квадрат». Друга властивість – «мати рівні сторони» - це виділення видової властивості, яка відокремлює квадрат від інших видів прямокутника. Схематично структуру таких означень можна представити наступним чином: МАЛЮНОК. Неявні означення не мають форми спів падіння двох понять. Прикладами таких означень являються так звані контекстуальні і остенсивні означення. В контекстуальних означеннях зміст нового поняття розкривається через уривок тексту, через контекст, через аналіз конкретної ситуації, яка описує зміст нового поняття. Прикладом такого означення може бути означення рівняння і його розв‘язок. Остенсивні означення використовують для введення термінів шляхом демонстрації об‘єктів, які цими термінами позначають. Тому остенсивні означення називають ще означеннями шляхом показу. Зустрічаються в математиці і означення, побудовані по іншому. Наприклад, означення трикутника: «Трикутником називається фігура, яка складається з трьох точок. Які не лежать на одній прямій, і трьох відрізків, які попарно з‘єднують ці точки». В цьому означенні вказане родове поняття по відношенню до трикутника – фігура, а потім вказаний спосіб побудови такої фігури, такі означення називають генетичними. Розглянемо означення арифметичної прогресії: «Арифметичною прогресією називається числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому, доданого з одним числом». Тут визначне поняття – «арифметична прогресія», родове поняття – «числова послідовність», а далі описується спосіб отримання всіх членів прогресії по заданій формулі. Таке означення називають індуктивним (рекурентним). IV. Вимоги до означень. Щоб оцінити правильність явних означень, необхідно знати правила означення понять.1) Перш за все визначне і визначальне поняття повинні бути еквівалентні (сорозмірні). Це означає, що сукупність предметів, які є охоплені ними, мають співпадати. Наприклад, правильним є означення: «прямокутник – це чотирикутник, у якого всі кути прямі». Неправильним означенням є таке:»Прямі
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.238.161 (0.013 с.) |

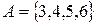 . Якщо множина нескінчена, то її елементи перерахувати не можна. В таких випадках вказують характеристичну властивість його елементів. Характеристична властивість – це така властивість, якою володіє кожний елемент, який належить множині, і не володіє жоден з елементів, який йому не належить. Для того щоб задати деяку множину, достатньо або перерахувати всі його елементи, або вказати характеристичну властивість його елементів. Наприклад, множина А натуральних чисел, менших 7, задана вказанням характеристичної властивості його елементів, можна задати і так:
. Якщо множина нескінчена, то її елементи перерахувати не можна. В таких випадках вказують характеристичну властивість його елементів. Характеристична властивість – це така властивість, якою володіє кожний елемент, який належить множині, і не володіє жоден з елементів, який йому не належить. Для того щоб задати деяку множину, достатньо або перерахувати всі його елементи, або вказати характеристичну властивість його елементів. Наприклад, множина А натуральних чисел, менших 7, задана вказанням характеристичної властивості його елементів, можна задати і так: 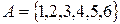 , тобто перерахував його елементи.
, тобто перерахував його елементи.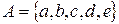 і
і  . Видно, що елементи
. Видно, що елементи 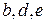 належать одночасно множині А і В. кажуть, що ці елементи – спільні для множин А і В, а самі множини перетинаються. Якщо множини не мають спільних елементів, то говорять, що вони не перетинаються. Множини
належать одночасно множині А і В. кажуть, що ці елементи – спільні для множин А і В, а самі множини перетинаються. Якщо множини не мають спільних елементів, то говорять, що вони не перетинаються. Множини  перетинаються, причому, кожний елемент множини В являється елементом множини А. в цьому випадку говорять, що множина В включена в А або що множина В являється підмножиною множини А. Множина В називається підмножиною множини А, якщо кожний елемент множини В належить множині А, і записують
перетинаються, причому, кожний елемент множини В являється елементом множини А. в цьому випадку говорять, що множина В включена в А або що множина В являється підмножиною множини А. Множина В називається підмножиною множини А, якщо кожний елемент множини В належить множині А, і записують 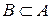 . Серед всіх підмножин заданої множини повинні бути обов‘язково пуста множина і сама множина. Якщо множини перетинаються, причому кожний елемент множини А являється елементом множини В, і навпаки, кожний елемент множини В являється елементом множини А, то говорять, що множини А і В є рівними. Тобто множини А і В називаються рівними, якщо
. Серед всіх підмножин заданої множини повинні бути обов‘язково пуста множина і сама множина. Якщо множини перетинаються, причому кожний елемент множини А являється елементом множини В, і навпаки, кожний елемент множини В являється елементом множини А, то говорять, що множини А і В є рівними. Тобто множини А і В називаються рівними, якщо 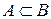 , записують
, записують  . З означення випливає, що рівні множини складаються з однакових елементів і що порядок запису елементів множини не являється суттєвим. Наглядно відношення між множинами зображають за допомогою особливих малюнків, які називають кругами Ейлера. Поняття множини і підмножини в початковій математиці в явній формі не вивчається, але задач, пов‘язаних з виділенням деякої сукупності, учні розв‘язують багато. Наприклад, «серед даних чотирикутників вказати прямокутники», «назвати серед даних чисел парні».
. З означення випливає, що рівні множини складаються з однакових елементів і що порядок запису елементів множини не являється суттєвим. Наглядно відношення між множинами зображають за допомогою особливих малюнків, які називають кругами Ейлера. Поняття множини і підмножини в початковій математиці в явній формі не вивчається, але задач, пов‘язаних з виділенням деякої сукупності, учні розв‘язують багато. Наприклад, «серед даних чотирикутників вказати прямокутники», «назвати серед даних чисел парні». ділилося на 2, необхідно і достатньо, його десятковий запис закінчувався цифрою 0,2,4,6,8.
ділилося на 2, необхідно і достатньо, його десятковий запис закінчувався цифрою 0,2,4,6,8. і
і  . У чисел 12 і 8 існують спільні кратні – 24,48,72,…. Серед них є найменше число 24. його називають найменшим спільним кратним НСК.
. У чисел 12 і 8 існують спільні кратні – 24,48,72,…. Серед них є найменше число 24. його називають найменшим спільним кратним НСК. добуток їх НСК і НСД дорівнює добутку чисел
добуток їх НСК і НСД дорівнює добутку чисел  . Ця рівність дозволяє знайти НСК по відомому значення НСД.
. Ця рівність дозволяє знайти НСК по відомому значення НСД. .
. 231=
231=  , дільник 231 поділимо на залишок 63, отримаємо 231=
, дільник 231 поділимо на залишок 63, отримаємо 231=  , аналогічно дільник 63 поділимо на залишок 42, 63=
, аналогічно дільник 63 поділимо на залишок 42, 63=  , потім число 42 ділимо на 21 - 42=
, потім число 42 ділимо на 21 - 42=  . Останній відмінний від нуля дільник при послідовному діленні і являється НСД заданих чисел 525 і 231.
. Останній відмінний від нуля дільник при послідовному діленні і являється НСД заданих чисел 525 і 231. =
=  =
= 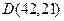 =
=  =21,значить
=21,значить  .
. буде виражена скінченим десятковим дробом виду
буде виражена скінченим десятковим дробом виду  . 2) описаний процес виміру довжини відрізку нескінчений. Тоді його представляють символом
. 2) описаний процес виміру довжини відрізку нескінчений. Тоді його представляють символом 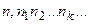 , який називають нескінченим періодичним дробом. Існують відрізки, довжина яких не являються періодичним десятковим дробом, тобто раціональним числом, при вибраній одиниці виміру. Такі нескінчені неперіодичні десяткові дроби називають додатними ірраціональними числами. Ірраціональні числа можна отримати і при знаходженні радикалів із деяких раціональних чисел, наприклад
, який називають нескінченим періодичним дробом. Існують відрізки, довжина яких не являються періодичним десятковим дробом, тобто раціональним числом, при вибраній одиниці виміру. Такі нескінчені неперіодичні десяткові дроби називають додатними ірраціональними числами. Ірраціональні числа можна отримати і при знаходженні радикалів із деяких раціональних чисел, наприклад  , а також ірраціональними є числа
, а також ірраціональними є числа 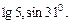 числа
числа 
 .
. - це об‘єднання множини додатних раціональних чисел і множини додатних ірраціональних чисел. Тому будь-яке дійсне число можна представити в виді нескінченого десяткового дробу – періодичного, якщо воно раціональне, або неперіодичного, якщо воно ірраціональне.
- це об‘єднання множини додатних раціональних чисел і множини додатних ірраціональних чисел. Тому будь-яке дійсне число можна представити в виді нескінченого десяткового дробу – періодичного, якщо воно раціональне, або неперіодичного, якщо воно ірраціональне. має приблизним значенням за нестачею з точністю до
має приблизним значенням за нестачею з точністю до  таке число
таке число  (тобто це число отримаємо, якщо залишимо цілу частину числа
(тобто це число отримаємо, якщо залишимо цілу частину числа  називають число
називають число  (тобто це число отримаємо, якщо в запису
(тобто це число отримаємо, якщо в запису  називається число
називається число  , яке задовольняє нерівності
, яке задовольняє нерівності  .
. з точністю до 0,001. Розглянемо їх приблизні значення
з точністю до 0,001. Розглянемо їх приблизні значення  , отже
, отже  і з точністю до 0,001 маємо
і з точністю до 0,001 маємо  .
. називається число
називається число 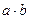 , яке задовольняє нерівності
, яке задовольняє нерівності  .
. з точністю до 0,1. Отримаємо
з точністю до 0,1. Отримаємо  ,значить, з точністю 0.1 маємо
,значить, з точністю 0.1 маємо  .
. і
і 
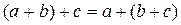 і
і 
 .
.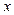 , називається модулемчисла. Записують так
, називається модулемчисла. Записують так  . Наприклад,
. Наприклад, 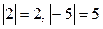 .
. , якщо воно розташовано лівіше на координатній прямій. Наприклад, 148>-2489, 214<6500.
, якщо воно розташовано лівіше на координатній прямій. Наприклад, 148>-2489, 214<6500. , що задовольняє умовам:
, що задовольняє умовам:

 .
. від змінної
від змінної  , при якій кожному значенню
, при якій кожному значенню 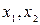 виконується умова
виконується умова  . Функція називається спадною, якщо для будь-яких
. Функція називається спадною, якщо для будь-яких  .
. , заданої на множині
, заданої на множині  , називається множина таких точок координатної площини, які мають координати
, називається множина таких точок координатної площини, які мають координати  для всіх значень
для всіх значень  ,
,  , або
, або .
.

 - невірна рівність
- невірна рівність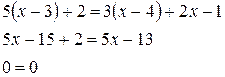

 не рівносильні
не рівносильні являються рівносильними
являються рівносильними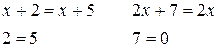

 , то нове рівняння буде рівносильне заданому.
, то нове рівняння буде рівносильне заданому.




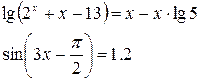
 називають лінійними
називають лінійними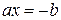
 існує єдиний корінь
існує єдиний корінь не має жодного кореня
не має жодного кореня нескінченно багато коренів
нескінченно багато коренів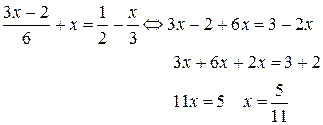
 називають квадратними, якщо
називають квадратними, якщо  , то рівняння
, то рівняння 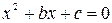 називають зведеним,
називають зведеним, рівняння називається повним, в іншому випадку неповним
рівняння називається повним, в іншому випадку неповним





 ,
,  . Градусна міра кута дорівнює сумі мір кутів, на які він розбивається будь-яким променем, який проходить крізь його сторони.
. Градусна міра кута дорівнює сумі мір кутів, на які він розбивається будь-яким променем, який проходить крізь його сторони. називаються паралельними, якщо вони не мають спільних точок або співпадають» (занадто широко, тому що йому задовольняють і мимобіжні прямі). Або невірним є: «прямі
називаються паралельними, якщо вони не мають спільних точок або співпадають» (занадто широко, тому що йому задовольняють і мимобіжні прямі). Або невірним є: «прямі  » (недостатньо властивостей). 4) Ще одне правило до означення – відсутність в ньому збитку. Це позначає, що в означенні не повинно бути вказано зайвих властивостей, які випливають з інших властивостей, також включених в означення поняття. Наприклад, «прямокутником називається чотирикутник, у якого всі сторони рівні і всі кути прямі».це означення має зайву властивість, краще сказати так: «Прямокутником називається чотирикутник, у якого всі кути прямі». Треба сказати, що в будь-якому означенні є елемент довільності, що проявляється, по-перше, в виборі терміна, а по-друге, в виборі властивостей, які включаються в означення. Якщо одному поняття дається два різних означення, то вони повинні бути рівносильними. Це позначає, що з властивостей, що включені в одне означення, мають випливати властивості, покладені в основу другого означення, і навпаки. При виборі означення користуються тим, яке означення простіше, натуральніше або корисніше для подальшої побудови теорії.
» (недостатньо властивостей). 4) Ще одне правило до означення – відсутність в ньому збитку. Це позначає, що в означенні не повинно бути вказано зайвих властивостей, які випливають з інших властивостей, також включених в означення поняття. Наприклад, «прямокутником називається чотирикутник, у якого всі сторони рівні і всі кути прямі».це означення має зайву властивість, краще сказати так: «Прямокутником називається чотирикутник, у якого всі кути прямі». Треба сказати, що в будь-якому означенні є елемент довільності, що проявляється, по-перше, в виборі терміна, а по-друге, в виборі властивостей, які включаються в означення. Якщо одному поняття дається два різних означення, то вони повинні бути рівносильними. Це позначає, що з властивостей, що включені в одне означення, мають випливати властивості, покладені в основу другого означення, і навпаки. При виборі означення користуються тим, яке означення простіше, натуральніше або корисніше для подальшої побудови теорії.


