
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 6, 7. Дії над множинами.Содержание книги
Поиск на нашем сайте
Мета: Основні питання: 1. Перетин множин. 2. Об‘єднання множин. 3. Закони перетину і об‘єднання множин. 4. Доповнення підмножини. 5. Поняття розбиття множин на класи. 6. Задачі, пов‘язані з операціями над скінченими множинами. 7. Декартовий добуток множин. 8. Зображення декартового добутку множин на координатній площині. I. Перетин множин. З елементів двох і більше множин можна утворити нові множини. Вважають, що ці нові множини являються результатом операцій над множинами. Нехай задані дві множини: II. Об‘єднання множин. Об‘єднанням множин А і В називається множина, яка містить тільки такі елементи, які належать множині А або множині В. позначають III. Закони перетину і об‘єднання множин. З означень перетину і об‘єднання множин випливає для будь-яких множин А і В справедливість рівностей
IV. Доповнення підмножини. Щоб пояснити учням, що 5-2=3, часто використовують такий прийом. Беруть 5 предметів (кружків), після того, як учні впевняться за допомогою рахунку, що кружечків дійсно 5, їм пропонують 2 кружечка прибрати і порахувати, скільки кружечків залишилося – 2. Нехай V. Поняття розбиття множин на класи. Поняття множини і операцій над множинами дозволяє уточнити наше уявлення про класифікацію. Класифікація – це дія розподілу об‘єктів по класам на основі схожостей об‘єктів в самому класі і їх відмінності від об‘єктів інших класів. Як правило, метою класифікації являється систематизація наших знань. Наприклад, натуральні числа поділяються на парні і непарні; кути бувають гострі, прямі і тупі. Будь-яка класифікація пов‘язана з розбиттям деякої множини на підмножини. Вважають, що множина А розбита на класи
VI. Задачі, пов‘язані з операціями над скінченими множинами. В математиці часто приходиться розв‘язувати задачі, в яких треба визначити число елементів або в множині, або в об‘єднанні множин, або в доповненні підмножин. Існують певні прийоми розв‘язку таких задач. Умовимось позначати число елементів скінченої множини А VI. Декартовий добуток множин. В початкових класах учні розв’язують задачу: «Використовуючи цифри 1,2,3 утворіть всілякі двозначні числа». Такими являються 11,12,13,21,22,23,31,32,33. такі пари чисел впорядковані (важливий порядок слідування елементів). Впорядковану пару елементів Декартовим добутком множин А і В називається множина пар, перша компонента якої належить множині А, друга – множині В. Позначають Властивості: 1. анти комутативність: 2. анти асоціативність: 3. дистрибутивність до об‘єднання: Елементи декартового добутку двох скінчених множин зручно записувати за допомогою таблиці. Наприклад, (МАЛЮНОК). В математиці розглядають впорядковані набори з 3,4,5…елементів, які називають кортежами. Наприклад, (1,5,6) – кортеж довжини 3, (2,0,7,8,9,4) – кортеж довжиною 6. Декартовим добутком множин Наприклад, VIII. Зображення декартового добутку множин на координатній площині
Скінчені множини, які містять невелику кількість елементів, зобразити їх декартовим добуток неважко. А якщо ж множини А і В нескінчені? Круги Ейлера в цьому випадку не допоможуть. Але декартовим добуток можна зобразити на координатній площині. Координатна пряма – це пряма із заданим на ній початком відліку і додатнім напрямком. (МАЛЮНОК). З введенням координатної прямої встановлюється зв‘язок між точками прямої і дійсними числами: кожній точці М прямої відповідає єдине дійсне число Х – координата цієї точки, і навпаки. Розглянемо дві взаємно перпендикулярні координатні прямі: ох – абсцис і оу – ординат, з спільним початком і одиницями довжини. Площину, в якій побудовані такі вісі називають координатною площиною. ПДСК дозволяє кожній точці площини поставити в відповідність єдину пару дійсних чисел – координат цієї точки, і навпаки. З введенням координат на прямій чи на площині з‘явилась можливість розв‘язувати багато геометричних задач засобами алгебри і навпаки, алгебраїчні задачі розв‘язувати наглядно. Поняття ПДСК і координат було введено в геометрії французьким вченим і філософом Рене Декартом в XVII столітті. Припустимо, множини А і В – числові. Тоді елементами декартового добутку цих множин будуть впорядковані пари чисел. Якщо зобразити кожну пару чисел точкою на координатній площині, то отримаємо фігуру, яка буде наглядно представляти декартовим добуток ТЕОРЕМА. Я кщо множина А містить Правило підрахунку числа елементів декартового добутку широко використовується при розв‘язанні комбінаторних задач.
Семестр Лекція 8. Поняття числа. Мета: ввести поняття натурального числа, розповісти історію виникнення поняття натурального числа, пояснити, що називають рахунком і його роль в побутовому житті. Розвивати пам‘ять, культуру мови усної і писемної. Основні питання: 1. Про історію виникнення натурального числа. 2. Порядкові і кількісні натуральні числа. Рахунок. 3. Рахунок. Теоретико – множний зміст кількісного числа і нуля.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.208.27 (0.01 с.) |

 і
і  . Утворимо множину С, в яку включимо спільні елементи множин А і В:
. Утворимо множину С, в яку включимо спільні елементи множин А і В:  . Отриману множину С називають перетином множин А і В. Перетином множин А і В називається множина, яка містить тільки ті елементи, які належать множині А і множині В. Позначають
. Отриману множину С називають перетином множин А і В. Перетином множин А і В називається множина, яка містить тільки ті елементи, які належать множині А і множині В. Позначають  і зображають МАЛ. В тому випадку, коли множини А і В не мають спільних елементів, говорять, що їх перетином являється пуста множина. Операція, за допомогою якої знаходять перетин множин, називається перетином. Згідно означенню перетину
і зображають МАЛ. В тому випадку, коли множини А і В не мають спільних елементів, говорять, що їх перетином являється пуста множина. Операція, за допомогою якої знаходять перетин множин, називається перетином. Згідно означенню перетину  . Якщо елементи множин А і В перелічені, то щоб знайти їх перетин, достатньо перелічити їх спільні елементи. Якщо множини задані за допомогою характеристичною властивістю, то з означення перетину випливає, що ця характеристична властивість перетину складається з характеристичних властивостей заданих множин за допомогою союзу «і».
. Якщо елементи множин А і В перелічені, то щоб знайти їх перетин, достатньо перелічити їх спільні елементи. Якщо множини задані за допомогою характеристичною властивістю, то з означення перетину випливає, що ця характеристична властивість перетину складається з характеристичних властивостей заданих множин за допомогою союзу «і».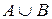 і зображають МАЛ. Операція, за допомогою якої знаходять об‘єднання множин, називається об‘єднанням. Згідно означенню об‘єднання
і зображають МАЛ. Операція, за допомогою якої знаходять об‘єднання множин, називається об‘єднанням. Згідно означенню об‘єднання  . Якщо елементи множин А і В перелічені, то для того, щоб знайти їх об‘єднання, достатньо перелічити елементи, які належать хоча б одній множині. Наприклад,
. Якщо елементи множин А і В перелічені, то для того, щоб знайти їх об‘єднання, достатньо перелічити елементи, які належать хоча б одній множині. Наприклад,  . Якщо ж множини задані за допомогою характеристичної властивості їх елементів, то із означення об‘єднання випливає, що характеристична властивість об‘єднання складається з характеристичних властивостей множин А і В за допомогою союзу «або».
. Якщо ж множини задані за допомогою характеристичної властивості їх елементів, то із означення об‘єднання випливає, що характеристична властивість об‘єднання складається з характеристичних властивостей множин А і В за допомогою союзу «або». і
і  , які представляють собою запис комутативного закону для перетину і об‘єднання множин. Для перетину і об‘єднання множин справедливі також асоціативні закони: для будь-яких множин А, В і С виконуються рівності
, які представляють собою запис комутативного закону для перетину і об‘єднання множин. Для перетину і об‘єднання множин справедливі також асоціативні закони: для будь-яких множин А, В і С виконуються рівності  і
і 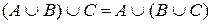 . Наглядно уявити асоціативний закон можна за допомогою кругів Ейлера, а також провести доведення цих законів. Це пояснює, як знаходити перетин і об‘єднання трьох множин, якщо відомо правило для двох множин. Комутативний і асоціативний закони множин можна розповсюджувати на будь-яку кількість множин. Дистрибутивний закон: для будь-яких множин А, В і С справедливі рівності
. Наглядно уявити асоціативний закон можна за допомогою кругів Ейлера, а також провести доведення цих законів. Це пояснює, як знаходити перетин і об‘єднання трьох множин, якщо відомо правило для двох множин. Комутативний і асоціативний закони множин можна розповсюджувати на будь-яку кількість множин. Дистрибутивний закон: для будь-яких множин А, В і С справедливі рівності  і
і  . Якщо в виразі існують знаки перетину і об‘єднання і не існує дужок, то спочатку виконують перетин, так як вважають, що операція перетину більш «сильна», ніж об‘єднання.
. Якщо в виразі існують знаки перетину і об‘єднання і не існує дужок, то спочатку виконують перетин, так як вважають, що операція перетину більш «сильна», ніж об‘єднання.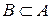 . Доповненням множини В до множини А називається множина, яка містить ті елементи множини А, які не належать множині В. позначають
. Доповненням множини В до множини А називається множина, яка містить ті елементи множини А, які не належать множині В. позначають  . Операція, за допомогою якої знаходять доповнення підмножини, називається відніманням. Згідно з означенням доповнення
. Операція, за допомогою якої знаходять доповнення підмножини, називається відніманням. Згідно з означенням доповнення  . Якщо елементи множин А і В перелічені, то для того, щоб знайти
. Якщо елементи множин А і В перелічені, то для того, щоб знайти  , а
, а  , то
, то  . В тому випадку, коли вказані характеристичні властивості елементів множин А і В, характеристична властивість множини
. В тому випадку, коли вказані характеристичні властивості елементів множин А і В, характеристична властивість множини  ». В запису множини
». В запису множини  нема дужок, тому (вважають, що операція перетину множин являється більш «сильною», ніж віднімання) спочатку виконують перетин множин В і С, а потім отриману множину віднімають з множини А..
нема дужок, тому (вважають, що операція перетину множин являється більш «сильною», ніж віднімання) спочатку виконують перетин множин В і С, а потім отриману множину віднімають з множини А..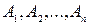 , якщо: 1) підмножини
, якщо: 1) підмножини 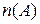 . Якщо задані скінчені множини А і В, які перетинаються, то кількість елементів в їх об‘єднанні підраховують за формулою
. Якщо задані скінчені множини А і В, які перетинаються, то кількість елементів в їх об‘єднанні підраховують за формулою 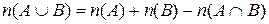 . Якщо ж множини А і В не мають спільних елементів, то число елементів в їх об‘єднанні визначають так:
. Якщо ж множини А і В не мають спільних елементів, то число елементів в їх об‘єднанні визначають так:  . Неважко впевнитися в тому, що якщо
. Неважко впевнитися в тому, що якщо  . Розглянемо задачу: «З 40 учнів класу 34 вивчають німецьку мову, 23 – англійську, 17 – і німецьку і англійську. Чи є в класі учні, які не вивчають ні німецьку, ні англійську мови?». Відповідь: нема жодного учня в класі, який би не вивчав іноземні мови.
. Розглянемо задачу: «З 40 учнів класу 34 вивчають німецьку мову, 23 – англійську, 17 – і німецьку і англійську. Чи є в класі учні, які не вивчають ні німецьку, ні англійську мови?». Відповідь: нема жодного учня в класі, який би не вивчав іноземні мови. позначають
позначають  , де
, де  - перша координата (компонента),
- перша координата (компонента),  - друга. Дві пари рівні, якщо
- друга. Дві пари рівні, якщо  при
при  . Можна утворити впорядковані пари з елементів різних множин. Наприклад,
. Можна утворити впорядковані пари з елементів різних множин. Наприклад, 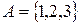 і
і  , тоді
, тоді  - утворили нову множину.
- утворили нову множину. .
. .
. .
. .
. називається множина кортежем довжини
називається множина кортежем довжини 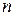 , які утворені так, що перша координата належить множині
, які утворені так, що перша координата належить множині 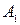 , друга -
, друга -  ,…, остання -
,…, остання -  . Позначають
. Позначають  .
. ,
,  ,
,  , тоді
, тоді  .
. ,
,  і
і  і
і  . (МАЛ.)
. (МАЛ.) елементів, а множина В -
елементів, а множина В -  елементів. Тобто, якщо
елементів. Тобто, якщо  ,
, 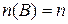 , то
, то  .
.


