
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема побудови розв’язку диференційного рівняння з частинними похіднимиСодержание книги
Поиск на нашем сайте Наведемо схему побудови розв’язку диференційного рів-няння з частинними похідними, де шукана функція
де
П.У. К.У.
де Задача (7.2) – (7.3) нестаціонарна, оскільки шуканий роз-в’язок істотно залежить від початкових умов і описує так званий неусталений перехідний режим фізичного процесу. Застосуємо перетворення Лапласа до функції
Тут Для знаходження зображень частинних похідних по
Вважатимемо, що
де Таким чином, вважаючи, що
з крайовими умовами (7.4), де
Приклад 7.1 Кінці струни
яке задовольняє задані додаткові умови П.У. Застосуємо перетворення Лапласа до функції
Тоді на основі цих співвідношень та сформульованої зада-чі з додатковими умовами, одержимо у просторі зображень наступну задачу
К.У.
Розв’язок лінійного неоднорідного диференціального рівняння другого порядку шукаємо у вигляді:
де Характеристичне рівняння
Тоді загальний розв’язок однорідного рівняння буде
Частинний розв’язок неоднорідного рівняння Для знаходження невідомої сталої
Звідси
Тоді
Загальний розв’язок рівняння буде мати вигляд:
Підставляючи розв’язок у крайові умови, знайдемо невідомі константи
Отже, оригіналом для
буде функція
яка є розв’язком поставленої задачі.
Приклад 7.2 Знайти розв’язок рівняння теплопровідності
П.У.
Застосуємо перетворення Лапласа до функції
Вихідне рівняння після підстановки отриманих формул та крайові умови у просторі зображень набудуть вигляду
К.У.
Розв’язок отриманого лінійного неоднорідного диференціального рівняння другого порядку шукатимемо у вигляді:
де
характеристичне рівняння:
Звідси
Тоді загальний розв’язок однорідного рівняння буде
Частинний розв’язок неоднорідного рівняння
Для знаходження невідомої сталої
Звідси
Тоді,
Загальний розв’язок рівняння буде мати вигляд:
Підставляючи розв’язок у крайові умови, знайдемо невідомі константи
Отже, оригіналом для
буде функція
яка і буде розв’язком поставленої задачі.
Контрольні запитання 7.1 Як використовуються операційні методи при розв’язуванні диференціальних рівнянь з частинними похідними? 7.2 Що називається оригіналом та зображенням функції-оригіналу 7.3 Що називають перетворенням Лапласа функції 7.4 Властивості зображень. 7.5 Зображення згортки. Властивість згортки. 7.6 Схема побудови розв’язку диференціального рівняння з частинними похідними.
Перелік використаних джерел 1. Араманович И.Г. Уравнения математической физики / И.Г. Араманович, В.И. Левин. – М.: Наука, 1964. – 286 с. 2. Владимиров В.С. Уравнения математической физики / В.С. Владимиров. – М.: Наука, 1967. – 436 с. 3. Кальницкий Л.А. Специальный курс высшей математики / Л.А. Кальницкий, Д.А. Добротин, В.Ф. Жевержеев. – М.: Высшая школа, 1976. – 389 с. 4. Кошляков Н.С. Уравнения в частных производных математической физики / Н.С. Кошляков, Э.Б. Глинер, М.М. Смирнов. – М.: Высшая школа, 1970. – 710 с. 5. Краснов М.Л. Функции комплексного переменного. Операционное исчисление. Теория устойчивости / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. – М.: Наука, 1971. – 256 с. 6. Полянин А.Д. Справочник по линейным уравнениям мате- матической физики / А.Д. Полянин. – М.: физматлит, 2001. – 576 с. 7. Смирнов М.М. Задачи по уравнениям математической фи- зики / М.М. Смирнов. – М.: Наука, 1975. – 126 с. 8. Чинаев П.И. Высшая математика. Специальные главы / П.И. Чинаев, А.А. Черенков, Н.А. Минин, А.Ю. Перевозни-ков. – К.: Вища школа, 1977. – 368 с.
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

 за-лежить лише від двох змінних
за-лежить лише від двох змінних  і
і  . Нехай вона задовольняє рівняння:
. Нехай вона задовольняє рівняння: , (7.2)
, (7.2) – неперервні функції від
– неперервні функції від  . Нехай треба знайти розв’язок рівняння (7.2)
. Нехай треба знайти розв’язок рівняння (7.2)  , що задово-льняє задані додаткові умови
, що задово-льняє задані додаткові умови
 (7.3)
(7.3) – сталі.
– сталі. і
і  є оригіналами. Позначивши зображення шуканої функції через
є оригіналами. Позначивши зображення шуканої функції через  , запишемо наступні співвідношення:
, запишемо наступні співвідношення: ,
,  ,
,  .
. розглядається як параметр.
розглядається як параметр.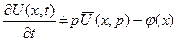 ,
, .
. – оригінал, тоді крайові умови у просторі зображень матимуть вигляд
– оригінал, тоді крайові умови у просторі зображень матимуть вигляд (7.4)
(7.4)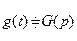 .
.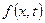 є оригіналом, операційний метод приводить розв’язання поставленої неста-ціонарної задачі (7.2)–(7.3) до розв’язання звичайного дифе-ренціального рівняння другого порядку
є оригіналом, операційний метод приводить розв’язання поставленої неста-ціонарної задачі (7.2)–(7.3) до розв’язання звичайного дифе-ренціального рівняння другого порядку (7.5)
(7.5) ,
,  ,
,  ,
,  і
і 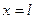 закріплені жорстко. Початкове відхилення задано рівністю
закріплені жорстко. Початкове відхилення задано рівністю 
 , початкова швидкість рівна нулю. Знайти відхилення
, початкова швидкість рівна нулю. Знайти відхилення  .
. Задача зводиться до розв’язання диференційного рівняння
Задача зводиться до розв’язання диференційного рівняння ,
,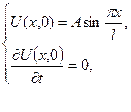 К.У.
К.У. 
 ,
, .
. , (7.6)
, (7.6)
 ,
, – загальний розв’язок відповідного однорідного рівняння
– загальний розв’язок відповідного однорідного рівняння  .
. . Звідси
. Звідси .
. .
.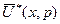 знайдемо у вигляді
знайдемо у вигляді  .
. підставимо частин-ний розв’язок у (7.6) та отримаємо рівняння
підставимо частин-ний розв’язок у (7.6) та отримаємо рівняння .
. .
.
 .
.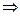

 з врахуванням формули оберненого перетворення
з врахуванням формули оберненого перетворення
 ,
,
 , який задовольняє початковим і граничним умовам
, який задовольняє початковим і граничним умовам  (
( ),
),  .
. Задача зводиться до розв’язання диференційного рівняння
Задача зводиться до розв’язання диференційного рівняння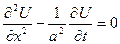 , яке задовольняє задані додаткові умови
, яке задовольняє задані додаткові умови , К.У.
, К.У.  .
. ,
, ,
, ,
, .
. .
. .
. .
. .
. .
. .
. .
.
 ,
, дійсного аргументу
дійсного аргументу 


