
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 7 Елементи операційного численняСодержание книги
Поиск на нашем сайте
Застосування операційного числення при розв’язуванні диференціальних рівнянь з частинними похідними
Ефективним способом розв’язування диференціальних рівнянь з частинними похідними є використання операційних методів, зокрема, перетворення Лапласа. Природно сподівати-ся, що застосування цього методу для розв’язання таких рів-нянь приведе до переведення однієї зі змінних у просторі оригіналів до параметра у просторі зображень. Так, якщо в розглядуваному рівнянні невідомою є функ-ція двох змінних, то застосування операційного методу до однієї зі змінних приведе до звичайного диференціального рівняння зображення відносно другої змінної. Щоб знайти зображення, отримане рівняння можна розв’язувати з використанням теорії диференційних рівнянь або знову застосувати перетворення Лапласа та одержати скінченне зображувальне рівняння щодо другого параметра. Далі застосовуємо обернене перетворення Лапласа один раз у першому випадку та двічі у другому і отримаємо в просторі оригіналів шукану функцію [5].
Відомості про операційне числення Означення 7.1 Оригіналом називається така функція 1) 2) 3) Означення 7.2 Зображенням функції-оригінала
Інтеграл Лапласа (7.1) називають перетворенням Лапласа функції Іноді використовують таке позначення:
Властивості зображень Властивість лінійності Якщо Властивість подібності Якщо
Властивість зміщення Якщо оригінал Властивість запізнення Якщо оригінал Властивість диференціювання оригінала Нехай
Зокрема, якщо
Зокрема, коли
Зауважимо, що ця властивість широко використовується при розв’язуванні лінійних диференціальних рівнянь із сталими коефіцієнтами та їх систем.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.51 (0.007 с.) |

 дійсного аргумента
дійсного аргумента  , яка задовольняє наступні три умови:
, яка задовольняє наступні три умови: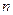 -го порядку при
-го порядку при 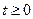 ;
; росте не швидше, ніж деяка показникова функ-ція, тобто існують такі сталі додатні числа
росте не швидше, ніж деяка показникова функ-ція, тобто існують такі сталі додатні числа 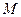 і
і 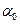 , які не залежать від
, які не залежать від 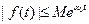 для всіх
для всіх 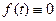 при
при 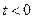 .
.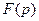 комплексної змінної
комплексної змінної 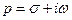 , яка визначається інтегралом Лапласа:
, яка визначається інтегралом Лапласа: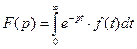 . (7.1)
. (7.1)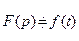 , або
, або 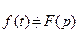 .
.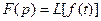 , де символ
, де символ 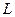 означає перетворення Лапласа.
означає перетворення Лапласа.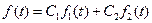 і при цьому,
і при цьому, 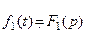 ,
,  , то
, то  .
.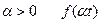 також оригінал і
також оригінал і 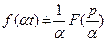 .
. , то для довільної сталої
, то для довільної сталої  має місце відповідність:
має місце відповідність: 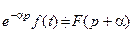
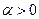 , то
, то 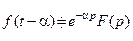 .
.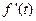 , яка є теж оригіналом, то
, яка є теж оригіналом, то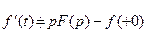 .
. , то диференціювання оригіналу зводиться до множення зображення на
, то диференціювання оригіналу зводиться до множення зображення на  . Якщо оригінал
. Якщо оригінал 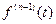 неперервна, то
неперервна, то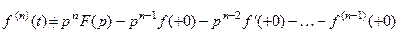
 , то
, то .
.


