
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння Лапласа в циліндричних координатах
Нехай
Введемо у розгляд циліндричні координати
Звідси зворотній зв’язок:
Щоб записати рівняння Лапласа в циліндричних корди-натах, знайдемо відповідні частинні похідні функції
Враховуючи, що:
отримаємо:
Це і є рівняння Лапласа в циліндричних координатах. Якщо функція U не залежить від z, а лише від x та y, то рівняння Лапласа буде мати вигляд
де r та ня є рівнянням Лапласа в полярних координатах. Приклад 6.3 Знайдемо розв’язок рівняння Лапласа в області D, що обмежена двома колами
К.У. де
Розв’язуємо задачу у полярних координатах. Очевидно, шукана функція
Це звичайне диференціальне рівняння другого порядку, яке допускає пониження порядку. Інтегруючи його, знайдемо
Визначимо
звідси остаточно отримаємо:
Задача діріхле для круга
Нехай у площині хоу є круг радіуса R з центром в початку координат. на його колі задана деяка функція
К.У. Припустимо, що
Будемо шукати розв’язок за методом Фур’є, подаючи функцію
Підставляючи її в рівняння та враховуючи, що
Відокремимо змінні:
Отже, рівняння Лапласа розпалося на два диференціаль-них рівняння:
З рівняння (І) маємо
k2+λ=0,
Тоді
Оскільки задана область є кругом, то при збільшенні кута Тоді отримаємо множину функцій:
Коефіцієнти
Розв’язок цього рівняння будемо шукати у вигляді
Поділивши на
Зазначимо, що
Завдяки лінійності та однорідності рівняння Лапласа сума частинних розв’язків:
буде також розв’язком рівняння Лапласа. Для знаходження коефіцієнтів
Це є ряд Фур’є для функції
Звідси:
Таким чином, розв’язком задачі Діріхле у крузі радіуса R є функція (6.52) з коефіцієнтами (6.53). Контрольні запитання 6.1 На яких припущеннях будується виведення рівняння теплопровідності? 6.2 Проаналізувати фізичний зміст величин, що входять у рів- няння теплопровідності. 6.3 У чому полягає постановка задачі нестаціонарної тепло- провідності? 6.4 Особливості застосування методу Фур’є до задач теплопровідності. 6.5 Якими диференціальними рівняннями з частинними похід- ними моделюються стаціонарні процеси? 6.6 Постановка задачі стаціонарної теплопровідності. 6.7 Що характеризує вільний член F(x,t) у рівнянні теплопро- відності 6.8 Які крайові задачі виділяють у залежності від способу за- дання крайової умови? 6.9 Задача Діріхле для рівняння Лапласа. 6.10 задача Неймана. 6.11 Мішана крайова задача. 6.12 Рівняння Лапласа в полярних та циліндричних координатах. 6.13 Застосування методу Фур’є при розв’язуванні задачі Діріхле для круга.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.168.172 (0.022 с.) |
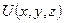 – гармонічна в деякій області
– гармонічна в деякій області  функція трьох змінних. Тоді для неї рівняння Лапласа має вигляд:
функція трьох змінних. Тоді для неї рівняння Лапласа має вигляд: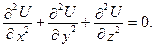 (6.43)
(6.43)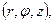 які пов’язані з декартовими координатами формулами
які пов’язані з декартовими координатами формулами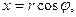
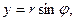
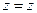 ,
,  (6.44)
(6.44)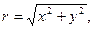
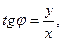
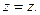 (6.45)
(6.45)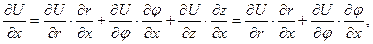
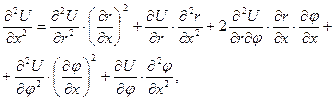
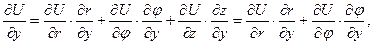
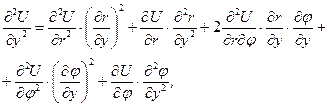
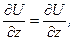
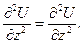
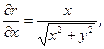
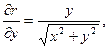
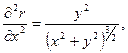

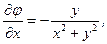
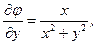
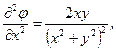
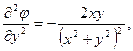
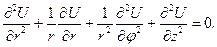 (6.46)
(6.46)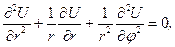 (6.47)
(6.47) – полярні координати на площині. Знайдене рівнян-
– полярні координати на площині. Знайдене рівнян-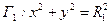 та
та 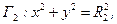 якщо значення шуканої функції на колах:
якщо значення шуканої функції на колах: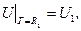
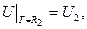
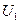 та
та 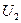 – сталі.
– сталі. Це може бути, наприклад, задача про стаціонарний розподіл температури у кільці між двома колами, якщо на самих колах температура задана.
Це може бути, наприклад, задача про стаціонарний розподіл температури у кільці між двома колами, якщо на самих колах температура задана. не залежить від кута
не залежить від кута 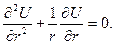
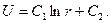
 та
та 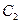 із крайових умов:
із крайових умов: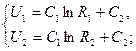
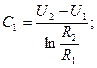



 де
де  неперервну у крузі, яка задовольняє всередині круга рівнянню Лапласа [1]. Постановка задачі в полярних координатах має вигляд:
неперервну у крузі, яка задовольняє всередині круга рівнянню Лапласа [1]. Постановка задачі в полярних координатах має вигляд: ,
,  ,
,
 можна розкласти в ряд Фур’є на
можна розкласти в ряд Фур’є на  . Перепишемо рівняння Лапласа, домноживши його на
. Перепишемо рівняння Лапласа, домноживши його на 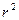 :
:
 у вигляді добутку двох функцій, кожна з яких залежить від однієї змінної:
у вигляді добутку двох функцій, кожна з яких залежить від однієї змінної: (6.48)
(6.48) та
та  отримаємо:
отримаємо:
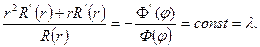
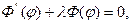 (І)
(І)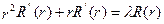 . (ІІ)
. (ІІ)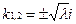 .
.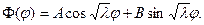 (6.49)
(6.49)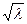 має бути цілим:
має бути цілим: 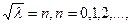 або
або 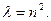
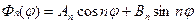 ,
, 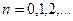
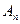 та
та 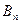 залишились невизначеними. Розглянемо рівняння (ІІ):
залишились невизначеними. Розглянемо рівняння (ІІ):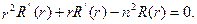
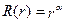 , де
, де  – невідомий параметр. Підставимо цю функ-цію у рівняння:
– невідомий параметр. Підставимо цю функ-цію у рівняння: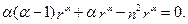 (6.50)
(6.50)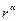 , отримаємо:
, отримаємо: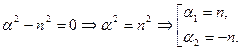
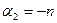 – сторонній корінь, оскільки при
– сторонній корінь, оскільки при 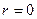 функція
функція 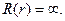 Отже,
Отже, 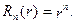 Остаточно маємо:
Остаточно маємо: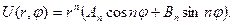 (6.51)
(6.51)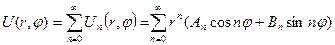 (6.52)
(6.52)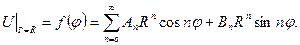
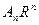 та
та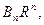 які визначаються за формулами Фур’є:
які визначаються за формулами Фур’є: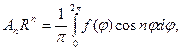
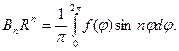
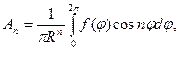
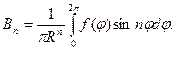 (6.53)
(6.53)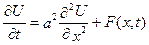 ?
?


