
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Фур’є для розв’язування задачі про поздовжні коливання стержняСодержание книги
Поиск на нашем сайте
Враховуючи, що метод Фур’є застосовують при однорід-них крайових умовах, розглянемо задачу про вільні коливан-ня стержня, один кінець якого (
П.У.
Припустимо, що функції
Після підстановки (5.2) у хвильове рівняння, отримаємо:
Враховуючи попередні дослідження, відразу розглянемо випадок, який приводить до коливального процесу, оскільки в інших випадках отримуємо тільки нульові розв’язки. Нехай
Розглянемо спочатку перше рівняння і знайдемо функцію
Характеристичне рівняння
Отже,
де А та В – довільні сталі, які будемо шукати із крайових умов (5.1):
Тут
Тут
Звідси визначаємо
Тому Тепер розглянемо рівняння (ІІ) і знайдемо функцію
Характеристичне рівняння
Тоді загальний розв’язок з урахуванням того, що
Запишемо частинний розв’язок поставленої задачі:
Враховуючи позначення, запишемо загальний розв’язок як суму всіх частинних:
або в розгорнутому вигляді:
Щоб знайти невідомі коефіцієнти
Тепер запишемо початкові умови
Фактично ми отримали розклади функцій Таким чином, розв’язок задачі про поздовжні коливання стержня, один кінець якого жорстко закріплений, а другий вільний, має вигляд:
де
Приклад 5.1 Розв’язати задачу про поздовжні коливання стержня, один кінець якого жорстко закріплений, а до вільно-го кінця прикладено силу P, причому в момент t =0 дія сили раптово припиняється.
Тобто функції Щоб побудувати розв’язок у вигляді (5.8) знайдемо коефіцієнти
Тоді розв’язок задачі:
Приклад 5.2 Поставити і розв’язати задачу про поздовжні коливання стержня, один кінець якого жорстко закріплено, а до вільного кінця раптово у момент часу
П.У.
Для того, щоб розв’язати задачу з ненульовими крайовими умовами зробимо заміну
Отримаємо початкові і крайові умови для функції
Постановка задачі для функції
П.У. Знайшовши Контрольні запитання 5.1 У чому полягає постановка для розв’язування задачі про поздовжні коливання стержня? 5.2 У чому полягає суть методу Фур’є для розв’язування задач про поздовжні коливання стержня? 5.3 У чому особливість методу Фур’є стосовно вимог до крайових умов?
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.134.18 (0.006 с.) |

 ) жорстко закріплений, а другий (
) жорстко закріплений, а другий (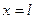 ) вільний. Ця задача має наступну постановку:
) вільний. Ця задача має наступну постановку: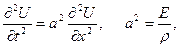
 ,
, К.У.
К.У.  (5.1)
(5.1) та
та  можна розкласти в ряд Фур’є по синусах кратних дуг на
можна розкласти в ряд Фур’є по синусах кратних дуг на  За методом Фур’є ненульові розв’язки хвильового рівняння, які задовольняють однорідні крайові умови (5.1), шукаємо у вигляді
За методом Фур’є ненульові розв’язки хвильового рівняння, які задовольняють однорідні крайові умови (5.1), шукаємо у вигляді 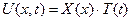 . Знайдемо частинні похідні:
. Знайдемо частинні похідні:
 (5.2)
(5.2) (5.3)
(5.3) . Тоді хвильове рівняння розіб’ється на два одно-рідних диференціальних рівняння другого порядку зі сталими коефіцієнтами відносно функцій
. Тоді хвильове рівняння розіб’ється на два одно-рідних диференціальних рівняння другого порядку зі сталими коефіцієнтами відносно функцій  та
та  .
. (І)
(І) . (ІІ)
. (ІІ) .
.

 (5.4)
(5.4)
 , щоб уникнути тривіального розв’язку задачі. Знайдемо
, щоб уникнути тривіального розв’язку задачі. Знайдемо 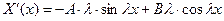 . Тоді крайові умови набувають вигляду:
. Тоді крайові умови набувають вигляду: (5.5)
(5.5) за умовою,
за умовою,  , щоб виключити можливість отримання нульового розв’язку. Тоді
, щоб виключити можливість отримання нульового розв’язку. Тоді 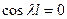 ,
, .
.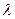 , як множину чисел
, як множину чисел 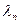 :
: . (5.6)
. (5.6) коефіцієнт
коефіцієнт 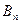 залишився невизначеним.
залишився невизначеним.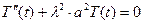 .
.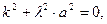

 буде таким:
буде таким: (5.7)
(5.7)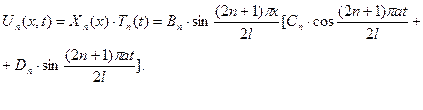 Введемо позначення:
Введемо позначення:  та
та 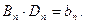
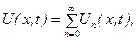 (5.8)
(5.8) (5.9)
(5.9) та
та  , скористаємося початковими умовами. Але спочатку знайдемо
, скористаємося початковими умовами. Але спочатку знайдемо 

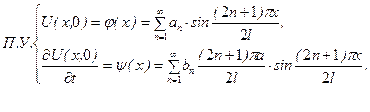 (5.10)
(5.10)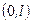 . Тому коефіцієнти розкладів
. Тому коефіцієнти розкладів 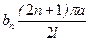 можна визначити за відповідними формулами Фур’є.
можна визначити за відповідними формулами Фур’є.
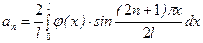 , (5.11)
, (5.11)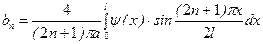 .
. Ця задача має наступну постановку:
Ця задача має наступну постановку:

 ,
,  Звідси
Звідси 
 .
.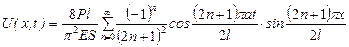 .
. 
 прикладено розтягуючу силу P.
прикладено розтягуючу силу P.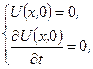 К.У.
К.У. 
 :
: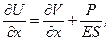
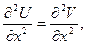
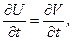
 .
. :
:


 К.У.
К.У. 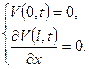
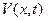 за методом Фур’є, відповідь запишемо у вигляді
за методом Фур’є, відповідь запишемо у вигляді 



