
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зведення до канонічного виду диференціального рівняння другого порядкуСодержание книги
Поиск на нашем сайте
Розглянемо диференціальне рівняння з частинними похідними, яке є лінійним відносно похідних другого поряд-ку:
де A, B, C – сталі (в загальному випадку можуть бути і функціями, визначеними в деякій області D площини xOy з неперервними похідними до другого порядку включно), F – неперервна функція [4]. Л. Ейлер довів, що будь-яке диференціальне рівняння виду (1.1) за допомогою заміни незалежних змінних Поставимо задачу: за допомогою заміни змінних x і y звести рівняння (1.1) до найпростішого (канонічного) виду. Введемо нові змінні
Нехай функції
в області D. Виразимо похідні через нові змінні:
Підставляючи ці похідні в (1.1), отримаємо:
де
Явний вираз
Поділивши (1.4) на
яке фактично розпадається на два:
Криву z(x, y)=const, що є розв’язком рівняння (1.4) будемо називати характеристичною кривою, а саме рівняння (1.4) − рівнянням характеристик. З умови z (x, y)= const випливає, що
z'x dx+ z'y dy = 0.
Звідси маємо простий зв'язок з похідними функції z(x, y)
Ввівши відповідну заміну в (1.5) і (1.6), отримаємо:
Розв'язки рівнянь (1.5) і (1.6) пов'язані з розв'язком рівнянь (1.7) і (1.8) наступним чином. Нехай
− загальні інтеграли рівнянь (1.7) і (1.8). Тоді функції
А(dy)²−2Bdxdy+C(dx)²=0. (1.10)
Очевидно, що розв’язки рівнянь (1.7) і (1.8), а значить канонічний вид рівняння (1.1), залежить від знаку дискримінанта D=В²−АС, або знаку визначника
у всій області У залежності від цього розглянемо три випадки: 1) Нехай у розглядуваній області ∆ < 0 (D = В²−АС >0) − рівняння гіперболічного типу (можна вважати, що або У цьому випадку загальні інтеграли (1.9) визначають дві дійсних і різних сім'ї характеристик. Оскільки функції φ(x, y) і ψ(x, y) задовольняють рівняння (1.4), то, поклавши в (1.2)
отримаємо Розділивши рівняння (1.3) почленно на 2В, одержимо канонічний вид рівняння гіперболічного типу:
При
Це другий канонічний вид рівняння канонічного типу. 2)Нехай ∆=0 (D=В²−АС =0) – рівняння параболічного типу. В силу вказаної умови можна припустити, що в кожній точці розглядуваної області один з коефіцієнтів У цьому випадку загальні інтеграли (1.9) дійсні і співпа-дають. Таким чином, є тільки одна сім'я характеристик. Рівняння (1.5) і (1.6) також співпадають і набувають вигляду
Не важко бачити, що будь-який розв’язок
Врахувавши це, маємо ξ= φ(x, y), аза η(x, y), візьмемо будь-яку двічі неперервнодиференційовну функцію, для якої якобіан
Тоді Поділивши рівняння (1.3) на
Зауважимо, якщо 3) Нехай ∆>0 (D=В²−АС <0) − рівняння еліптичного типу. Тут загальні інтеграли (1.9) є комплексними величинами. Тобто рівняння еліптичного типу не мають дійних характеристик. Нехай φ(x, y)≡ φ1(x, y)+ іφ2(x, y)= С1 − один із загальних інтегралів (1.9); другий загальний інтеграл буде комплексно спряженим з даним. Покладемо в (1.2): ξ= φ1(x, y), η=φ2(x, y). Підставляючи в рівняння (1.4) його розв'язок φ=ξ+іη, отримаємо
Відокремлюючи у цій тотожності дійсну та уявну частини, одержимо:
Звідси випливає, що
Приклад 1.2 Знайти загальний розв’язок рівняння, звівши його до канонічного виду
Запишемо рівняння характеристик
Поділивши на
Знайдемо
Розв’яжемо ці рівняння.
Введемо заміну змінних
Знайдемо всі частинні похідні, що входять у задане рівняння, виразивши їх через
Підставивши
Після спрощень одержуємо Інтегруємо по змінній Інтегруємо обидві частини по
де Приклад 1.3 Знайти загальний розв’язок рівняння, звівши його до канонічного виду
Запишемо рівняння характеристик
Поділивши на
Знайдемо
Звідси Введемо заміну змінних: За другу нову змінну візьмемо, наприклад, Знайдемо всі частинні похідні, що входять у задане рівняння, виразивши їх через
Підставивши Інтегруємо двічі по змінній
де Повертаючись до змінних Приклад 1.4 Звести до канонічного виду рівняння
Запишемо рівняння характеристик
Поділивши на
Знайдемо
Звідси
Введемо заміну змінних:
Тоді Знайдемо всі частинні похідні, що входять у задане рівняння, виразивши їх через
Підставивши
Зауваження: наведена класифікація лінійних рівнянь зі сталими коефіцієнтами переноситься і на рівняння зі змінними коефіцієнтами, які в нашому посібнику не розглядаються.
Контрольні запитання 1.1 Що є предметом математичної фізики? 1.2 За допомогою яких математичних засобів моделюються фізичні задачі та явища, пов’язані з температурними, хвильо- вими та іншими процесами? 1.3 Означення диференціального рівняння з частинними похідними, його порядок. 1.4 Що є розв’язком диференціального рівняння з частинними похідними і від чого він залежить? 1.5 Чим відрізняється загальний розв’язок диференціального рівняння з частинними похідними від загального розв’язку диференціального рівняння? 1.6 Які фізичні процеси та явища описуються канонічними ди- ференціальними рівняннями гіперболічного (еліптичного, па- раболіного) типу? 1.7 Як звести диференціальне рівняння з частинними похідни- ми, яке є лінійним відносно похідних другого порядку, до ка- нонічного типу? 1.8 Мета зведення диференціального рівняння з частинними похідними до канонічного типу. 1.9 Класифікація диференціального рівняння з частинними похідними другого порядку. 1.10 Як канонічний вид диференціального рівняння другого порядку з частинними похідними залежить від знаку визнач- ника
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.166 (0.007 с.) |

 (1.1)
(1.1) і
і  можна привести до одного з трьох видів (типів), відомих як гіперболічний, параболічний та еліптичний (по аналогії з теорією кривих другого порядку в курсі аналітичної геометрії) [1].
можна привести до одного з трьох видів (типів), відомих як гіперболічний, параболічний та еліптичний (по аналогії з теорією кривих другого порядку в курсі аналітичної геометрії) [1]. (1.2)
(1.2) і
і  – двічі неперервно-диференційовані і якобіан
– двічі неперервно-диференційовані і якобіан
 ,
,  ;
;


 (1.3)
(1.3)


 нас не цікавить. Спробуємо вибрати функції
нас не цікавить. Спробуємо вибрати функції  ,
,  ,
,  стали рівними нулю. Очевидно, щоб вирішити питання про рівність нулю коефіцієнтів
стали рівними нулю. Очевидно, щоб вирішити питання про рівність нулю коефіцієнтів  (1.4)
(1.4) отримаємо квадратне рівняння відносно
отримаємо квадратне рівняння відносно 

 (1.5)
(1.5) (1.6)
(1.6)
 (1.7)
(1.7) (1.8)
(1.8)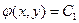 ,
,  (1.9)
(1.9) і
і  будуть розв'язками рівнянь (1.5) і (1.6) відповідно, а значить і розв'язками рівняння (1.4). Криві (1.9) називаються характеристиками рівняння (1.1). Зазначимо, що рівняння (1.7) і (1.8) у загальнішій формі можна подати у вигляді одного характеристичного рівняння:
будуть розв'язками рівнянь (1.5) і (1.6) відповідно, а значить і розв'язками рівняння (1.4). Криві (1.9) називаються характеристиками рівняння (1.1). Зазначимо, що рівняння (1.7) і (1.8) у загальнішій формі можна подати у вигляді одного характеристичного рівняння:
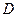 .
. , або
, або  ).
). ,
,  , (1.11)
, (1.11)
 (оскільки знак дискримінанта не змінюється при заміні змінних).
(оскільки знак дискримінанта не змінюється при заміні змінних). .
. рівняння (1.1) належить гіперболічному типу і вже має канонічний вид. Якщо рівняння (1.1) було лінійним відносно похідних першого порядку і самої функції
рівняння (1.1) належить гіперболічному типу і вже має канонічний вид. Якщо рівняння (1.1) було лінійним відносно похідних першого порядку і самої функції  , то після перетворення рівняння також буде лінійним. Якщо в цьому рівнянні покласти
, то після перетворення рівняння також буде лінійним. Якщо в цьому рівнянні покласти  ,
,  , то рівняння набуде вигляду:
, то рівняння набуде вигляду: .
. ,
,  відмінний від нуля. Нехай
відмінний від нуля. Нехай  .
.

 цього рівняння в силу
цього рівняння в силу  задовольняє також рівняння:
задовольняє також рівняння:

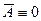 . Враховуючи, що D = 0(а це означає що і
. Враховуючи, що D = 0(а це означає що і  ), отримаємо, що
), отримаємо, що  , а коефіцієнт
, а коефіцієнт  набуває виду
набуває виду 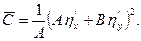
 одержимо канонічне рівняння параболічного типу:
одержимо канонічне рівняння параболічного типу: .
. , а
, а  зліва.
зліва.
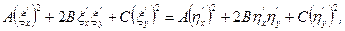


 . Тоді отримаємо рівняння еліптичного виду:
. Тоді отримаємо рівняння еліптичного виду:
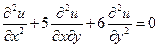 .
. Тут
Тут  . Отже, задане рівняння гіперболічного типу.
. Отже, задане рівняння гіперболічного типу. .
. , отримаємо
, отримаємо .
. .
.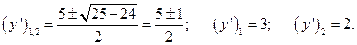
 ,
, .
. або
або 
 :
:





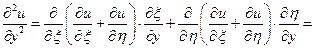

 у задане рівняння, отримає-мо
у задане рівняння, отримає-мо
 .
. .
.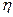 (можна по
(можна по  ). Тоді
). Тоді  , де
, де  – довільна функція змінної
– довільна функція змінної 
 і
і  – довільні двічі диференційовні в розглядуваній області функції. Повертаючись до змінних
– довільні двічі диференційовні в розглядуваній області функції. Повертаючись до змінних  отримаємо
отримаємо  Це і буде загальним розв’язком заданого рівняння.
Це і буде загальним розв’язком заданого рівняння. 
 .
.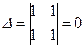 . Отже, задане рівняння параболічного типу.
. Отже, задане рівняння параболічного типу. .
. .
. .
. .
.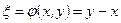 .
. (очевидно, що
(очевидно, що  незалежні).
незалежні). ;
; ;
;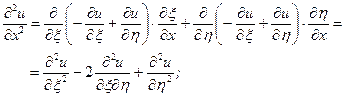
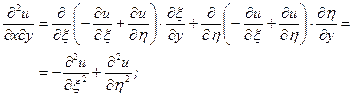
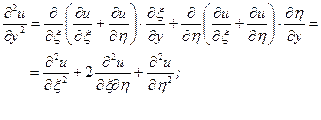
 .
. ,
,  ,
,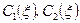 – довільні функції змінної
– довільні функції змінної  . Це і буде загальним розв’язком заданого рівняння.
. Це і буде загальним розв’язком заданого рівняння.  .
.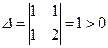 . Отже, задане рівняння еліптичного типу.
. Отже, задане рівняння еліптичного типу. .
. .
. .
.

 – один із загальних інтегралів, другий буде спряженим до нього;
– один із загальних інтегралів, другий буде спряженим до нього; ,
,  .
. ;
;

 .
. 


