Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Фур’є для розв’язування задачі теплопровідностіСодержание книги
Поиск на нашем сайте
Розглянемо задачу теплопровідності у скінченному стержні довжиною l. нехай його кінці відповідають точкам х=0 та х=l на осі Ох. Враховуючи специфіку метода Фур’є, розглянемо ряд задач з однорідними крайовими умовами. 1) Знайти розподіл температур в стержні, на кінцях якого весь час підтримується нульова температура, а початковий розподіл задається функцією Поставимо задачу:
П.У. Для неперервності U(х; t) в точках (0; 0) і (l; 0 ) необхідно вимагати, щоб φ (0) =φ (l) =0. Також припускаємо, що функцію
Підставляючи цю функцію у рівняння теплопровідності, отримаємо:
або
Останній факт було досліджено при розв’язуванні задач про коливання. Таким чином, рівняння теплопровідності розпадається на два звичайних диференціальних рівняння:
Розглянемо спочатку перше рівняння і знайдемо функцію Для знаходження невідомих сталих, використовуємо крайові умови, записані для функції К.У. Звідси: Очевидно, що
Отже, маємо:
Тепер з рівняння (ІІ) знайдемо функцію
Враховуючи, що
Таким чином, знайдено частинні розв’язки рівняння тепло- провідності:
Оскільки рівняння теплопровідності є лінійним та однорідним, то його загальний розв’язок можна знайти, як суму частинних розв’язків:
або, позначивши
Для визначення коефіцієнта
П.У. Звідси:
Для функції
Таким чином, розв’язок задачі про поширення тепла у стержні, на кінцях якого підтримується нульова температура, а початковий розподіл температур задається функцією Зауваження Розглянемо випадок, коли на кінцях стержня задається ненульова температура. Тоді задача має наступну постановку:
П.У.
Тут У цій задачі з неоднорідними граничними умовами достатньо зробити підстановку:
яка зведе її до попередньої задачі відносно функції Розглянемо ще одну задачу про поширення тепла у стержні. 2) Знайти розподіл температур в стержні, на одному кінці якого весь час підтримується нульова температура, а другий кінець теплоізольвано при довільній початковій умові. Поставимо задачу:
П.У. U(x,0)=φ(x), К.У.
Зазначимо, що тут не суттєво, який кінець теплоізольовано. Як бачимо, крайові умови однорідні. Розв’яжемо цю задачу за методом Фур’є, згідно якого
Тоді рівняння теплопровідності:
або
Розглянемо рівняння
розв’язок якого Сталі А та В шукаємо із крайових умов:
К.У.
Розпишемо граничні умови:
Очевидно, що Звідси Отже,
Розв’яжемо друге рівняння для функції
Розв’язок цього рівняння:
Враховуючи, що
Отже, маємо
Поклавши
Коефіцієнти
Отже, формули (6.30) і (6.31) дають розв’язок даної задачі. 3) Розв’язати задачу про поширення тепла в стержні, на одному кінці якого стала температура U0, а другий – теплоізольований. Поставимо задачу:
П.У. U(x,0)=φ(x), К.У. За методом Фур’є крайові умови мають бути нульовими. Тому проведемо заміну
Рівняння теплопровідності:
К.У.
П.У.
За методом Фур’є отримаємо
де
Отже, остаточно маємо: Приклад 6.2 Розв’язати задачу про поширення тепла у стержні довжиною l, на кінцях якого весь час підтримується нульова температура, а початковий розподіл температур задається функцією
П.У.
Згідно з методом Фур’є ця задача має розв’язок:
де Як відомо, система власних функцій
Таким чином, усі коефіцієнти
Тоді розв’язок задачі запишемо так
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.68.196 (0.01 с.) |




 ,
, К.У.
К.У.  (6.19)
(6.19) можна розкласти по синусах кратних дуг на проміжку
можна розкласти по синусах кратних дуг на проміжку  . Згідно методу Фур’є ненульові розв’язки рівняння, що задовольняють умови (6.19), шукаємо у вигляді добутку двох функцій:
. Згідно методу Фур’є ненульові розв’язки рівняння, що задовольняють умови (6.19), шукаємо у вигляді добутку двох функцій:


 , (І)
, (І) (ІІ)
(ІІ)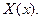 Оскільки розв’язки характеристичного рівняння є комплексно спряженими
Оскільки розв’язки характеристичного рівняння є комплексно спряженими 
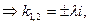 то шукана функція набуває вигляду
то шукана функція набуває вигляду 



 (інакше отримаємо тривіальний роз-в’язок). Тоді:
(інакше отримаємо тривіальний роз-в’язок). Тоді:
 ,
,  (6.20)
(6.20) Це дифере-нціальне рівняння першого порядку з відокремлюваними змінними:
Це дифере-нціальне рівняння першого порядку з відокремлюваними змінними:
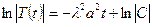 , тоді
, тоді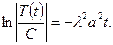
 , остаточно маємо:
, остаточно маємо: ,
,  (6.21)
(6.21)

 , запишемо:
, запишемо: (6.22)
(6.22)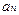 скористаємося початко-вою умовою:
скористаємося початко-вою умовою:
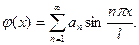
 отримано розклад в ряд Фур’є за сину-сами в інтервалі
отримано розклад в ряд Фур’є за сину-сами в інтервалі 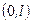 з коефіцієнтами розкладу
з коефіцієнтами розкладу  (6.23)
(6.23) шукається за формулами (6.22), (6.23).
шукається за формулами (6.22), (6.23).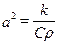 ,
,  К.У.
К.У. 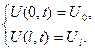 (6.24)
(6.24) та
та  – сталі температури відповідно на кінцях х= 0 та x=l.
– сталі температури відповідно на кінцях х= 0 та x=l.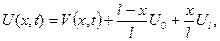 (6.25)
(6.25) Цю процедуру пропонується виконати студентам самостійно.
Цю процедуру пропонується виконати студентам самостійно.
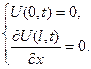 (6.26)
(6.26)
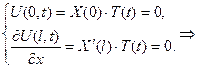


 тоді
тоді 
 ,
, 
 . (6.28)
. (6.28) , що одержується з рівняння теплопровідності:
, що одержується з рівняння теплопровідності: .
.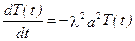
 .
. .
.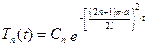 . (6.29)
. (6.29)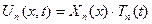 і розв’язок даної зада-чі шукаємо у вигляді:
і розв’язок даної зада-чі шукаємо у вигляді:
 . (6.30)
. (6.30) (6.31)
(6.31) (6.32)
(6.32)


 (6.33)
(6.33)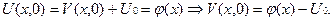
 (6.34)
(6.34)

 Поставимо задачу:
Поставимо задачу: К.У.
К.У. 


 є ортогональною на проміжку
є ортогональною на проміжку 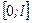 , тобто
, тобто коли
коли  , і не дорівнює нулю, коли
, і не дорівнює нулю, коли  .
.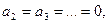 проте коефіцієнт
проте коефіцієнт 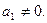 Знайдемо його:
Знайдемо його: