
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стаціонарні процеси. Рівняння Лапласа
Стаціонарні процеси моделюються диференціальними рівняннями з частинними похідними еліптичного типу. Це процеси різної фізичної природи: коливання (механічні, зву-кові, електромагнітні); теплопровідність, дифузія тощо. Найпростішим рівнянням такого типу є рівняння
яке називається рівнянням Пуассона. Функція Відповідне однорідне рівняння
називається рівнянням Лапласа. Наприклад, таким рівнянням описується стаціонарний розподіл температури у тривимірному тілі. Дійсно, якщо температура Зауважимо, що у двовимірному випадку рівняння Лапласа (6.36) набуває вигляду: Функцію У кожній задачі математичної фізики, пов’язаній з рівнянням Лапласа, шуканий розв’язок виділяється із множи-ни усіх гармонічних функцій за допомогою додаткової умови, якою є крайова умова. Завдяки стаціонарності процесу початкова умова у цих задачах відсутня. Залежно від способу задання крайової умови виділяють три крайові задачі: задачу Діріхле (першу крайову задачу), за-дачу Неймана (другу крайову задачу) та мішану (третю крайову задачу).
Задача Діріхле
Ця задача (перша крайова задача) у просторі формулюється так: знайти функцію
К.У.
Очевидним можна вважати той факт, що задача Діріхле завжди має розв’язок. Дійсно, якщо, наприклад, кожна точка на поверхні тіла постійно підтримується при певній заданій температурі (яка може бути різною у різних точках поверхні), то у кожній точці тіла встановиться своя температура, яка і дає розв’язок задачі Діріхле при заданих крайових умовах. Також очевидно, що цей розв’язок буде єдиним. Аналогічно формулюється задача Діріхле у двовимірному випадку: знайти функцію
К.У.
Зазначимо, що задача Діріхле розв’язується дуже просто в одновимірному випадку, коли розглядається, наприклад, стаціонарний розподіл температури у тонкому стержні довжи-ни l з теплоізольованою бічною поверхнею. Тоді задача Діріхле ставиться так: знайти функцію
К.У.
Задача Діріхле у цьому випадку має розв’язок
Задача Неймана
задача Неймана (друга крайова задача)формулюється так: знайти функцію К.У. Нагадуємо, що похідна Мішана задача Мішана задача (третя крайова задача) формулюється так: знайти функцію
К.У. де функції ють задачею з косою похідною.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.208.72 (0.008 с.) |
 (6.35)
(6.35)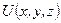 двічі диференційовна, а функція
двічі диференційовна, а функція 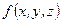 – задана в деякій просторовій області
– задана в деякій просторовій області  .
.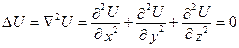 (6.36)
(6.36)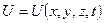 не залежить від часу t, то
не залежить від часу t, то 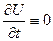 і рівняння теплопровідності зводиться до рівняння Лапласа.
і рівняння теплопровідності зводиться до рівняння Лапласа.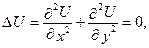 а в одновимір-ному:
а в одновимір-ному: 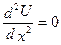 .
. називають гармонічною в області
називають гармонічною в області 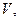 якщо вона неперервна у ній разом зі своїми похідними першого та другого порядків і задовольняє рівняння Лапласа.
якщо вона неперервна у ній разом зі своїми похідними першого та другого порядків і задовольняє рівняння Лапласа.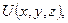 яка задовольняє всередині замкненої поверхні
яка задовольняє всередині замкненої поверхні 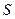 рів-няння Лапласа
рів-няння Лапласа  та набуває у кожній точці М поверхні
та набуває у кожній точці М поверхні 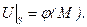 (6.37)
(6.37) яка задовольняє всередині замкненої кривої Г рівняння Лапласа
яка задовольняє всередині замкненої кривої Г рівняння Лапласа  та набуває у кожній точці М кривої Г заданих значенень:
та набуває у кожній точці М кривої Г заданих значенень: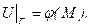 (6.38)
(6.38) яка задовольняє рівняння Лапласа для усіх
яка задовольняє рівняння Лапласа для усіх 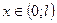 і набуває на кінцях стержня заданих значенень:
і набуває на кінцях стержня заданих значенень: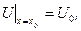
 (6.39)
(6.39) (6.40)
(6.40)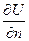 у кожній точці М поверхні
у кожній точці М поверхні 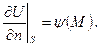 (6.41)
(6.41) яка задовольняє всередині замкненої поверхні
яка задовольняє всередині замкненої поверхні 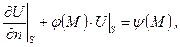 (6.42)
(6.42) та
та 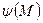 є заданими. Цю задачу ще назива-
є заданими. Цю задачу ще назива-


