
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачі теплопровідностіСодержание книги
Поиск на нашем сайте
Із фізичних міркувань випливає, що для однозначного визначення температури в стержні довжиною Початкова умова для рівняння теплопровідності задає розподіл температур у всіх точках стержня в деякий момент часу, який приймаємо за початковий
П.У. U(x,0)=u|t=0 = φ (х), (6.10)
де φ(х) – задана функція для всіх Крайові умови мають виконуватись там, де стержень може мати теплообмін з навколишнім середовищем, тобто на торцях стержня. Нехай стержень лежить на осі Ох і один його кінець збігається з початком координат ( Крайові умови відображають тепловий режим на кінцях стержня і можуть задаватися по-різному. Розглянемо деякі з них. Нехай на кінцях стержня підтримується стала температура – К.У.
де Запишемо загальніші граничні умови. використовуючи закон Ньютона, запишемо тепловий потік Р, що проходить через одиницю площі за одиницю часу пропорційно зміні температури на торці стержня:
де h – коефіцієнт зовнішньої теплопровідності або коефіцієнт теплообміну, При цьому потік вважається додатним, якщо
Оскільки вектор нормалі паралельний до осі Ох, то для правого кінця потік буде:
a на лівому:
Тепер запишемо умови на лівому і правому кінцях стержня: Г.У. Тут Розглянемо окремі випадки: 1) Нехай коефіцієнт теплообміну К.У. означає, що кінець стержня теплоізольований. 2) Нехай значення коефіцієнт теплообміну
і, переходячи до границі при
К.У.
що означає вільний теплообмін з навколишнім середовищем на кінці х=0. Фактично, це те саме, що розглядалося в першому типі крайових умов. 3) На кінці стержня, не уточнюючи на якому, задається потік, як функція часу
 Приклад 6.1 Поставити задачу про розповсюдження тепла в стержні, один кінець якого теплоізо-льваний, а на другому підтримується стала тем-пература T, причому в момент часу t= 0 розподіл температур у стержні мав вигляд частини параболи з вершиною в початку координат, як зображено на рисунку 6.1. Приклад 6.1 Поставити задачу про розповсюдження тепла в стержні, один кінець якого теплоізо-льваний, а на другому підтримується стала тем-пература T, причому в момент часу t= 0 розподіл температур у стержні мав вигляд частини параболи з вершиною в початку координат, як зображено на рисунку 6.1.
Постановка задачі включає в себе написання рівняння теплопровідності, початкової та граничних умов
П.У.
Розв’язком цієї задачі є функція
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.118.7 (0.006 с.) |

 , крім рівняння теплопровідності, необхідно задати додаткові три умови, які складаються з однієї початкової і двох крайових.
, крім рівняння теплопровідності, необхідно задати додаткові три умови, які складаються з однієї початкової і двох крайових. . Початковий розподіл температур має вигляд:
. Початковий розподіл температур має вигляд: .
. ), а другий має абсцису
), а другий має абсцису 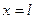 .
. на кінці
на кінці  на кінці
на кінці  (6.11)
(6.11)
 – задані числа (можуть бути і нулі).
– задані числа (можуть бути і нулі).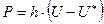 , (6.12)
, (6.12) – температура на кінці стержня,
– температура на кінці стержня, 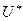 – температура навколишнього середовища поблизу цього кінця.
– температура навколишнього середовища поблизу цього кінця.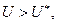 тобто іде процес охолодження стержня. Отже, функція
тобто іде процес охолодження стержня. Отже, функція  (6.13)
(6.13)

 . (6.14)
. (6.14) ,
,  – задані температури навколишнього середовища поблизу відповідних кінців. Оскільки кінці стержня можуть знаходитися в різних середовищах, то сталі
– задані температури навколишнього середовища поблизу відповідних кінців. Оскільки кінці стержня можуть знаходитися в різних середовищах, то сталі 
 взято різними.
взято різними. , тоді крайова умова
, тоді крайова умова (6.15)
(6.15)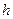 дуже вели-ке. Тоді, наприклад, для лівого кінця маємо:
дуже вели-ке. Тоді, наприклад, для лівого кінця маємо: , (6.16)
, (6.16) , отримаємо крайову умову
, отримаємо крайову умову (6.17)
(6.17) (6.18)
(6.18) Опишемо графік аналітично:
Опишемо графік аналітично: 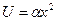 . визначаємо коефіцієнт
. визначаємо коефіцієнт  з того, що точка (l, T) задовольняє рівняння параболи. Отже,
з того, що точка (l, T) задовольняє рівняння параболи. Отже, 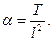 Тоді рівняння параболи має вигляд
Тоді рівняння параболи має вигляд 

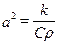 ,
,  ,
, К.У.
К.У. 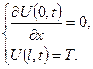
 , яка задовольняє в указаній області рівняння теплопровідності, а також початкову і крайові умови.
, яка задовольняє в указаній області рівняння теплопровідності, а також початкову і крайові умови. 



