
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели надежности восстанавливаемых элементов (объектов, систем)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для оценки надежности восстанавливаемых, т.е. ремонтопригодных элементов (объектов, систем), используются следующие показатели надежности.
1. Вероятность восстановления (функция распределения времени восстановления – Fв)S(t) - вероятность того, что отказавшее изделие будет восстановлено в течение заданного времени ”t”, т.е. вероятность своевременного завершения ремонта. Очевидно, что 0£S(t)£1, S(0)=0, S(¥)=1. Для определения величины S(t) используется следующая статистическая оценка:
где NОВ - число изделий, поставленных на восстановление; NВ - число изделий, время восстановления которых было меньше заданного времени ”t”.
2. Вероятность несвоевременного завершения ремонта (невосстановления) G(t) - вероятность того, что отказавшее изделие не будет восстановлено в течение заданного времени t. Статистическая оценка величины G(t):
Из анализа выражений (3.50) и (3.51) следует, что:
S(t) + G(t) = 1. (3.52)
3. Частота восстановления,
Статистическая оценка величины
где NOB - число изделий, поставленных на восстановление; nВ(Dt) - число восстановленных элементов на интервале времени (
4. Интенсивность восстановления m(t) - условная плотность распределения времени восстановления для момента времени ”t” при условии, что до этого момента восстановление изделия не произошло:
Статистическая оценка величины m(t):
где NB.CP. - среднее число изделий, которые не были восстановлены в интервале времени (0, t). nВ (Dt) - число восстановленных изделий за интервал t.
В отличие от процесса отказов, развивающихся во времени естественным образом, процесс восстановления является целиком искусственным и полностью определяется организационно-технической деятельностью эксплуатационно-ремонтного персонала.
Поэтому кривая интенсивности восстановления, аналогичная кривой интенсивности отказов отсутствует. Так как существуют нормативы времени на проведение ремонтных работ, то m(t) = m = const и численные значения интенсивности восстановления сведены в справочные таблицы по видам оборудования и ремонтов. При постоянстве во времени величины «m» получаем экспоненциальное распределение для времени восстановления:
5. Среднее время восстановления (ТВ) представляет собой математическое ожидание времени восстановления:
Статистическая оценка времени восстановления находится из выражения:
где tвi - время восстановления i-го элемента; NOB – количество изделий, поставленных на восстановление.
При m = const имеем:
Среднее время восстановления включает продолжительность послеаварийного ремонта ТАВ и продолжительность планового ремонта ТПЛ:
ТВ = ТАВ + ТПЛ. (3.61)
Статистическая оценка этой величины определяется из выражения:
где m - количество отказов; ti – время восстановления одного отказа.
Время восстановления - среднее время вынужденного простоя, необходимое для отыскания и устранения одного отказа.
Время восстановления как правило подчиняется не экспоненциальному закону - чаще это нормальное распределение, распределение Вейбулла или Пуассона. Анализ систем с неэкспоненциальным распределением чрезвычайно сложен и практически его расчетная формула не поддается формализации.
В то же время замена реального закона распределения экспоненциальным с тем же математическим ожиданием мало искажает конечные результаты. Поэтому во многих случаях эта замена обоснована. При этом:
где
m - интенсивность восстановления, m(t) = m = const.
Вероятность восстановления:
Среднее время восстановления:
Величина - средняя наработка на отказ.
Параметр потока отказов восстанавливаемого элемента - w(t) - среднее количество отказов элемента в единицу времени, удельная повреждаемость элемента.
По данным эксплуатации из статистической модели имеем:
где
N0 - число элементов на испытании, при условии замены отказавших элементов.
Среднее время наработки на отказ:
Если w(t) - последовательность случайных моментов отказа восстанавливаемой системы, образует поток отказов, то временная последовательность состояний объекта (износ, отказ, восстановление, работа и т.д.) образуют переменный (алтернирующий) процесс восстановления. Если длительность состояний описывается экспоненциальным законом распределения, то процесс считается простейшим пуассоновским. Для него характерны свойства стационарности, ординарности и отсутствия последействия.
а) Поток отказав - стационарный, если вероятность появления того или иного числа отказов на заданном отрезке времени зависит только от его длины и не зависит от того, где он находится.
б) Поток отказов - ординарный, если вероятность появления двух и более отказов на малом отрезке времени - пренебрежимо мала по сравнению с появлением одного отказа.
в) Поток отказов - поток без последействия, если вероятность появления числа отказов на некотором отрезке времени не зависит от числа и характера отказов, возникших до этого отрезка времени.
Таким образом w(t) - последовательность отказов элемента во времени, характеризуемая параметром потока отказов - «w», который является аналогом «l».
Для ординарных потоков эти понятия совпадают, но «w» и «l» имеют разную природу. Поток отказов (w) - безусловная вероятность отказа элемента за единицу времени. Интенсивность отказов (l) - условная вероятность отказа элемента за единицу времени, при условии, что он проработал до момента «t». На рис 3.4 представлена графическая зависимость потока отказов в функции времени.
нормальной работы, что говорит о том, что отказы системы возникают примерно через одинаковые промежутки времени,
0 t1 t2 t3 t Рис 3.4 На рис 3.4 имеем интервал времени интервал времени интервал времени
Вероятность возникновения «m» отказов за время «t» при частоте отказов «w» в пуассоновском потоке событий (отказ, восстановление, т.е. ординарном, стационарном, без последействия) вычисляются по формуле:
При длительности периода работы элемента ЭС t=1 году. или
где m – число восстановлений (число отказов) в рассматриваемом интервале времени.
(3.70)
- это вероятность того, что за год не будет ни одного отказа элемента.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 693; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.01 с.) |

 , (3.50)
, (3.50) , (3.51)
, (3.51) - плотность распределения времени восстановления - определяется по формуле:
- плотность распределения времени восстановления - определяется по формуле: (3.53)
(3.53) , (3.54)
, (3.54)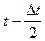 ,
, 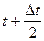 ).
). , (3.55)
, (3.55)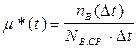 , (3.56)
, (3.56)
 ,
,  (3.57)
(3.57)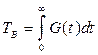 ;
; 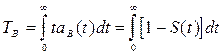 ; (3.58)
; (3.58) ; (3.59)
; (3.59) . (3.60)
. (3.60) , (3.62)
, (3.62)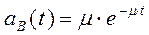 , (3.63)
, (3.63)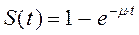 . (3.64)
. (3.64) . (3.65)
. (3.65) 6. Поток отказов w(t) - математическое ожидание числа отказов элементов, происшедшее за единицу времени, при условии, что отказавшие элементы заменяются новыми, т.е. число испытываемых элементов сохраняется одинаковым в процессе эксплуатации.
6. Поток отказов w(t) - математическое ожидание числа отказов элементов, происшедшее за единицу времени, при условии, что отказавшие элементы заменяются новыми, т.е. число испытываемых элементов сохраняется одинаковым в процессе эксплуатации. , (3.66)
, (3.66) , n1(Dt) - количество элементов, отказавших за интервал времени Dt или
, n1(Dt) - количество элементов, отказавших за интервал времени Dt или  ;
; . (3.67)
. (3.67) w(t) Из рис 3.4 видно, что:
w(t) Из рис 3.4 видно, что:  в период
в период равные ее наработке на отказ (рис3.4).
равные ее наработке на отказ (рис3.4). - приработочные дефекты изготовления и монтажа элемента ЭС, например, для ЛЭП это время составляет 1-3 года;
- приработочные дефекты изготовления и монтажа элемента ЭС, например, для ЛЭП это время составляет 1-3 года; - нормальная работа элемента ЭС;
- нормальная работа элемента ЭС;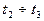 - износ изделия.
- износ изделия.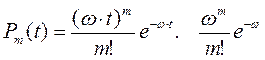 . (3.68)
. (3.68) (3.69)
(3.69) Вероятность безотказной работы элемента:
Вероятность безотказной работы элемента:


