
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Надёжность ЛЭП с последовательно соединёнными элементами.Содержание книги
Поиск на нашем сайте
Предполагая, что отказы ЛЭП и электрических сетей – независимы получим основные формулы для расчёта надёжности комбинации двух элементов. 1. Если р1 – надёжность одного элемента, р2-другого, то вероятность того, что оба будут работать безотказно в течении времени “t”:
где l1, l2-интенсивности отказов элементов, которые м.б. постоянными или переменными во времени; р1, р2 – вероятность отказов элементов ЛЭП. 2. Вероятность того, что один или оба элемента откажут: qпосл(t)=q1(t)+q2(t)-q1(t)+q2(t)=1-P1(t)+1-P2(t)-[1-P1(t)][1-P2(t)]= =1-P1(t)P2(t)=1-Pпосл(t), (4.31) где q1, q2 – вероятность отказов элементов ЛЭП. 3. Вероятность того, что будут работать один или два элемента:
4.Вероятность, что откажут оба элемента ЛЭП:
qпарал(t)=q1(t)q2(t)=[1-р1(t)][1-р2(t)]=1-р1(t)-р2(t)+р1(t)р2(t)=1-рпарал(t) (4.33) Случаи 1 и 2 – представляют противоположные события т.е. рпосл+qпосл=1, поскольку противоположные события для безотказной работы двух элементов осуществляется тремя путями: отказывает один из элементов, либо оба вместе. Следовательно, величины «рпосл» и «qпосл» можно соответственно назвать надёжностью и ненадёжностью последовательного соединения элементов или последовательной системы.Это означает, что отказ любого элемента, приводит к отказу системы.Случаи 3 и 4 –противоположные события т.е. рпарал+qпарал=1, т.к. противоположные события для двух отказавших систем – события, когда один или оба элемента работают безотказно. Величины «рпарал» и «qпарал» называются соответственно надёжностью и ненадёжностью параллельного соединения элементов или системы с постоянным резервом.Это означает, что если один элемент отказал, то существует другой элемент, который выполняет требуемую функцию.Параллельная система из двух элементов не отказывает при отказе одного элемента, если оставшийся удовлетворительно выполняет требуемую функцию. Приведённые формулы используются при экспоненциальном и неэкспоненциальном распределении отказов элементов.В первом случае они упрощаются
ЛЭП и электрические сети обычно состоят из большого числа соединённых последовательно элементов или блоков.В некоторых случаях к заведомо малонадёжным элементам ЛЭП для повышения надёжности подключаются резервные элементы, иногда к целым группам элементов подключаются такие или же подобные группы, включаемые параллельно (например групповое включения вентилей на п/ст ЛЭП постоянного тока).Такие параллельные соединения можно рассматривать как блоки, соединённые последовательно.Система отказывает, если отказывает такой блок в целом. Для «n» элементов или блоков, соединённых последовательно, надёжность системы выражается формулой:
Выражение (4.38) представляет закон произведения надёжности, где рi-надёжность i- го элемента или блока в последовательном соединении.
Надёжность ЛЭП с параллельно соединёнными элементами. Если имеется структурная схема надёжности с последовательным соединением элементов, когда отказ 1-го элемента вызывает отказ 2-го, затем 3-го и т.д., то имеем схему с последовательным соединением зависимых элементов (рис 4.3)
Рис 4.3 В этом случае, если «А» - событие заключающееся в том, что система работает безотказно, а «Аi»(i=1,2….n) – события состоящие в исправной работе элементов системы, то событие «А» имеет место, если имеют место события «Аi». Надёжность системы:
Однако на практике отказ любого элемента – отказ системы. Вероятность безотказной работы, в этом случае, произведение вероятностей для независимых событий:
Так как произведение величин «q» есть намного меньше от сумм этих величин для отдельных элементов
В упрощённых расчётах, для схемы с последовательным соединением элементов, можно принять:
Ошибка при этом упрощении не превышает несколько процентов. Коэффициент отказа (аварийности) «q» обычно для ЛЭП имеет величину: q £ 0.01.
4.4. Надёжность ЛЭП с параллельным соединением элементов . Для определения оптимальной надёжности ЛЭП и электрических сетей на стадии их проектирования приходится иногда дублировать отдельные элементы или цепи – использовать резервирование.На практике используют нагруженный (постоянно включённый) и не нагруженный (холодный) резервы. В последнем случае, когда работает элемент (цепь) имеется один или более резервных элементов (цепей), которые могут вступать в действия при отказе основного рассмотрим надёжность ЛЭП при нагруженном резерве. Имеем для 2-х элементов: вероятность того, что будут работать один или два элемента:
Вероятность, что откажут 2-а элемента:
qпарал(t)=q1(t)q2(t)=[1-p1(t)][1-p2(t)]=1-p1(t)-p2(t)+p1(t)p2(t)=1-pпарал(t). (4.44)
Формулы (4.43) и (4.44) – представлены в пункте 4.3 предыдущей темы. В экспоненциальном случае:
Обобщим эти формулы для общего случая: Сформулируем правило для вычисления вероятности того, что из трёх событий А, В, С, имеющих вероятности P(А), Р(В), Р(С) выполняются либо А, либо В, либо С, либо любая комбинация этих трёх событий.Это правило запишется в виде:
P(A+B+C)=P(A)+P(B)+P(C)-P(A)P(B)-P(A)P(C)-P(B)P(C)+P(A)P(B)P(C). (4.47)
Если события имеют одинаковую вероятность:
P(A)=P(B)=P(C)=P, (4.48)
то
P(A+B+C)=3P-3P2+P3. (4.49)
Аналогично можно иметь формулы для четырёх и более событий. Используя выражение (4.47) можно определить надёжность для трёх параллельно соединённых элементов, как вероятность того, что хотя бы один из элементов будет исправен:
Если
Аналогично определяется надёжность работы 4-х и более параллельных элементов. Более просто определить величину «q(t)», а потом значение р(t)=1-q(t). Вероятность отказа 2-х элементов q=q1q2;3-х q=q1q2q3 а “n” элементов:
Если работающие параллельно элементы одинаковы по вероятности отказа, то:
qпар=qn; рпар=1-qn. (4.54)
Для параллельной работы группы элементов:
рпар=1-qпар=1-qn=1-(1-р)n, (4.55)
где р - надёжность 1-го элемента, т.е. вероятность безотказной работы. Если параллельно соединить “n” групп элементов, в каждой из которых “m” элементов работает последовательно (рис 4.4), то:
р1 рi
n
Рис.4.4
Надёжность одной цепи из m последовательных элементов из которых “в” элементов дублированы (рис 4.5):
Рис 4.5
где Pj – надёжность i-го не резервированного элемента; Pj – надёжность j-го резервированного элемента; а – число не дублированных элементов (а = m = в); m – число последовательно соединённых элементов; в – количество элементов дублированное из «m».
Надёжность системы из двух параллельных цепей (рис 4.6):
р
р
Рис.4.6
рпар=1-(1-р)2. (4.58)
где р – надёжность одной линии
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.164.176 (0.009 с.) |


 (4.30)
(4.30) (4.32)
(4.32)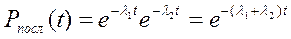 ; (4.34)
; (4.34) ; (4.35)
; (4.35) ; (4.36)
; (4.36) . (4.37)
. (4.37) - (4.38)
- (4.38)


 P1
P1
 . (4.39)
. (4.39) . (4.40)
. (4.40) >>
>>  (4.41)
(4.41) (4.42)
(4.42)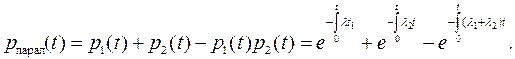 (4.43)
(4.43) ; (4.45)
; (4.45) . (4.46)
. (4.46)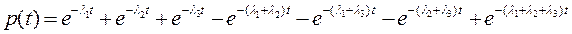 .(4.50)
.(4.50)
 :
: . (4.51)
. (4.51)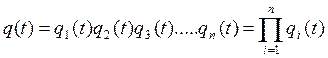 (4.52)
(4.52)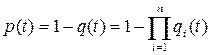 (4.53)
(4.53)

 (4.56)
(4.56)
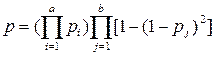 , (4.57)
, (4.57)



