
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы на основе выбора главного критерияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оценки по критериям. Типы шкал. В принятии решений различают шкалы непрерывных и дискретных оценок, количественных и качественных оценок. Кроме этой классификации существуют следующие типы шкал: 1) Шкала порядка. Оценки упорядочены по возрастанию или убыванию предпочтений ЛПР. Например, выбираем жилье. Выбираем район в котором жить. Для нас важна экологичность и так далее. Мы с вами выстраиваем районы в порядке нашего предпочтения. 2) Шкала равных интервалов (интервальная шкала). Она имеет равные расстояния по изменению качества между оценками. Начало отсчета и шаг для нее выбираются произвольно. 3) Шкала пропорциональных оценок (идеальная шкала).
Этапы процесса принятия решений: 1) Поиск информации. Собирается вся доступная на момент принятия решения информация (фактические данные, мнения экспертов и т.д.). На этом этапе строятся математические модели (если это возможно), проводятся опросы, определяется позиция активных групп и так далее. 2) Поиск и нахождение альтернатив. 3) Выбор лучшей альтернативы. Он включает в себя сравнение альтернатив и выбор лучшего варианта решения.
Типовые задачи принятия решений: 1) Упорядочение альтернатив. 2) Распределение альтернатив по классам решений. 3) Выделение лучшей альтернативы.
Постановка задачи принятия решений. формирование задачи выбора из некоторого множества: пусть Х - это множество альтернатив У - множество возможных последствий исходов, результатов Предполагается существование причинной связи между выбором некоторой альтернативы Хi ∈ Х и наступлению соответствующего исхода Уi ∈ У. Кроме этого предполагается наличие механизма оценки качества такого выбора. (Обычно оценивается качество исхода). Иногда возможно непосредственно оценить качество альтернативы Хi, тогда множество исходов выпадает из рассмотрения. Требуется выбрать наилучшую альтернативу для которой соответствующий исход имеет наилучшую оценку качества.
проведем анализ сформулированной задачи принятия решений. 1. Определение характера связи альтернатив с исходами. 1.1 Детерминированная связь. В этом случае существует однозначное отображение из множества Х в множество У с помощью оператора фи. То есть реализуется функция
1.2 Связь может иметь Вероятностный характер, когда выбор альтернативы Х определяет некоторую плотность распределения вероятностей на множестве У.
В этой ситуации задача называется “принятие решений (ПР) в условиях риска”. А первый случай (1.1) назывался принятие решений (ПР) в условиях определенности. Этот рисунок - взвешенный граф,характеризуется весом, то есть числом 1.3 Задача принятия решений в условиях полной неопределенности.
2. Задача ПР оценивается по количеству критериев: 2.1 Однокритериальные задачи (экстремум радость жизнь производная и тд.) 2.2 Многокритериальные задачи Что-то непонятное с фоток:
Классификация Паретто
Выбор множества Парето-оптимальных решений представляет собой отбор перспективных альтернатив, из которых затем отбирается лучшая. Множество Паретто представляет множество альтернатив, обладающих след свойством- любая из альтернатив, входящих в множество Паретто, хотя бы по одному критерию лучше любой другой альтернативы, входящее в это множество. Альтернатива А является доминирующей по отношению к альтернативе Б, если по всем критериям оценки альтернативы А не хуже, чем альтернативы Б, а хотя бы по одному критерию оценка А лучше, при этом альтернатива Б называется доминируемой. Выбор множества Парето производится следующим образом: все альтернативы попарно сравниваются друг с другом по всем критериям. Если при сравнении каких-либо альтернатив оказывается, что одна из них не лучше другой ни по одному критерию, то ее можно исключить из рассмотрения. Исключенную альтернативу не требуется сравнивать с другими альтернативами, т.к. она не перспективна. Выбор множества Парето не обеспечивает принятие окончательного решения, однако позволяет сократить количество рассматриваемых альтернатив, т.е. упрощает принятие решения.
ЯРКИЙ ПРИМЕР!!! Хим комбинат планирует внедрить комплекс средств автоматизации для управления технологическими процессами. Имеется возможность выбрать один из 7-ми вариантов (а1, а2 - а7). При выборе учитываются 4 критерия: к1 - затраты, связанные с изготовлением и вводом в эксплуатацию комплекса; к2 - срок ввода в эксплуатацию; к3 - срок гарантийного обслуживания предприятием- изготовителем; к4 - удобство комплекса в эксплуатацию
Выберем множество Парето: для этого выполним попарное сравнение альтернатив по всем критериям. Сравниваем а1 и а2: х(альтернативы, критерии) x(1,1)<x(2,1) x(1,2)=x(2,2) x(1,3)=x(2,3) x(1,4)<x(2,4) Таким образом х1 ни по одному критерию не лучше х2 -> х1 не включается в множество Парето. Сравниваем а2 и а3: х(альтернативы, критерии) x(2,1)>x(3,1) x(2,2)<x(3,2) x(2,3)<x(3,3) x(2,4)>x(3,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Сравниваем а2 и а4: х(альтернативы, критерии) x(2,1)>x(4,1) x(2,2)<x(4,2) x(2,3)<x(4,3) x(2,4)=x(4,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Сравниваем а2 и а5: х(альтернативы, критерии) x(2,1)>x(5,1) x(2,2)<x(5,2) x(2,3)=x(5,3) x(2,4)>x(5,4) Сравниваем а2 и а6: х(альтернативы, критерии) x(2,1)<x(6,1) x(2,2)=x(6,2) x(2,3)=x(6,3) x(2,4)>x(6,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Сравниваем а2 и а7: х(альтернативы, критерии) x(2,1)>x(7,1) x(2,2)<x(7,2) x(2,3)<x(7,3) x(2,4)>x(7,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Сравниваем а3 и а4: х(альтернативы, критерии) x(3,1)>x(4,1) x(3,2)=x(4,2) x(3,3)<x(4,3) x(3,4)<x(4,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Сравниваем а3 и а5: х(альтернативы, критерии) x(3,1)>x(5,1) x(3,2)>x(5,2) x(3,3)>x(5,3) x(3,4)>x(5,4) Таким образом х5 ни по одному критерию не лучше х3 -> х5 не включается в множество Парето. Сравниваем а3 и а6: х(альтернативы, критерии) x(3,1)<x(6,1) x(3,2)>x(6,2) x(3,3)>x(6,3) x(3,4)<x(6,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Сравниваем а3 и а7: х(альтернативы, критерии) x(3,1)>x(7,1) x(3,2)=x(7,2) x(3,3)=x(7,3) x(3,4)<x(7,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Сравниваем а4 и а6: х(альтернативы, критерии) x(4,1)<x(6,1) x(4,2)>x(6,2) x(4,3)>x(6,3) x(4,4)>x(6,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Сравниваем а4 и а7: х(альтернативы, критерии) x(4,1)<x(7,1) x(4,2)=x(7,2) x(4,3)>x(7,3) x(4,4)>x(7,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Сравниваем а6 и а7: х(альтернативы, критерии) x(6,1)>x(7,1) x(6,2)<x(7,2) x(6,3)<x(7,3) x(6,4)>x(7,4) Ни одна из альтернатив не исключается, т.к. лучше то одна, то другая. Множество Парето: а1, а3, а4, а6, а7. !!!ЯРКИЙ ПРИМЕР ЗАКОНЧИЛСЯ!!!!
Метод парных сравнений.
Чусова Юлия Сергеевна - след препод
Метод парных сравнений основан на попарном сравнении альтернатив. Для каждой пары альтернатив эксперт указывает, какая из альтернатив предпочтительнее.Существует ряд алгоритмов, реализующих метод парных сравнений. Они различаются по количеству используемых экспертных оценок (индивидуальные и коллективные оценки), по шкалам сравнения альтернатив и т.д.
Алгоритм Саати. Алгоритм основан на сравнении альтернатив, выполняемым одним экспертом. Для каждой пары альтернатив эксперт указывает, в какой степени одна из них предпочтительнее другой. Принятие решения на основе алгоритма Саати выполняется в следующем порядке: 1. экспертом заполняется матрица парных сравнений размером N*N, где N - количество альтернатив. Матрица заполняется по правилам:
Если i-я альтернатива менее предпочтительна, чем j-я, то указываются обратные оценки.Могут использоваться промежуточные оценки 2,4,6,8 и соответственно ½,¼,⅙. На главной диагонали матрицы ставятся 1.
2. находятся цены альтернатив Ci - среднее геометрические строк матрицы
3. Находится сумма C альтернатив 4. Находятся веса альтернатив
Пример: предприятие выбирает основной вид рекламы для новой продукции. Предлагается 4 возможных вида: реклама на телевидение (А1), на радио (А2), в газетах (А3) и на стендах (А4). Решение о выборе рекламы принимается на основе консультации с экспертом.
C = 3.71+0.54+1.7+0.29=6.24
Наиболее предпочтительной по мнению эксперта является альтернатива, имеющая максимальный вес. Таким образом наиболее эффективна реклама на телевидение, следующая за ней - в газетах, менее эффективна на радио и наименее эффективна на стендах. Для данного метода возможно проверка экспертных оценок на непротиворечивость. Она позволяет выявить ошибки, которые мог допустить эксперт при заполнении матрицы парных сравнений. 1. находятся суммы столбцов матрицы парных сравнений Rj 2. рассчитывается вспомогательная величина лямбда путем суммирования произведений сумм столбцов матрицы на веса альтернатив 3. находится величина, называемая индексом согласованности, 4. в зависимости от размерности матрицы парных сравнений находится величина случайной согласованности СлС из таблицы.
5. находится отношение согласованности Если отношение согласованности более 0,2, то требуется уточнение матрицы парных сравнений.
Проверим пример. 1. нижняя строка таблицы 2. 3. 4. Слс = 0,9 5. ОС = 0,03/0,9=0,033 ОС < 0,2 -> уточнение экспертных оценок в данном случае не требуется.
Алгоритм парных сравнений для группы экспертов.
Каждый из экспертов выполняет сравнение альтернатив независимо от других. Для каждой пары альтернатив эксперт указывает, в какой степени одна из них предпочтительнее другой.
Пример: предприятие, выпускающее металлоизделия ищет способы снижения потерь из отходов металла. Предлагается 4 способа: изменить технологический процесс, чтобы снизить количество отходов (А1), перейти на выпуск новых изделий, при выпуске которых отходов меньше (А2), создать подсобное производство и использовать отходы в качестве сырья (А3) и продавать отходы (А4). Решение принимается с участием 3 экспертов. Мнение первого эксперта: лучшее решение А3, немного хуже А4, значительно хуже А1, совсем плохой А2. Мнение второго эксперта: лучшее решение А4, немного хуже А1, еще хуже А3 и совсем плохое А2 Мнение третьего эксперта: лучшее решение А3, немного хуже А1, значительно хуже А4 и совсем плохое А2. Выбор решения выполняется в следующем порядке: 1. каждый из экспертов заполняет матрицу парных сравнений размером N*N. Матрица заполняется по следующим правилам: a. элемент Xij указывает, в какой степени по мнению эксперта i-я альтернатива является более предпочтительной по сравнению с j-й. Степень предпочтения указывается в долях единицы. Если i-я альтернатива лучше j-й, то Xij больше чем 0,5. Чем больше превосходство, тем ближе Xij к единицы. Если i-я альтернатива хуже j-йЮ то Xij меньше 0,5 и чем больше превосходство j-й альтернативы, тем ближе Xij к нулю.
А3 -> А4 -> А1 ->А2
А4 -> А1 -> А3 -> А2
А3 -> А1 -> А4 -> А2
2. Определяются оценки предпочтения альтернатив над другими по мнению каждого эксперта. 3. Определяются обобщенные оценки предпочтения альтернатив над другими с учетом мнения всех экспертов
4. Находится сумма всех оценок C = 4.8 + 1.1 + 6.3 + 5.8 = 18 5. Находятся веса всех альтернатив
Т.о. чем выше вес, тем лучше альтернатива -> лучше решение - создать подсобное производство. Немного худшее - продать отходы. Значительно хуже - изменить технологический процесс. Совсем плохо - перейти на выпуск новых изделий с меньшими отходами
Метод предпочтений
Основан на ранжировании альтернатив, выполненном группой экспертов. Каждый из экспертов независимо от других указывает какая из альтернатив является лучшей, какая следующей и т.д. Пример: В ходе разработки плана мероприятий по повышению эффективности производства возникает задача определить степень влияния разных факторов на производительность труда. Требуется определить влияние на производительность труда следующих факторов: уровень профессиональной подготовки рабочих (А1), соблюдение технологической дисциплины (А2), эффективность материальных стимулов (А3), эффективность организации соревнований (А4), технологическое переообрежение (А5). Оценка влияния факторов выполняется 4-мя экспертами. Алгоритм: 1. каждому эксперту предлагается выполнить ранжирование альтернатив по предпочтению. В данном примере каждый эксперт присваивает номер 1 фактору, который по его мнению оказывает наибольшее влияние на рост производительности труда, номер 2 - следующему по важности и т.д. Оценки каждого эксперта сводятся в таблицу размером M*N, где M - количество экспертов, N - количество альтернатив.
2. Производится преобразование матрицы оценок по формуле
3. Находим суммы преобразованных оценок по каждой из альтернатив 4. Находятся суммы всех оценок 5. Находятся веса альтернатив
Чем больше вес, тем более предпочтительной является альтернатива по мнению эксперта. В данном примере самым важным фактором, влияющим на производительность труда является уровень профессиональной подготовки рабочих, следующий по важности - соблюдение технологической дисциплины и т.д. A1->A2->A3->A5->A4 При использовании метода предпочтений имеется возможность проверки согласованности экспертной оценки. Если мнения экспертов резко разнятся, то, возможно, требуется повторить их опрос и уточнить оценки. Для проверки согласованности мнений экспертов вычисляется величина, называемая коэффициентов конкордации W. Ее расчет выполняется в следующем порядке: 1. Находится сумма оценок, указанных экспертами, для каждой альтернативы 2. Находится вспомогательная величина A. 3. Находится вспомогательная величина S 4. Находится коэффициент конкордации При
Т.к.
Метод ранга Метод основан на балльных оценках альтернатив, указанных несколькими экспертами. Каждый из экспертов независимо от других оценивает альтернативы по некоторой шкале (обычно 10-балльной). Чем более предпочтительна по мнению эксперта является альтернатива. тем более высокий балл для нее указывается. Пример: оценим влияние факторов на производство труда (предыдущий пример). 1. Каждый эксперт указывает оценки альтернатив по 10 балльной шкале. Они сводятся в матрице M*N
2. Находится суммарная оценка альтернатив всеми экспертами 3. Находится сумма всех оценок 4. Находятся веса альтернатив Для данного метода также возможно проверка экспертной оценки согласованности. Для этого рассчитаем дисперсию (оценку разброса) оценки для каждого эксперта и для каждой альтернативы. Расчет выполняется в следующем порядке: 1. Находится средняя оценка каждой альтернативы
2. Находится дисперсия оценок экспертов. N = 5
и т.д. 3. Находится дисперсия оценок каждой альтернативы
и т.д. Если величина Методы принятия решений для слабоструктурированных задач. Оценки по критериям. Типы шкал. В принятии решений различают шкалы непрерывных и дискретных оценок, количественных и качественных оценок. Кроме этой классификации существуют следующие типы шкал: 1) Шкала порядка. Оценки упорядочены по возрастанию или убыванию предпочтений ЛПР. Например, выбираем жилье. Выбираем район в котором жить. Для нас важна экологичность и так далее. Мы с вами выстраиваем районы в порядке нашего предпочтения. 2) Шкала равных интервалов (интервальная шкала). Она имеет равные расстояния по изменению качества между оценками. Начало отсчета и шаг для нее выбираются произвольно. 3) Шкала пропорциональных оценок (идеальная шкала).
Этапы процесса принятия решений: 1) Поиск информации. Собирается вся доступная на момент принятия решения информация (фактические данные, мнения экспертов и т.д.). На этом этапе строятся математические модели (если это возможно), проводятся опросы, определяется позиция активных групп и так далее. 2) Поиск и нахождение альтернатив. 3) Выбор лучшей альтернативы. Он включает в себя сравнение альтернатив и выбор лучшего варианта решения.
Типовые задачи принятия решений: 1) Упорядочение альтернатив. 2) Распределение альтернатив по классам решений. 3) Выделение лучшей альтернативы.
Постановка задачи принятия решений. формирование задачи выбора из некоторого множества: пусть Х - это множество альтернатив У - множество возможных последствий исходов, результатов Предполагается существование причинной связи между выбором некоторой альтернативы Хi ∈ Х и наступлению соответствующего исхода Уi ∈ У. Кроме этого предполагается наличие механизма оценки качества такого выбора. (Обычно оценивается качество исхода). Иногда возможно непосредственно оценить качество альтернативы Хi, тогда множество исходов выпадает из рассмотрения. Требуется выбрать наилучшую альтернативу для которой соответствующий исход имеет наилучшую оценку качества.
проведем анализ сформулированной задачи принятия решений. 1. Определение характера связи альтернатив с исходами. 1.1 Детерминированная связь. В этом случае существует однозначное отображение из множества Х в множество У с помощью оператора фи. То есть реализуется функция
1.2 Связь может иметь Вероятностный характер, когда выбор альтернативы Х определяет некоторую плотность распределения вероятностей на множестве У.
В этой ситуации задача называется “принятие решений (ПР) в условиях риска”. А первый случай (1.1) назывался принятие решений (ПР) в условиях определенности. Этот рисунок - взвешенный граф,характеризуется весом, то есть числом 1.3 Задача принятия решений в условиях полной неопределенности.
2. Задача ПР оценивается по количеству критериев: 2.1 Однокритериальные задачи (экстремум радость жизнь производная и тд.) 2.2 Многокритериальные задачи Что-то непонятное с фоток:
Методы на основе выбора главного критерия К этому классу относятся все методы, в которых выбор решения производится на основе одного (главного) критерия. На остальные критерии, как правило, накладываются ограничения. К этому же классу следует отнести методы, называемые “методами на основе лексикографического упорядочения критериев”. В этих методах сначала выбирается лучшая альтернатива по одному (наиболее важному) критерию. Если выбранных альтернатив оказывается больше, чем одна, то используется следующий по важности критерий и т.д. Такие методы не применимы для задач, в которых требуется учитывать несколько критериев, близких по важности.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.239.70 (0.013 с.) |


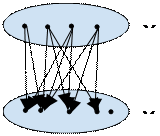
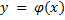 . И в этом случае у нас граф связи альтернатив с исходами будет выглядеть следующим образом:
. И в этом случае у нас граф связи альтернатив с исходами будет выглядеть следующим образом: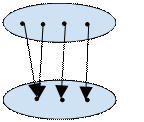
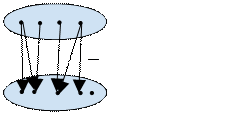
 - вероятностью наступления исхода У при выборе альтернативы Х.
- вероятностью наступления исхода У при выборе альтернативы Х. 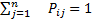
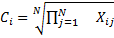 .Т.е. элементы строки перемножаются и из их произведения извлекается корень степени N.
.Т.е. элементы строки перемножаются и из их произведения извлекается корень степени N.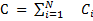
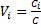
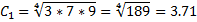
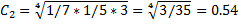
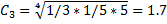
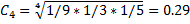
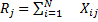
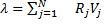
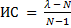
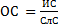
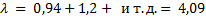
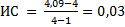
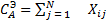 (сумма строк матрица
(сумма строк матрица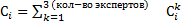 , i - номер альтернативы
, i - номер альтернативы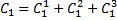
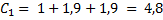
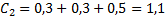
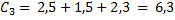
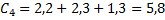
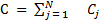
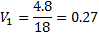
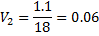
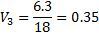
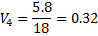
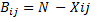
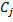
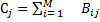
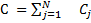
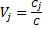
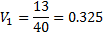
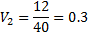
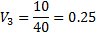
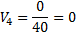
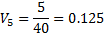
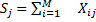
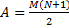
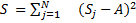
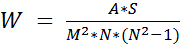
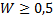 степень согласованности экспертных оценок может считаться достаточной. При
степень согласованности экспертных оценок может считаться достаточной. При 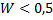 требуется уточнение и согласование экспертных оценок.
требуется уточнение и согласование экспертных оценок.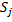
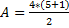 =12
=12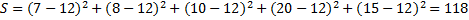
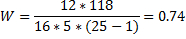
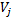
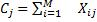 (Сумма по столбцам)
(Сумма по столбцам)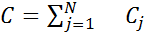
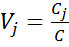 Наиболее предпочтительной является альтернатива, имеющая максимальный вес -> A1->A2->A3->A5->A4
Наиболее предпочтительной является альтернатива, имеющая максимальный вес -> A1->A2->A3->A5->A4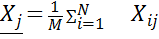 ,
, 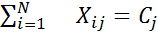 , M=4, i - номер строки, j - номер столбца
, M=4, i - номер строки, j - номер столбца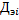
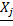
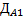
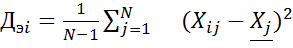
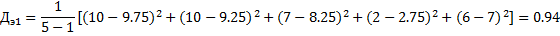
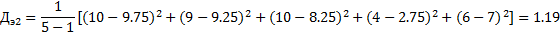
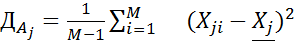
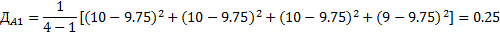
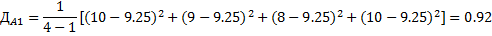
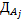 (оценка j-й альтернативы у экспертов сильно отличается), то следует проанализировать причину таких расхождений. В нашем примере A3.
(оценка j-й альтернативы у экспертов сильно отличается), то следует проанализировать причину таких расхождений. В нашем примере A3.


