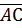Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И 7.Независимость аксиом и полнота систем аксиом.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Акс. теория дедуктивно полная. результат доказуемости аксиом бывает трехвозможен: 1утверждение истинно 2утв недоказуемо 3утв ложно Полнота<=>категоричность. акс теория назкатигоричной если все ее модели изоморфны(т.е. если между основными эл-тами этих моделей можно установить взаимооднозн. отнош,при кот. сохраняются основные отнош) Матем теории:1котегоричные. 2 некотегоричные:2.1топология 2.2 теория групп Способы исследования:1исходя из системы аксеом 2 любой модели Акс теория описана конечным списком аксеом существует много зависимых аксеом.это проверяется с помощью моделей: 1не Аn-отрицание 2(буква сигма штрих по Т):А1...,Аn-1, не Аn если мы докажем то можем построить след модель:(буква сигма поR=>буква сигма поT,буква сигма поR=>буква сигма поT) если Аn и не Аn независимы, то буква сигма по r -противоречива, т.к. выполняется Аn и не Аn.
Аксиоматика Вейля Другое наз. Точечно-векторная аксиоматика. Структура евклидовой геометрии в аксиоматике Вейля это <
1. Группа: аксиомы векторного пространства А1: A2: A3: A4: A5: A6: k( A7: (k A8: 2. Группа: dim v=n n=1 - прямая n=2 -плоскость n=3 –трехмерное пространство Размерность равномерно и означает, что в 3. Группы скалярного произведения
A10: A11: A12: A13: 4. Группа
A, B –точки A14: Единственность откладывания вектора
Непротиворечивость аксиоматики Вейля Непротиворечивость Gw аксиоматики Вейля подходит для метода координат и арифметическая модель Gw основывается на методе координат Для простоты возьмём планиметрию n=2 IR – теория действ. чисел U - теория на которой строится модель E=IR2={(x,y)|x,y ͼ IR} U=IR2={(a1a2)|a1a2 ͼ IR} (+) (a1a2)+(b1b2)=(a1+b1,a2+b2)
A1: a+b=(a1,a2)+(b1b2)=(a1+b1,a2+b2)= (b1+a1, b2+a2)=(b1b2)+ (a1a2) 0=(0,0); -a=(-a1,-a2) (.) ka=k(a1a2)= (ka1ka2)
A8: k(a+b)=k[(a1a2)+ (b1b2)]=k(a1+b1,a2+b2)=(ka1+kb1,ka2+kb2)=(ka1ka2)+(kb1kb2)= k(a1a2)+ k(b1b2)=ka+kb Vгр. L1=(1,0) L2=(0,1) тогдалюбойвектор a =(a1,a2)=a1(1,0)+a2(0,1)= a1L1+ a2L2 k1L1+ k2L2=0 0=k1L1+ k2L2= k1(1,0)+k2(0,1)= (k1,0)+(0, k2)=(k1 k2)=(0,0)=0 ó k1=0 и k2=0 вбаз.(L1 L2) dim U=1 a=(a1,a2) b=(b1b2) a+b=def= a1b1+a2b2 aa=((a1,a2) (a1,a2))=a12+ a22≥0 a12+ a22=0 ó a1=a2=0 a=(0,0) ч.т.д A=(x1y1) B=(x2y2) G(A,B)=AB=(x2-x1,y2-y1) A14: A=(x1y1), a=(a1,a2) Ǝ! B=(x1+ a1, y2+ a2) AB=a C=(x3y3) AB+BC=(x2-x1,y2-y1)+ (x3-x2,y3-y2)= (x2-x1+ x3-x2,y2-y1+ y3-y2)= (x3-x1,y3-y1)=AC Таким образом построена модель Gw Евклидовой плоскости на основе теории IR. Это означает, что аксиомы Gw непротиворечивы, если не противоречива теория IR.
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.236.173 (0.009 с.) |

 >
> - пространство точек
- пространство точек - векторное пространство
- векторное пространство сложение векторов
сложение векторов умножение векторов
умножение векторов -скалярное произведение
-скалярное произведение -откладывание векторов
-откладывание векторов
 )+
)+  =
=  +
+ 

 :
: 

 )= (k
)= (k  , k
, k 
 =
= 

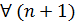 вектор линейно-независимый
вектор линейно-независимый

 =
= 
 +
+ 
 =
= 



 Основное свойство сложения векторов
Основное свойство сложения векторов  +
+  =
=