
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угол параллельности. Взаимное расположение прямых на плоскости ЛобачевскогоСодержание книги
Поиск на нашем сайте
1) Пересечение l1 и l2 2) Параллельные l1 и l2
3) l1 и l2 расходящиеся
А А- угол параллельности в евклидовой геометрии Всегда α=
Модель Клейна III2. Данное определение неевклидовой геометрии Л2: Удобно определять неевклид движения через преобразования (проективные, гиперболические, гомологии). F(A|→A) – l-ось гомологии, Р – центр. \ Строим образ. Р?АА|, Р?BB|, ۷A,B Если точка М=АА ∩l, то (РМ,АА´)=1 ↔ f2=id или f=f-1, f – инволюция.
Гиперболические гомологии f2=id получаются, если l и Р – поляра и полюс относительно овала ξ. ABCD – полный 4-хугольник, вписанный в овал.
A,B,C,D - вершины P,Q,R’ – диагональные точки PR=l, (MN,RQ)=-1, (LL’,RQ)=-1 PL=m, PL’=m’ – касательные PQR – автополярный треугольник, каждая сторона которого, явл полярой противоположной вершины. Все неевклид движения 1-го рода явл композицией симметрий. Sl=f Элементы геометрии Лобачевского в модели Клейна 1. L-поляра Р f=SL–неевклид.симметрия f(А)= А1 А А1=m Полюс m и точка Q g=Sm (неевклидова симметрия) то g(U)=U! =V Cледовательно, <AO1 Uà<AO1 V,AO1 2. U1P,V1P-касательные кси. O1Р-биссектриса неевклидова. Если О=О1, то евклидова и неевклидова биссектрисы совпадут, И преобразуют один угол в другой и учитывая что касательные переходят в касательные будет следов., что O1Р-неевкл.биссектриса. 3. Еслиf=SL-неевклид.симметрия, R (из св-в полного 4-х верш.И гомологии) [MR]à[NR].Следов., неевклиддлинны этих отрезков равны, R-неевклидова середина [MN]. 4. Если треуг.АВС в модели Клейна продолжить Сторону до пересечения с абсолютом и построим биссектрисы углов А,В, С,тогда из т. Брианшона следует,чтонеевклид.биссектриссы пересек в одной точке 5. АР,ВР,СР перпенд.L.тогда все перпендикуляры к L пересек.в полюсе Р.Следов, все перпенд между собой расх. 6. L1||L, mперпендик.L, L1 должна проходить через Р и Q,т.е. mвключ в PQ(проект прямая). т.к.PQкасат. к кси, то PQ в пересе с L2= пустое множество. Следов., общего перпенд к 2-м параллельным прямым нет. 7. L1иL-расход, пересек в точкеР, тогда общий перпенд.m к L1иL должен принадлежать RQ.Следов.,онсущ и единств.,m пересек с L2. 8. 1) если АВ и СD параллельны, то к ним общего перпенд нет. 2) если АВ и СD расход, то общий перпенд к ним только один.Или АDперпенд. АВ, СД, или ВС перпенд АВ, СД.Следов.,4-ник не Может быть прямоугольником, т.е. в плоскости Лобачевского не существует прямоугольников.
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.137.96 (0.009 с.) |




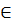 L(по т.взаимости проект геометрии)à
L(по т.взаимости проект геометрии)à


