Элементы заголовков в списках; нелинейные связные структуры.

Элементы заголовков в списках

Для создания списка с заголовком в начало списка вводится дополнительный элемент, который может содержать информацию о списке.

 

Нелинейные связанные структуры

Двусвязный список может быть нелинейной структурой данных, если вторые указатели задают произвольный порядок следования элементов.

 

 

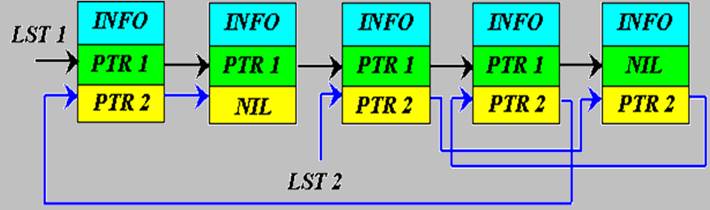
LST1 - указатель на начало первого списка (ориентированного указателемями PTR1). Он линейный и состоит из 5-и элементов.

Второй список образован из этих же самых элементов, но в произвольной последовательности. Началом 2-го списка является 3-й элемент, а концом 2-ой элемент.

В общем случае элемент списочной структуры может содержать сколь угодно много указателей, то есть может указывать на любое количество элементов.

Можно выделить 3 признака отличия нелинейной структуры:

1) Любой элемент структуры может ссылаться на любое число других элементов структуры, то есть может иметь любое число полей-указателей.

2) На данный элемент структуры может ссылаться любое число других элементов этой структуры.

3) Ссылки могут иметь вес, то есть подразумевается иерархия ссылок.

Пример моделирования с помощью нелинейного списка

Пусть имеется дискретная система, в графе состояния которой узлы - это состояния, а ребра - переходы из состояния в состояние.

 

 

Входной сигнал в систему это X. Реакцией на входной сигнал является выработка выходного сигнала Y и переход в соответствующее состояние.

Граф состояния дискретной системы можно представить в виде двусвязного нелинейного списка. При этом в информационных полях должна записываться информация о состояниях системы и ребрах. Указатели элементов должны формировать логические ребра системы

Для реализации вышесказанного:

1) должен быть создан список, отображающий состояния системы (1, 2, 3);

2) должны быть созданы списки, отображающие переходы по ребрам из соответствующих состояний.

Реализация графа в виде нелинейного списка можно представить рисунка ниже:

 

 

В общем случае при реализации многосвязной структуры получается сеть.

 

Понятие рекурсивных структур данных. Деревья, их признаки и представления.

Рассмотрим рекурсивные алгоритмы и рекурсивные структуры данных.

Рекурсия - процесс, протекание которого связано с обращением к самому себе (к этому же процессу).

Пример рекурсивной структуры данных - структура данных, элементы которой являются такими же структурами данных

 

 

 

Деревья

Дерево - нелинейная связанная структура данных

Дерево характеризуется следующими признаками:

- дерево имеет один элемент, на который нет ссылок от других элементов. Этот элемент называется корнем дерева;

- в дереве можно обратиться к любому элементу путем прохождения конечного числа ссылок (указателей);

- каждый элемент дерева связан только с одним предыдущим элементом.

Любой узел дерева может быть промежуточным либо терминальным (листом). На рисунке промежуточными являются элементы M1, M2; листьями - A, B, C, D, E. Характерной особенностью терминального узла является отсутствие ветвей.

 

Высота дерева - это количество уровней дерева. У дерева на рисунке высота равна двум.

 

Количество ветвей, растущих из узла дерева, называется степенью исхода узла (на рисунке для M1 степень исхода 2, для М2 - 3).

 

Для описания связей между узлами дерева применяют также следующую терминологию: М1 - “отец” для элементов А и В. А и В - “сыновья” узла М1.

Деревья могут классифицироваться по степени исхода:

1) если максимальная степень исхода равна m, то это - m-арное дерево;

2) если степень исхода равна либо 0, либо m, то это - полное m-арное дерево;

3) если максимальная степень исхода равна 2, то это - бинарное дерево;

4) если степень исхода равна либо 0, либо 2, то это - полное бинарное дерево.

Представление деревьев

 

Наиболее удобно деревья представлять в памяти ЭВМ в виде связанных списков. Элемент списка должен содержать информационные поля, в которых могут содержаться значение ключа узла и другая хранимая информация, а также поля-указатели, число которых равно степени исхода.

 

 

 

Бинарные деревья

Согласно представлению деревьев в памяти ЭВМ каждый элемент бинарного дерева является записью, содержащей четыре поля. Значения этих полей - соответственно ключ записи, текст записи, ссылка на элемент влево – вниз и ссылка на элемент вправо – вниз.

Бинарные деревья являются наиболее используемой разновидностью деревьев.

Формат элемента бинарного дерева представлен на рисунке ниже

 

Функция создания элемента бинарного дерева V = MakeTree (key, rec)

V - указатель на создаваемый элемент динамической структуры

Алгоритм функции Maketree(key,rec)

p = getnode

r (p) = rec

k (p) = key

v = p

left (v)= nil

right (v) = nil

return

Операция V = MakeTree(Key, Rec) - создает элемент (узел дерева) с двумя указателями и двумя полями (ключевым и информационным).

 

Упорядочное бинарное дерево

В упорядоченном бинарном дереве левый сын имеет ключ меньший, чем у отца, а значение ключа правого сына больше значения ключа отца.

Построим бинарное дерево из следующих элементов: 50, 46, 61, 48, 29, 55, 79.

 

 

Получено идеально сбалансированное дерево - дерево, в котором левое и правое поддеревья имеют уровни, отличающиеся не более чем на единицу.