Сравнительный анализ эффективности методов сортировки.

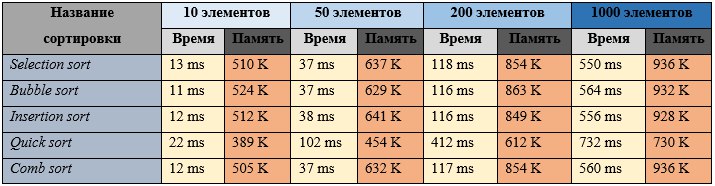
Для проведения исследования были выбраны следующие алгоритмы сортировки:

Selection sort (сортировка выбором) – суть алгоритма заключается в проходе по массиву от начала до конца в поиске минимального элемента массива и перемещении его в начало. Сложность такого алгоритма O(n2).

Bubble sort (сортировка пузырьком) – данный алгоритм меняет местами два соседних элемента, если первый элемент массива больше второго. Так происходит до тех пор, пока алгоритм не обменяет местами все неотсортированные элементы. Сложность данного алгоритма сортировки равна O(n^2).

Insertion sort (сортировка вставками) – алгоритм сортирует массив по мере прохождения по его элементам. На каждой итерации берется элемент и сравнивается с каждым элементом в уже отсортированной части массива, таким образом находя «свое место», после чего элемент вставляется на свою позицию. Так происходит до тех пор, пока алгоритм не пройдет по всему массиву. На выходе получим отсортированный массив. Сложность данного алгоритма равна O(n^2).

Quick sort (быстрая сортировка) – суть алгоритма заключается в разделении массива на два под-массива, средней линией считается элемент, который находится в самом центре массива. В ходе работы алгоритма элементы, меньшие чем средний будут перемещены в лево, а большие в право. Такое же действие будет происходить рекурсивно и с под-массива, они будут разделяться на еще два под-массива до тех пор, пока не будет чего разделать (останется один элемент). На выходе получим отсортированный массив. Сложность алгоритма зависит от входных данных и в лучшем случае будет равняться O(n×2log2n). В худшем случае O(n^2). Существует также среднее значение, это O(n×log2n).

Comb sort (сортировка расческой) – идея работы алгоритма крайне похожа на сортировку обменом, но главным отличием является то, что сравниваются не два соседних элемента, а элементы на промежутке, к примеру, в пять элементов. Это обеспечивает от избавления мелких значений в конце, что способствует ускорению сортировки в крупных массивах. Первая итерация совершается с шагом, рассчитанным по формуле (размер массива)/(фактор уменьшения), где фактор уменьшения равен приблизительно 1,247330950103979, или округлено до 1,3. Вторая и последующие итерации будут проходить с шагом (текущий шаг)/(фактор уменьшения) и будут происходить до тех пор, пока шаг не будет равен единице. Практически в любом случае сложность алгоритма равняется O(n×log2n).

Для проведения тестирования будет произведено по 5 запусков каждого алгоритма и выбрано наилучшее время. Наилучшее время и используемая при этом память будут занесены в таблицу. Также будет проведено тестирование скорости сортировки массива размером в 10, 50, 200 и 1000 элементов чтобы определить для каких задач предназначен конкретный алгоритм.

Полностью неотсортированный массив:

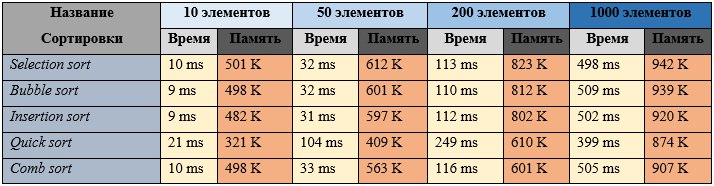
Частично отсортированный массив (половина элементов упорядочена):

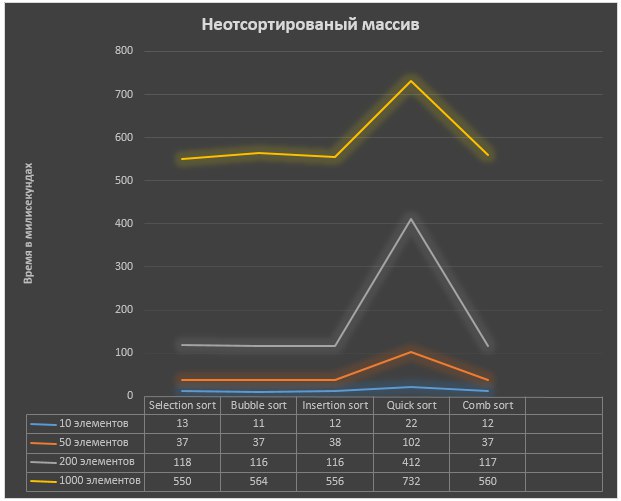
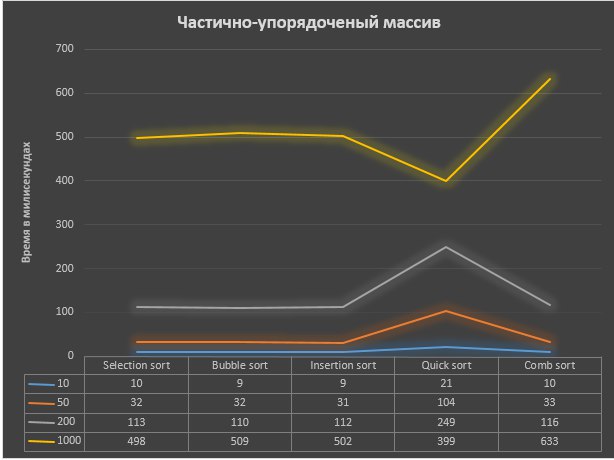
Результаты, предоставленые в графиках:

Выводы:

В результате проведенного исследования и полученных данных, для сортировки неотсортированного массива, наиболее оптимальным из представленных алгоритмов для сортировки массива является быстрая сортировка. Несмотря на более длительное время выполнения алгоритм потребляет меньше памяти, что может быть важным в крупных проектах. Однако такие алгоритмы как сортировка выбором, обменом и вставками могут лучше подойти для научных целей, например, в обучении, где не нужно обрабатывать огромное количество данных. При частично отсортированном массиве результаты не сильно отличаются, все алгоритмы сортировки показывают время примерно на 2-3 миллисекунды меньше. Однако при сортировке частично отсортированного массива быстрая сортировка срабатывает намного быстрее и потребляет меньшее количество памяти.