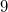Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление целых и действительных чисел в позиционных системах счисленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера. Число с плавающей запятой состоит из набора отдельных двоичных разрядов, условно разделенных на так называемые знак (англ. sign), порядок (англ. exponent) и мантиссу (англ. mantis). В наиболее распространённом формате (стандарт IEEE 754) число с плавающей запятой представляется в виде набора битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа (
§ § § § Порядок также иногда называют экспонентой или просто показателем степени. При этом лишь некоторые из вещественных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями.
56. Связь между системами счисления с основаниями вида 2k Перевод чисел между системами счисления, основания которых являются степенями числа 2, может производиться более простым алгоритмом. Для записи двоичных чисел используют две цифры, то есть в каждом разряде числа возможны два варианта записи. Для записи восьмеричных чисел используется восемь цифр, то есть возможны восемь вариантов. А для записи шестнадцатеричных чисел используется 16 цифр, то есть 16 возможных вариантов. Таким образом, для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то нужно его дополнить нулями слева. Ну типа как на ЕГЭ. Например, преобразуем дробное двоичное число А 2 = 0,1101012 в восьмеричную систему счисления:
Получаем: А 8 = 0,658.
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.146.94 (0.006 с.) |

 — если число положительное,
— если число положительное,  — если число отрицательное). При этом порядок записывается как целое число в коде со сдвигом, а мантисса — в нормализованном виде (от 1 до 10), своей дробной частью в двоичной системе счисления. Знак — один бит, указывающий знак всего числа с плавающей точкой. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой в следующем виде:
— если число отрицательное). При этом порядок записывается как целое число в коде со сдвигом, а мантисса — в нормализованном виде (от 1 до 10), своей дробной частью в двоичной системе счисления. Знак — один бит, указывающий знак всего числа с плавающей точкой. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой в следующем виде: , где
, где  — знак,
— знак,  — основание,
— основание, 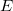 — порядок, а
— порядок, а  — мантисса. Десятичное число, записываемое как
— мантисса. Десятичное число, записываемое как 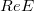 , где
, где 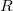 — число в полуинтервале
— число в полуинтервале  ,
,  ; в нормализированной форме модуль
; в нормализированной форме модуль