Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая постановка задач линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Линейное программирование – это раздел математики ориентируемый на нахождении экстремума в задачах, которые описываются линейными уравнениями.
Задачей линейного программирования называется задачей исследования операций, математическая модель которой имеет вид:
F(x) =
Целевая функция (2) - линейная форма.
или
Все переменные должны быть xj ≥ 0, j = Система (4) - система ограничений задачи линейного программирования (ЗЛП). Если математическая модель ЗЛП имеет вид:
xj ≥ 0, bi ≥ 0, то ЗЛП представлена в канонической форме.
2.3.2 Построение математических моделей задач линейного программирования
Рассмотрим процесс построения математических моделей ЗЛП на примерах.
Пример 1 - Задача о диете
Из имеющихся в распоряжении видов пищи нужно составить такую диету, которая, с одной стороны, обеспечивала бы удовлетворение минимальных потребностей организма в питательных веществах (белках, жирах, углеводах, витаминах и т.д.) и вместе с тем требовала бы наименьших затрат. Рассмотрим простую математическую модель этой задачи. Пусть имеются два вида продуктов, П1 и П2, содержащих питательные вещества А, В, С. Известно, сколько питательных веществ того или иного вида содержится в 1 кг пищи П1 или П2; эти сведения указаны в таблице 2.
Таблица 2 – Условие задачи о диете
Кроме этих данных, нам известны; a, b, c – ежесуточная потребность организма в А, В, С (соответственно) и s1 и s2 – стоимость 1 кг пищи П1, П2 (соответственно). Требуется рассчитать количество х1 продукта П1 и количество х2 продукта П2 так, чтобы обеспечить необходимое количество питательных веществ при минимальных затратах на пищу. Очевидно, общая стоимость пищи будет S = s1x1 + s2x2. Общее количество вещества А в обоих видах пищи равно a1x1 + a2x2. Оно должно быть не меньше а: a1x1 + a2x2³ a. Аналогичные неравенства должны выполняться для Ви С: b1x1 + b2x2 ³ b, c1x1+ с2х2 ³ с.
Таким образом, приходим к следующей задаче. Дана система трех линейных неравенств с двумя неизвестными х1, х2и линейная функция S = s1x1 + s2x2 (6).
b1x1 + b2x2 ³ b (6) c1x1 + c2x2 ³ c
Требуется среди неотрицательных решений (х1, х2)системы (6) выбрать такое, при котором функция S, достигает наименьшего значения (минимизируется).
Пример 2 - Задача о распределения ресурсов
Предприятие имеет в своем распоряжении определенное количество ресурсов (сырье, оборудование и т.д.), из этих ресурсов выпускается определенное количество товаров. Известно количество единиц каждого из ресурсов, используемых при производстве единицы каждого вида товара. Известен также доход, полученный предприятием от выпуска одной единицы товара. При этих условиях требуется выпустить такое количество товаров, чтобы доход их был максимальным.
Пусть предприятие имеет 3 вида ресурсов: R1, R2, R3 в количестве b1, b2, b3 единиц соответственно (таблица 3). Предприятие выпускает товары 2 видов: Т1 и Т2. Известно, что аij – количество единиц ресурса Ri, используемого для выпуска 1 единицы товара Tj и с1, с2 – доход от 1 единицы товара Т1 и Т2. При этих условиях требуется выпустить количество товаров Т1 и Т2, чтобы доход был максимальным.
Таблица 3 – Условие задачи о распределении ресурсов
Обозначим: x1 – количество товара T1; x2 – количество товара T2 x1 ≥ 0, x2 ≥ 0 Для выпуска товаров с использованием ресурса R1 понадобиться следующее количество единиц этого ресурса: Из условия задачи составим систему ограничений (7).
Составим линейную форму: F(x) = с1x1 + с2x2 → max Требуется среди неотрицательных решений (х1, х2)системы (7) выбрать такое, при котором функция F, достигает наибольшего значения (максимизируется). К подобным схемам могут быть сведены различные задачи о составлении сплавов, смесей горючего, задачи об определении состава животноводческих кормовых смесей наименьшей стоимости, о составлении смеси химических удобрений и т. д.
Пример 3 - Транспортная задача
Уголь, добываемый в нескольких месторождениях, отправляется ряду потребителей: заводам, электростанциям и т. п. Известно, сколько угля добывается в каждом из месторождений, скажем, за месяц, и сколько его требуется на тот же срок любому из потребителей. Известны расстояния между месторождениями и потребителями, а также условия сообщения между ними; учитывая эти данные, можно подсчитать, во что обходится перевозка каждой тонны угля из любого месторождения в любой пункт потребления. Требуется при этих условиях спланировать перевозки угля таким образом, чтобы затраты на них были минимальными. Примем, что имеются лишь два месторождения М1 М2 и три потребителя П1 П2, П3. Количества угля в М1 и М2равны соответственно a1 и а2; потребности пунктов П1 П2, П3пусть будут соответственно b1, b2, b3 - Будем считать, что суммарные запасы равны суммарным потребностям: a1+ а2 = b1+b2+ b3.Наконец, заданы числа Сij(i = 1, 2; j= 1, 2, 3) - стоимости перевозки тонны угля из Мiв ПjЗадача состоит в нахождении шести чисел x11, x12, x13, x21, x22, x23, где хij-количество угля, предназначенное к отправке из Мi в Пj. Для удобства обозрения составим таблицу 4.
Таблица 4 – Транспортная задача
Общее количество угля, вывезенное из М1должно равняться а1;отсюда имеем условие x11+ x12+ x13= a1 Аналогичное условие должно выполняться для М2: x21+ x22 + x23= a2. Общее количество угля, привезенное в П1должно равняться b1; отсюда x11+ x21= b1. Аналогично получаем условия: x12+ x22= b2, x13+ x23= b3. Предполагаем, что стоимость перевозки прямо пропорциональна количеству перевозимого угля, т.е. перевозка из Miв Пjстоит cij∙хij. Тогда общая стоимость всех перевозок будетS=c11x11+c12x12+c13x13+c21x21+c22x22+c23x23
Дана система (8)
x21 + x22 + x23 = a2, (8) x11 + x21 = b1, x12 + x22 = b2, x13 + x23 = b3.
и линейная функция S=c11x11+c12x12+c13x13+c21x21+c22x22+c23x23. Требуется среди неотрицательных решений x11, x12, x13, x21, x22, x23 системы (8) выбрать такое, при котором функция S достигает наименьшего значения (минимизируется).
2.3.3 Графическое решение задач линейного программирования
Графический способ решения ЗЛП целесообразно использовать для решения задач с двумя переменными, когда ограничения выражены неравенствами. F = c1x1 + c2x2 → max (min)
x1 ≥ 0, x2 ≥ 0
Алгоритм графического способа решения задач линейного программирования заключается: 1) Построить прямые уравнения, которые получаются в результате замены в ограничения знаков неравенств на знаки равенств; 2) Найти полуплоскости, определяемые каждым из ограничений задачи; 3) Определить многоугольник решений; 4) Построить вектор 5) Построить прямую F = c1x1 + c2x2 = 0, проходящую через начало координат и перпендикулярную вектору 6) Передвигать прямую F в направлении вектора 7) Определить координаты точки экстремума функции и вычислить значение целевой функции в этой точки. Пример: Предприятие изготавливает два вида продукции – П1 и П2, которая поступает в оптовую продажу. Для производства продукции используются два вида сырья – А и В. Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице 5.
Таблица 5 - Расход сырья продукции
Опыт работы показал, что суточный спрос на продукцию П1 никогда не превышает спроса на продукцию П2 более чем на 1 ед. кроме того, известно, что спрос на продукцию П2 никогда не превышает 2 ед. в сутки. Оптовые цены единицы продукции равны: 3д.е. – для П1 4 д.е. для П2. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным? Решение: Для построения математической модели остается только идентифицировать переменные и представить цель и ограничения в виде математических функций этих переменных. Предположим, что предприятие изготовит х1 единиц продукции П1 и х2 единиц продукции П2. поскольку производство продукции П1 и П2 ограничено имеющимися в распоряжении в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию, а также учитывая, что количество изготавливаемых изделий не может быть отрицательным, должны выполняться следующие неравенства:
2х1 + 3х2 £ 9; 3х1 + 2х2 £ 13; х1 – х2 £ 1; х2 £ 2; х1 £ 0; х2 £ 0. Доход от реализации х1 единиц продукции П1 и х2 продукции П2 составит F = 3x1 + 4x2. Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение Fmax. Найдем решение данной задачи графическим способом. Построим многоугольник решений. Для этого в системе координат Х1 0 Х2 на плоскости изобразим граничные прямые:
2х1 + 3х2 = 9 (L1); 3х1 + 2х2 = 13 (L2); х1 – х2 = 1 (L3); х2 = 2 (L4).
Взяв какую-либо точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рисунке показаны стрелками. Областью решений являются многоугольник ОАВСD. Для построения прямой Z = 3х1 + 4х2 = 0 строим вектор-градиент
2х1 + 3х2 = 9; х1 – х2 = 1.
Оптимальный план задачи х1 = 2,4; х2 = 1,4. подставляя значения х1 и х2 в линейную функцию, получим:
Zmax = 3 * 2,4 + 4 * 1,4 = 12,8.
Полученное решение означает, что объем производства продукции П1 должен быть равен 2,4 ед., а продукции П2 – 1,4 ед. доход, получаемый в этом случае, составит: Z = 12,8 д.е.
Рисунок 5 – Геометрическая интерпретация решения задач линейного программирования
Свойства задач линейного программирования
При нахождении решения ЗЛП графическим способом могут встретиться следующие случаи (рисунки 6-9):
1
0 1 Fmin x F=0
Рисунок 6 – Единственное решение ЗЛП
A
1 x 0 1 Fmin
Рисунок 7 - Бесчисленное множество решений ЗЛП (любая точка отрезка АВ)
1
0 1 Fmin x F=0
Рисунок 8 – ЗЛП не имеет максимальное решение
y
1
0 1 x
Рисунок 9 – ЗЛП не имеет многоугольника решений
Задания для лабораторной работы 2 Задание №1 Построить математическую модель задачи линейного программирования, согласно номера своего варианта.
Вариант 1 Автотранспортному предприятию (АТП) необходимо освободить из-под груза складские помещения клиента. Вывоз груза следует осуществить в два рейса колоннами автомобилей. Условия перевозки требуют, чтобы в составе каждой колонны, предназначенной для вывоза груза в первый район, было 8 автомобилей ЗИЛ-131 и 8 автомобилей ЗИЛ-130; в колоннах второго рейса 8 автомобилей ЗИЛ-130 и 16 — МАЗ-500. Каждая из колонн может сделать за сутки одинаковое количество поездок. Парк подвижного состава АТП состоит из 32 автомобилей ЗИЛ-131 грузоподъемностью 3 т, 48 автомобилей ЗИЛ-130 грузоподъем-ностью 4 т, 48 автомобилей МАЗ-500 грузоподъемностью 7,5 т. Определите количество колонн, которое нужно направить в каждый район, чтобы перевезти наибольшее количество груза.
Вариант 2 Четыре овощехранилища каждый день обеспечивают картофелем три магазина. Магазины подали заявки соответственно на 17, 12 и 32 т. Овощехранилища имеют соответственно 20, 20, 15 и 25 т. Тарифы (в д.е. за 1 т) указаны в следующей таблице 6.
Таблица 6 – Условие задачи варианта 2
Составьте план перевозок, минимизирующий суммарные транспортные расходы.
Вариант 3 Имеются два склада готовой продукции: А1 и А2 с запаса- Составьте план перевозок, минимизирующий суммарные транспортные расходы.
Вариант 4 При откорме каждое животное должно получить не менее 9 ед. белков, 8 ед. углеводов и 11 ед. протеина. Для составления рациона используют два вида корма, представленных в следующей таблице 7.
Таблица 7 – Условие задачи варианта 4
Стоимость 1 кг корма первого вида - 4 д.е., второго - 6 д.е. Составьте дневной рацион питательности, имеющий минимальную стоимость.
Варианта 5 Хозяйство располагает следующими ресурсами: площадь 100 ед., труд - 120 ед., тяга - 80 ед. Хозяйство производит четыре вида продукции П1, П2, П3, П4. Организация производства харак- теризуется следующей таблицей 8.
Таблица 8 – Условие задачи варианта 5
Составьте план выпуска продукции, обеспечивающий хозяйству максимальную прибыль.
Вариант 6 Цех выпускает трансформаторы двух видов. Для изготовле- ния трансформаторов обоих видов используются железо и проволока. Общий запас железа - 3 т, проволоки - 18 т. На один трансформатор первого вида расходуются 5 кг железа и 3 кг проволоки, а на один трансформатор второго вида расходуются 3 кг железа и 2 кг проволоки. За каждый реализованный трансформатор первого вида завод получает прибыль 3 д. е., второго - 4 д. е. Составьте план выпуска трансформаторов, обеспечивающий заводу максимальную прибыль.
Вариант 7 Совхоз отвел три земельных массива размером 5000, 8000, 9000 га на посевы ржи, пшеницы, кукурузы. Средняя урожайность в центнерах на 1 га по массивам указана в следующей таблице 9.
Таблица 9 – Условие задачи варианта 7
За 1 ц ржи совхоз получает 2 д. е., за 1 ц пшеницы - 2,8 д. е., за I ц кукурузы — 1,4 д. е. Сколько гектаров и на каких массивах совхоз должен отвести на каждую культуру, чтобы получить максимальную выручку, если по плану он обязан сдать не менее 1900 т ржи, 158 000 т пшеницы и 30 000 т кукурузы?
Вариант 8 Из трех продуктов - I, II, III составляется смесь. В ее смеси должно входить не менее 6 ед. химического вещества А, 8 ед. вещества В и не менее 12 ед. вещества С. Структура химических веществ приведена в следующей таблице 10.
Таблица 10 – Условие задачи варианта 8
Составьте наиболее дешевую смесь.
Вариан 9 В институте проводится конкурс на лучшую стенгазету. Одному студенту дано следующее поручение: • купить акварельной краски по цене 30 д. е. за коробку, цветные карандаши по цене 20 д. е. за коробку, линейки по цене 12 д.е. блокноты по цене 10 д. е.; • красок нужно купить не менее трех коробок, блокнотов - столько, сколько коробок карандашей и красок вместе, линеек не более пяти. На покупки выделяется не менее 300 д. е. В каком количестве студент должен купить указанные предметы, чтобы общее число предметов было наибольшим?
Вариант 10 Цех выпускает три вида деталей - А, В, С. Каждая деталь обрабатывается тремя станками. Организация производства в цехе характеризуется следующей таблицей 11.
Таблица 11 – Условие задачи варианта 10
Составьте план загрузки станков, обеспечивающий цеху получение максимальной прибыли.
Вариант 11 Предприятие должно выпускать два вида продукции — А и В, используя при этом последовательно четыре станка. Данные о технологическом процессе указаны в следующей таблице 12.
Таблица 12 – Условие задачи варианта 11
Составьте план выпуска продукции, обеспечивающий предприятию наибольшую прибыль.
Вариант 12 На предприятии для производства запасных частей автомобилей используются три вида ресурсов. Выпускаются три вида запасных частей. Организация производства на предприятии характеризуется следующей таблицей 13.
Таблица 13 – Условие задачи варианта 12
Составьте план производства запасных частей, обеспечивающий предприятию максимальную прибыль.
Вариант 13 Нефтеперерабатывающий завод получает четыре полуфабриката: 400 тыс. л. алкилата, 250 тыс. л. крекинг-бензина, 350 тыс. л. бензина прямой перегонки и 100 тыс. л. изопентона. В результате смешивания этих четырех компонентов в разных пропорциях образуется три сорта авиационного бензина: бензин А-2:3:5:2, бензин В-3:1:2:1, бензин С-2:2:1:3. Стоимость 1 тыс. л. указанных сортов бензина характеризуется числами 120 д. е., 100 д. е., 150 д. е. Составьте план выпуска разных сортов авиационного бензина из условия получения максимальной стоимости всей продукции.
Вариант 14 Планируется нанесение удара по некоторому объекту тремя различными видами оружия: оружием А -в течение 3 мин., оружием Б - в течение 5 мин., оружием В - в течение 4 мин. Возможности средств обеспечения стрельбы таковы, что при применении оружия А в течение 3 мин., оружия Б в течение 2 мин., оружия В в течение 4 мин. общее количество залпов не должно превышать 15. При применении оружия А в течение 2 мин. и оружия В в течение 3 мин. общее количество залпов не должно превышать 8 ед. Кроме того, для преодоления противодействия противника необходимо, чтобы количество залпов оружием В за 1 мин. было больше, чем 5 ед. Рассчитайте темп стрельбы (количество залпов в 1 мин.) всеми
Вариант 15 Для участия в соревнованиях спортклуб должен выставить команду, состоящую из спортсменов I и II разрядов. Соревнования проводятся по бегу, прыжкам в высоту, прыжкам в длину. В беге должны участвовать 5 спортсменов, в прыжках в длину — 8 спортсменов, а в прыжках в высоту - не более 10. Количество очков, гарантируемых спортсмену каждого разряда по каждому виду, указано в следующей таблице 14.
Таблица 14 – Условие задачи варианта 15
Распределите спортсменов в команды так, чтобы сумма очков команды была наибольшей, если известно, что в команде I разряд имеют только 10 спортсменов.
Вариант 16 Звероферма выращивает черно-бурых лисиц и песцов. На звероферме имеется 10 000 клеток. В одной клетке могут быть Какое количество лисиц и песцов нужно держать на ферме чтобы получить наибольшую прибыль? Вариант 17 Имеются два элеватора, в которых сосредоточено ответственно 4200 и 1200 т зерна. Зерно необходимо перевезти трем хлебозаводам в количестве 1000, 2000 и 1600 т каждому. Расстояние от элеватора до хлебозаводов указано в следующей таблице 15.
Таблица 15 – Условие задачи варианта 17
Затраты на перевозку 1 т продукта на 1 км составляют 25 д.е. Спланируйте перевозки зерна из условия минимизации транспортных расходов.
Вариант 18 Из двух сортов бензина образуются две смеси — А и В. Составьте план образования смесей, при котором будет получен максимальный доход, если в наличии имеется бензина 50 т 1-го сорта и 30 т 2-го сорта.
Вариант 19 Имеются две почвенно-климатические зоны, площади которых соответственно равны 0,8 и 0,6 млн. га. Данные об урожайности зерновых культур приведены в следующей таблице 16.
Таблица 16 – Условие задачи варианта 19
Определите размеры посевных площадей озимых и яровых
Вариант 20 Для полива различных участков сада, на которых растут сливы, яблони, груши, служат три колодца. Колодцы могут дать соответственно 180, 90 и 40 ведер воды. Участки сада требуют для полива соответственно 100, 120 и 90 ведер воды. Расстояния (в метрах) от колодцев до участков сада указаны в следующей таблице 17.
Таблица 17 – Условие задачи варианта 20
Как лучше организовать полив?
Вариант 21 Предприятие производит сборку автомашин двух марок: А1 и А2. Для этого требуются следующие материалы: S1- комплекты заготовок металлоконструкций в количестве b1=17 шт., необходимые для сборки автомашин марок A1 и А2 (соответственно 2 и 3 ед.); S2 - комплекты резиновых изделий в количестве b2 = 11 шт. (соответственно 2 и 1 ед:); S3 -двигатели с арматурой и электрооборудованием в количестве b3 = 6 комплектов, необходимых по одному для каждой автомашины марки А1; S4 - двигатели с арматурой и электрооборудованием в количестве b4 = 5 комплектов, необходимых по одному для каждой автомашины марки А1 Стоимость автомашины марки A1 - с1 = 7 тыс. ден. ед., а автомашины А2 - с2 = 5 тыс. ден. ед. Определить план выпуска, обеспечивающий предприятию максимальную выручку.
Вариант 22 Для сохранения нормальной жизнедеятельности человек должен в сутки потреблять белков не менее 120 усл. ед., жиров не менее 70 и витаминов не менее 10 усл. ед. Содержание их в продуктах П1 и П2 равно соответственно (0,2; 0,075; 0) и (0,1; 0,1; 0,1). Стоимость 1 ед. продукта П1 - 2 ден. ед., П2 - 3 ден. ёд. Требуется так организовать питание, чтобы его стоимость была минимальной, а организм получил необходимое количество питательных веществ.
Вариант 23 Определить оптимальный план выпуска изделий с целью получения наибольшей прибыли от их реализации. Условия задачи приведены в таблице 18.
Таблица 18 – Условие задачи варианта 23
Вариант 24 Кондитерская фабрика на одной поточной линии может выпускать четыре вида шоколадных конфет. Определить план выпуска каждого сорта конфет и обеспечить наибольший экономический эффект. Данные приведены в таблице 19.
Таблица 19 – Условие задачи варианта 24
Вариант 25 Швейная фабрика выпускает мужские костюмы четырех артикулов. Составить план выпуска костюмов и минимизировать затраты на их изготовление по данным, приведенным в таблице 20.
Таблица 20 – Условие задачи варианта 25
Задание №2 Решить задачи линейного программирования графическим способом, согласно своего варианта. Во всех задачах x1 ≥ 0, х2 ≥ 0.
Вариант 1 Вариант 2 W = 2х1 - 5х2 → min; W = х1 - 4х2 → min;
2х1 + 3х2 ≤ 4 -3х1+ 10х2 ≤ 16
Вариант 3 Вариант 4 F = х1 + x2 → max; W = 2x1 + 2x2 → min;
2х1 + х2 ≤ 20 -x1 + x2 ≤ 1
Вариант 5 Вариант 6
х2 ≥ 3 - х1 + 2х2 ≤ 5 х1 + х2 ≤ 8
Вариант 7 Вариант 8 W = x1 - 3x2 → min; W = 2x1 + 5x1 → max;
x1 + 2x2 ≤ 5 x1 ≤ 400 x2 ≤ 300
Вариант 9 Вариант 10 W = x1 + 4x2 → max; W = 2x1 + x2 → max;
x1 ≤ 3 4x1 + 3x2 ≤ 11 x2 ≤ 1
Вариант 11 Вариант 12 W = 2x1 + 2x2 → min; W = 3x1 + 2x2 → max;
-x1 + 2x2 ≤ 8 x2 ≥ 0.6 0.1x1 + 0.4x2 ≤ 2
Вариант 13 Вариант 14 W = x1 + x2 → max; W = 5x1 + x2 → max;
2x1 + 3x2 ≤ 30 x1 ≤ 2.75 3x2 ≤ 1.1
Вариант 15 Вариант 16 W = 2x1 + 7x2 → max; W = x1 – 2x2 → min;
x2 ≥ 4 -2x1 + 24x2 ≤ 1 2x1 + 2x2 ≤ 9
Вариант 17 Вариант 18 W = x1 + 3x2 → max; W = 2x1 + 4x2 → max;
x1 ≤ 3 x1 + 6x2 ≤7 x2 ≤ 2
Вариант 19 Вариант 20 W = 2x1 + 3x2 → min; W = 4x1 + 6x2 → max;
-4x1 + 6x2 ≤ 2 x1 ≤ 31 x2 ≤ 2
Вариант 21 Вариант 22 W = 4x1 – x2 → min; W = 2x1 + x2 → min;
-5x1 + 8x2 ≤ 4 -2x1 + 9x2 ≤21
Вариант 23 Вариант 24 W = x1 + 5x2 → max; W = 2x1 + x2 → min;
x1 + 3x2 ≤ 7 -2x1 + 9x2 ≤ 21
Вариант 25 Вариант 26 W = x1 + 4x2 → max; W = 3x1 – 2x2 → min;
x2 ≥ 5 -3x1 + 8x2 ≤ 4 3x1 + x2 ≤ 16
2.5 Контрольные вопросы к защите лабораторной работы 2
1) Какие задачи относятся к задачам линейного программирования? 2) Что называется системой ограничения и целевой функцией задачи линейного программирования? 3) Что означает понятие каноническая форма запис
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 2172; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.70.0 (0.019 с.) |

 cjxj=c1x1+c2x2+…+cnxn → min (max) (2)
cjxj=c1x1+c2x2+…+cnxn → min (max) (2) aijxj ≤ bj (или ≥b), i =
aijxj ≤ bj (или ≥b), i =  = 1,2…m (3)
= 1,2…m (3) (4)
(4)
 (5)
(5)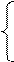 а1х1 + а2х2 ³ а
а1х1 + а2х2 ³ а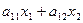 . Так как ресурса R1 должно хватить на выпуск товара Т1 и Т2, то затраты не должны превышать наличие этого ресурса, таким образом
. Так как ресурса R1 должно хватить на выпуск товара Т1 и Т2, то затраты не должны превышать наличие этого ресурса, таким образом  .
. (7)
(7) Таким образом, приходим к следующей задаче.
Таким образом, приходим к следующей задаче. x11 + x12 + x13 = a1,
x11 + x12 + x13 = a1, (9)
(9) = (c1;c2) – вектор градиент;
= (c1;c2) – вектор градиент;
 С = (3;4) и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направление вектора С. Из рисунка 9 следует, что по отношению к многоугольнику решений опорной эта прямая становится в точке С, где функция принимает максимальное значение. Точка С лежит на пересечении прямых L1 и L3. для определения ее координат решим систему уравнений:
С = (3;4) и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направление вектора С. Из рисунка 9 следует, что по отношению к многоугольнику решений опорной эта прямая становится в точке С, где функция принимает максимальное значение. Точка С лежит на пересечении прямых L1 и L3. для определения ее координат решим систему уравнений:


 y
y Fmax
Fmax y
y y
y



 F = 2x1 + 3х2 → max W = x1 – 3x2 → min;
F = 2x1 + 3х2 → max W = x1 – 3x2 → min;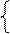 х1 ≥ 4 x1 + x2 ≤ 3
х1 ≥ 4 x1 + x2 ≤ 3
 -x1 + 2x2 ≤ 6 x1 + x2 ≤ 500
-x1 + 2x2 ≤ 6 x1 + x2 ≤ 500
 x1 + x2 ≤ 7 2x1 + 6x2 ≤ 15
x1 + x2 ≤ 7 2x1 + 6x2 ≤ 15
 x1 + x2 ≥ 4 x1 ≥ 1
x1 + x2 ≥ 4 x1 ≥ 1
 3x1 + x2 ≤ 20 3x1 + 6x2 ≤ 11
3x1 + x2 ≤ 20 3x1 + 6x2 ≤ 11 x1 ≥ 3 x1 + 10x2 ≤ 1
x1 ≥ 3 x1 + 10x2 ≤ 1
 4x1 + 8x2 ≤ 17 4x1 + x2 ≤ 15
4x1 + 8x2 ≤ 17 4x1 + x2 ≤ 15
 5x1 + 2x2 ≥ 3 x1 + 15x2 ≤ 32
5x1 + 2x2 ≥ 3 x1 + 15x2 ≤ 32