Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к лабораторной работе 2Содержание книги
Поиск на нашем сайте
3.3.1 Алгоритм симплекс-метода с помощью симплекс таблиц
Алгоритм симплекс-метода с помощью симплекс таблиц: 1) В последней строке симплекс таблице находят наименьший положительный элемент, не считая свободного члена. Столбец соответствующий этому элементу считается разрешающим; 2) Вычисляют отношения свободных членов к положительным элементам разрешающего столбца (симплекс отношение), находят наименьшее из этих симплекс отношений, оно соответствует разрешающей строке; 3) На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент;
Замечание: Если имеется несколько одинаковых по величине симплекс отношений, то выбирается любое из них, то же самое относится к положительным элементам последней строки симплекс таблице.
4) Далее переходят к следующей таблице, неизвестные переменные соответствуют разрешающей строке и столбцу меняются местами. При этом базисная переменная становится свободной переменной и наоборот. 5) Как только получается таблица, в которой в последней строке все элементы отрицательны, считается, что минимум найден. Минимальное значение функции равно свободному члену в строке целевой функции, а оптимальное решение определяется свободными членами при базисных переменных, все свободные переменные в этом случае равны нулю. 6) Если в разрешающем столбце все элементы отрицательны, то задача решений не имеет (минимум не достигается).
Замечание: Для того чтобы решать ЗЛП с помощью симплекс таблиц, необходимо её представить в канонической форме.
Пример: Найти минимум целевой функции F = x4 – x5 → min, если система ограничений имеет вид:
Решение: x4, x5 – свободные переменные x1, x2, x3 – базисные переменные (зависят от свободных)
Для составления симплекс-таблиц (таблицы 21-23) систему ограничений и функцию F необходимо представить в следующем виде:
F – x4 + x5 = 0
Таблица 21 – Первый шаг симплекс-метода
Таблица 22 – Второй шаг симплекс-метода
Таблица 23 – Третий шаг симплекс-метода
Ответ: Fmin = -
Задания для лабораторной работы 3 Согласно номеру своего варианта выбрать условие задачи из лабораторной работы №2 (любую одну задачу из двух). Решить задачу линейного программирования с использованием симплекс-таблиц.
3.5 Дополнительное задание Решите задачу линейного программирования симплекс-методом, согласно своего варианта:
x1 + х2 + 2х3 + 2х4 = 8; 2х1 + 2х2 +х3 +х4= 10; x1 — 2х2 + х3 + 2х4 = 1; xj ≥ 0; j = 1.4
2) max L = 2х1 + х2 + х3 + 2х4;
2х1 + x2 + 2х3 +х4 = 14; 2х1 + 2х2 - 2х3 + х4 = 4; xj ≥ 0; j = 1.4
3) min L = Зх1 + 2х2 + х3 + х4;
х2 + 2х3 + х4 = 4; x1 + 2х2 + 2х3 + 2х4 = 8; xj ≥ 0; j = 1.4
4) min L = 3x1 + 2х2 + х3 + 2х4;
х2 + 2х3 + х4 = 4; х1 + 2х2 + 2х3 + 2х4 = 8; xj ≥ 0; j = 1.4
5) max L = х1 + 2x2 + Зх3 + х4;
x1 + 2х2 + х3 + 2х4 = 8; 3x1 + Зх2 + х3 + Зх4 = 15; xj ≥ 0; j = 1.4
6) max L = 2x1 - x2 + 3x3 - 2x4;
2х1 + x2 - х3 + 2х4 = 4; х1 + 2х2 + х3 + х4 = 5; xj ≥ 0; j = 1.4
7) min L = 2x1 + x2 + 2x3 + 2x4;
x1 + x2 + x3 + 2x4 = 10; 2x1 + x2 + 2x3 + 2x4 = 10; xj ≥ 0; j = 1.4
x1 + x2 - x3 + x4 = 4; 2x1 + x2 + 2x3 - x4 = 4; x1 - x 2 + x3 + x4 = 2; xj ≥ 0; j = 1.4
9) min L = 4x1 + 2x2 + 2x3 +x4
2x1 + x2 + x3 + 2x4 = 10; x 1 + x2 + 2x3 - 2x4 = 6; xj ≥ 0; j = 1.4
x 1 + x2 - 2x3 + x4 = 2; x1 - 2x2 + x3 + 2x4 = 4; x 1 + 2x2 + 2x3 + 2x4 = 8; xj ≥ 0; j = 1.4
11) min L = x1 + 2x2 + 3x3 - x4;
x1 + 2x2 + x3 + 2x4 = 6; x 1 + 2x2 + 2x3 + x4 = 6; xj ≥ 0; j = 1.4
12) min L = x1 - 2x2 + 3x3 + x4;
x1 - 2x2 + x3 + 2x4 = 1; 3x 1 + x2 + 3x3 + 2x4 = 13; xj ≥ 0; j = 1.4
13) min L = 3x1 + x2 + 2x3 + x4;
2x1 + 2x3 + x4 = 7; x 1 + x2 + x3 + 2x4 = 7; xj ≥ 0; j = 1.4
14) min L = 2x1 + x2 + 3x3 + 2x4;
2x1 - 2x2 + x3 + x4 = 9; 2x 1 + 2x3 + x4 = 8; xj ≥ 0; j = 1.4
15) min L = 2x1 + x2 - x3 + 2x4;
x2 + x3 + 2x4 = 6; x 1 + 2x2 + 2x3 = 10; xj ≥ 0; j = 1.4
16) min L = x1 + 2x2 - x3 + 3x4;
x1 + x2 + 2x3 = 4; 2x2 + x3 = 4; xj ≥ 0; j = 1.4
17) min L = x1 + x2 - 2x3 + 2x4;
2x1 + x2 + x3 = 3; 2x 1 + x3 = 6; xj ≥ 0; j = 1.4
18) min L = x1 - 2x2 + 2x3 + 3x4;
x2 + 2x3 + x4 = 6; x 1 - 2x2 + x3 + x4 = 6; xj ≥ 0; j = 1.4
19) min L = -2x2 + x3;
x1 - x2 + x3 = 2; 2x 1 - x2 + 4x3 - x4 = 12; xj ≥ 0; j = 1.4
20) min L = 4x1 + 2x2 + 2x3 + x4;
2x1 + x2 + x3 + 2x4 = 10; x 1 + x2 + x3 - 2x4 = 6; xj ≥ 0; j = 1.4
21) min L = 4x1 + 3x2 + 2x3 + x4;
x1 - 2x2 + x3 + 2x4 = 4; x 1 + x3 = 1; xj ≥ 0; j = 1.4
22) min L = x1 + x2 + x3 + x4;
2x1 + 5x2 + 4x3 + x4 = 24; 3x 1 + 4x2 + 5x3 + x4 = 26; xj ≥ 0; j = 1.4
3x 1 + x3 + 2x4 = 2; -x1 + x2 + x3 + 5x4 = 5; xj ≥ 0; j = 1.4
24) min L = 2x1 - x2 + 3x3 - 5x4;
x2 + x3 + x4 = 9; x3 + x4 + x5 = 12; x4 + x5 + x6 = 15; xj ≥ 0; j = 1.6
25) min L = 2x1 - x2 + 3x3 - x4 + x5;
x1 + x2 + x4 = 1; x 1 + x2 + x5 = 2; xj ≥ 0; j = 1.5
3.6 Контрольные вопросы к защите лабораторной работы 3
1) В чем состоит практическая реализация симплекс – таблиц? 2) Какие переменные называются базисными переменными? 3) Какие переменные называются свободными переменными? 4) Как найти разрешающую строку, разрешающий столбец, разрешающий элемент в симплекс – таблице? 5) Как найти симплекс – отношение в симплекс – таблице? 6) В каком случае задача линейного программирования не имеет решения?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.223.221 (0.009 с.) |
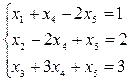
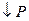
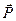
; x = (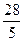
; 0; 0; 
; 
).
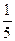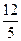1) max L = х1 - 2х2 + 2х3 + Зх4;
x1 + 2x2 +х3 + 2х4 = 16;
2х1 + Зх2 + Зх4 = 10;
x1 + x2 + 2х3 - х4 = 3;
2x1 + x2 + 2x3 + x4 = 8;
8) min L = x1 + 2x2 + x3 + x4;
10) min L = x1 + 2x2 + 3x3 + 4x4;
x 1 + x2 + 2x3 + x4 = 7;
x2 + 2x3 + 2x4 = 8;
x 1 + 2x3 + 2x4 = 5;
x 1 + x2 + 2x4 = 4;
x 1 + x2 + x3 + 2x4 = 8;
x 1 - 3x2 + x3 + x4 = 6;
3x 1 + 2x2 + 5x3 + x4 = 22;
23) min L = x1 - x2 + x3 - x4;
x 1 + x2 + x3 = 6;
-x 1 + x2 + x3 = 1;
