Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 1. Нахождение кратчайших путей в графеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математические методы МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ
Рекомендовано к изданию Редакционно-издательским советом государственного образовательного учреждения высшего профессионального образования «Оренбургский государственный университет»
Оренбург 2008 УДК 517(075.32) ББК 22.176 я 73 А - 92
Рецензент преподаватель кафедры вычислительной техники и математики КЭиБ ГОУ ОГУ Попова Л.А.
Атяскина Т.В. А-92 Математические методы [Текст]: методические указания к лабораторным работам. /Т.В.Атяскина. – Оренбург: ГОУ ОГУ, 2008. –40 с. Методические указания предназначены для выполнения лабораторных работ, обеспечивающих учебный процесс по дисциплине “Математические методы” в колледже электроники и бизнеса ОГУ для студентов 3 курса в 6 семестре специальности 230105 “программное обеспечение вычислительной техники и автоматизированных систем” очной формы обучения. Методические указания составлены с учетом Государственного образовательного стандарта среднего профессионального образования по направлению подготовки дипломированных специалистов - утвержденного 30.12.2003 Министерством Образования Российской Федерации. ББК 22.176 я 73
ã Атяскина Т.В., 2008
Содержание
Введение
По мере развития науки и техники перед человеком все чаще встает проблема: «Как найти правильное решение?». Для облегчения решения этой задачи реальные процессы (или объекты) заменяются их аналогами или моделями. Затем производится анализ поведения модели в тех или иных условиях с помощью персонального компьютера. В этом случае говорят о компьютерном моделировании. Но персональный компьютер может работать только с математическими моделями, которые с помощью языков программирования переводятся в набор машинных кодов, которые и обрабатывает персональный компьютер. Какое же место занимают математические модели и как они получаются? Построение математической модели процесса, явления или объекта начинается с построения упрощенного варианта модели, в котором учитываются только основные черты. В результате прослеживаются основные связи между входными параметрами, ограничениями и показателем эффективности. Общего подхода к построению модели нет. В каждом конкретном случае при построении математической модели учитывается большое количество факторов: цель построения модели, круг решаемых задач, точность описания модели и точность выполнения вычислений. Математическая модель должна отражать все существенные факторы, определяющие ее поведение, и при этом быть простой и удобной для восприятия результатов. Каждая математическая модель процесса, явления или объекта в своей основе имеет математический количественный метод. Применение математических количественных методов для обоснования выбора того или иного управляющего решения во всех областях человеческой деятельности называется исследованием операций. Целью исследования операций является нахождение с использованием специального математического аппарата решения, удовлетворяющего заданным условиям.
Содержание отчета Отчет по лабораторной работе должен содержать: 1) тему работы; 2) цель работы; 3) ход работы; 4) постановку задачи, с указанием предметной области; 5) модель задачи; 6) аналитическое решение задачи алгоритмами Краскала и Прима; 7) распечатку программы решения задачи; 8) результаты решения задачи.
Понятие графа
Графом G=(X,U) называется пара двух конечных множеств: Х – множество точек (вершин) и U – множество линий (ребер), соединяющих некоторые пары точек. Если граф имеет ребро, у которого начало и конец совпадают, то это ребро называется петлей. Если ребро графа имеет направление, то оно называется дугой.
1.3.2 Виды графов
Существуют следующие виды графов: 1) Граф, состоящий из вершин и соединяющих их ребер, называется неориентированным (н-граф); 2) Граф, состоящий из вершин и соединяющих их дуг, называется ориентированным (орграф); 3) Ребра, соединяющие одну и ту же пару вершин, называются параллельными или кратными. Граф, содержащий кратные ребра называется мультиграфом; 4) Граф, в котором проведены все возможные ребра, но не имеющий петель и кратных ребер, называется полным; 5) Граф, содержащий как ребра, так и дуги называется смешанным;
1.3.3 Матричное представление графа
Матрицей смежности графа G - называется квадратная матрица порядка n, где n – число вершин графа G и определяется следующим образом:
Аnxn=[аij] = 1 – есть ребро (дуга) (хi; хj) или петля;
0 – нет ребра (дуги) (хi; хj).
Матрицей ициденции графа G с n вершинами и m дугами называется матрица
Вnxm=[bij] = -1, если хi – конец дуги (хi; xj), 0, если нет дуги (хi; xj).
В матрицу инциденции н-графа заносят 1, если ребро инцидентно соответствующей вершине, 0 – в противном случае.
Путь – это упорядоченная последовательность ребер ориентированного графа, в которой конец предыдущего ребра совпадает с началом следующего и все ребра единственны.
Матрицей достижимости графа G называется квадратная матрица порядка n, где n – число вершин графа и определяется следующим образом:
1, если есть путь из хi в xj, Dnxn=[dij] = 0, если нет пути из хi в xj.
Граф не содержащий циклов называется ациклическим. Связанный ациклический граф называется деревом. Н-граф называется неориентированным деревом, если он связан и не содержит циклов, а значит петель и кратных рёбер. Дерево – это минимально связный граф, в том смысле, что при удалении хотя бы одного ребра он теряет связность.
Теорема: В дереве с n вершинами всегда n-1 ребро.
Ориентированным деревом или ордеревом, или корневым деревом называют орграф со следующими свойствами: 1) Существует единый узел, полустепень захода которого равна нулю, он называется корнем дерева; 2) Полустепень захода всех остальных узлов равна единице; 3) Каждый узел достижим из корня.
Остовом графа называется подграф являющийся деревом. Если граф полный, то в графе существует
1.3.4 Алгоритм Краскала
1) Строится нуль-граф (одни вершины без ребер). 2) Упорядочиваются ребра графа в порядке не убывания их весов. 3) Выбираются из упорядоченного списка ребра, такие чтобы они не образовывали цикл в графе. 4) Если выбрано n-1 ребро (n – число вершин графа), то алгоритм заканчивает работу. 5) Остов должен включать в себя все вершины графа.
Пример: Найти кратчайший остов в графе (рисунок 1) алгоритмом Краскала. X1 2 X2
X6 4 4 3 X3 44 4 1 1 X5 6 X4
Рисунок 1 – Взвешенный граф
Решение:
1) Построим таблицу ребер данного графа, в порядке неубывания их весов (таблица 1).
Таблица 1 – Список ребер графа в порядке неубывания весов
2) Из таблицы 1 выбираем ребра, которые не образуют цикл в графе и строим кратчайший остов (рисунок 2).
X1 X2
X6 X3
Х5 X4
Рисунок 2 – Кратчайший остов графа
3) Вычислим длину кратчайшего остова: d = 1+1+2+3+3 = 10
Для реализации алгоритма Краскала на ПК необходимо: 1) Построить матрицу смежности исходного графа; 2) Составить список ребер с их весами и отсортировать их одним из способов сортировки. Для того чтобы уменьшить время сортировки можно сортировать не весь список, а N-1 ребро, с минимальным весом; 3) Для проверки на цикл можно использовать построение матрицы достижимости после каждого добавления ребра. Добавляем ребро XiXj, смотрим есть ли единица в матрице достижимости на месте XiXj, если есть, то ребро XiXj не перебрасываем в матрицу смежности исходного остова, так как получаем цикл, если единицы нет, то ребро XiXj заносим в матрицу смежности остова.
1.3.5 Алгоритм Прима Данный алгоритм определяет кратчайший остов в графе. Суть данного метода заключается в том, что построение кратчайшего остова выполняется путем добавления к строящемуся остову некоторой ближайшей к нему вершины и соответствующего ребра. Обозначения: Ts – множество вершин строящегося остова As – множество ребер строящегося остова
Для вершины Х1 делаем пометку Х1*. Выписываем связи всех остальных вершин с помеченной вершиной: [помеченная вершина; вес] – если связь есть или [0;¥] – если связи нет. Среди имеющихся связей выбираем вершину, которая имеет с помеченной вершиной наименьшее соединение. Такую вершину добавляем к множеству Ts, а соответствующее ребро к множеству As. Алгоритм заканчивает свою работу, если n=N(Ts), где n – количество вершин графа, N(Ts) – количество вершин остова.
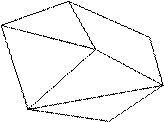
Пример: Найти кратчайший остов в графе (рисунок 3) алгоритмом Прима.
Х1 7 6 Х3 8 Х5 6 11 5 3 7 Х4 Х6 4 2 Х7
Рисунок 3 – Граф с весами
Решение: 1) Выписываем связи вершин графа с помеченной вершиной: X1*: X2*: X3*: x2-[x1; 2]-min x3-[x2; 6]-min x4-[x3; 6]-min x3-[0, ¥] x4-[0, ¥] x5-[0, ¥] x4-[0,¥] x5-[x2; 7] x6-[0, ¥] x5-[x1; 8] x6-[0, ¥] x7-[0, ¥] x6-[x1; 11] x7-[0, ¥] x7-[0,¥]
X4*: X7*: X6*: x5[x4; 5] x5[0, ¥] x5[x6; 3]-min x6[x4; 7] x6[x7; 2]-min x7[x4; 4]-min
Ts = {x1, x2, x3, x4, x7, x6, x5} As = { (x1;x2), (x2;x3),(x3;x4),(x4;x7),(x7;x6),(x6;x5)}
2) Используя найденные множества Ts и As, построим кратчайший остов данного графа (рисунок 4).
Х2
Х1 Х3
Х5 Х4 Х6 Х7
Рисунок 4 – Кратчайший остов графа
3) Найдем длину получившегося остова: d = 2+6+6+4+2+3 = 23
Задание для лабораторной работы 1 Составить постановку задачи, выбрав предметную область (составить граф не менее чем из 8 вершин). Решить задачу алгоритмами Краскала и Прима аналитически; Составить программу решения задачи в среде программирования Delphi (Реализация одного алгоритма - оценка «3» или «4»; реализация двух алгоритмов – оценка «5»);
1.5 Контрольные вопросы к защите лабораторной работы 1
1) Что называется графом? Приведите пример. 2) Какие графы называются ориентированными? Какие графы – неориентированные? 3) Какой граф называется взвешенным? 4) Что называется матрицей смежности, матрицей инциденции, матрицей достижимости. 5) Что называется полным графом? Какая закономерность между вершинами и ребрами в полном графе? 6) Что называется деревом? Приведите пример. 7) Что называется остовом? Приведите пример. 8) Какое количество остовов в полном графе? 9) Что называется кратчайшим остовом? 10) Что называется циклом в графе? 11) Алгоритм Краскала. 12) Алгоритм Прима.
Задания для лабораторной работы 2 Задание №1 Построить математическую модель задачи линейного программирования, согласно номера своего варианта.
Вариант 1 Автотранспортному предприятию (АТП) необходимо освободить из-под груза складские помещения клиента. Вывоз груза следует осуществить в два рейса колоннами автомобилей. Условия перевозки требуют, чтобы в составе каждой колонны, предназначенной для вывоза груза в первый район, было 8 автомобилей ЗИЛ-131 и 8 автомобилей ЗИЛ-130; в колоннах второго рейса 8 автомобилей ЗИЛ-130 и 16 — МАЗ-500. Каждая из колонн может сделать за сутки одинаковое количество поездок. Парк подвижного состава АТП состоит из 32 автомобилей ЗИЛ-131 грузоподъемностью 3 т, 48 автомобилей ЗИЛ-130 грузоподъем-ностью 4 т, 48 автомобилей МАЗ-500 грузоподъемностью 7,5 т. Определите количество колонн, которое нужно направить в каждый район, чтобы перевезти наибольшее количество груза.
Вариант 2 Четыре овощехранилища каждый день обеспечивают картофелем три магазина. Магазины подали заявки соответственно на 17, 12 и 32 т. Овощехранилища имеют соответственно 20, 20, 15 и 25 т. Тарифы (в д.е. за 1 т) указаны в следующей таблице 6.
Таблица 6 – Условие задачи варианта 2
Составьте план перевозок, минимизирующий суммарные транспортные расходы.
Вариант 3 Имеются два склада готовой продукции: А1 и А2 с запаса- Составьте план перевозок, минимизирующий суммарные транспортные расходы.
Вариант 4 При откорме каждое животное должно получить не менее 9 ед. белков, 8 ед. углеводов и 11 ед. протеина. Для составления рациона используют два вида корма, представленных в следующей таблице 7.
Таблица 7 – Условие задачи варианта 4
Стоимость 1 кг корма первого вида - 4 д.е., второго - 6 д.е. Составьте дневной рацион питательности, имеющий минимальную стоимость.
Варианта 5 Хозяйство располагает следующими ресурсами: площадь 100 ед., труд - 120 ед., тяга - 80 ед. Хозяйство производит четыре вида продукции П1, П2, П3, П4. Организация производства харак- теризуется следующей таблицей 8.
Таблица 8 – Условие задачи варианта 5
Составьте план выпуска продукции, обеспечивающий хозяйству максимальную прибыль.
Вариант 6 Цех выпускает трансформаторы двух видов. Для изготовле- ния трансформаторов обоих видов используются железо и проволока. Общий запас железа - 3 т, проволоки - 18 т. На один трансформатор первого вида расходуются 5 кг железа и 3 кг проволоки, а на один трансформатор второго вида расходуются 3 кг железа и 2 кг проволоки. За каждый реализованный трансформатор первого вида завод получает прибыль 3 д. е., второго - 4 д. е. Составьте план выпуска трансформаторов, обеспечивающий заводу максимальную прибыль.
Вариант 7 Совхоз отвел три земельных массива размером 5000, 8000, 9000 га на посевы ржи, пшеницы, кукурузы. Средняя урожайность в центнерах на 1 га по массивам указана в следующей таблице 9.
Таблица 9 – Условие задачи варианта 7
За 1 ц ржи совхоз получает 2 д. е., за 1 ц пшеницы - 2,8 д. е., за I ц кукурузы — 1,4 д. е. Сколько гектаров и на каких массивах совхоз должен отвести на каждую культуру, чтобы получить максимальную выручку, если по плану он обязан сдать не менее 1900 т ржи, 158 000 т пшеницы и 30 000 т кукурузы?
Вариант 8 Из трех продуктов - I, II, III составляется смесь. В ее смеси должно входить не менее 6 ед. химического вещества А, 8 ед. вещества В и не менее 12 ед. вещества С. Структура химических веществ приведена в следующей таблице 10.
Таблица 10 – Условие задачи варианта 8
Составьте наиболее дешевую смесь.
Вариан 9 В институте проводится конкурс на лучшую стенгазету. Одному студенту дано следующее поручение: • купить акварельной краски по цене 30 д. е. за коробку, цветные карандаши по цене 20 д. е. за коробку, линейки по цене 12 д.е. блокноты по цене 10 д. е.; • красок нужно купить не менее трех коробок, блокнотов - столько, сколько коробок карандашей и красок вместе, линеек не более пяти. На покупки выделяется не менее 300 д. е. В каком количестве студент должен купить указанные предметы, чтобы общее число предметов было наибольшим?
Вариант 10 Цех выпускает три вида деталей - А, В, С. Каждая деталь обрабатывается тремя станками. Организация производства в цехе характеризуется следующей таблицей 11.
Таблица 11 – Условие задачи варианта 10
Составьте план загрузки станков, обеспечивающий цеху получение максимальной прибыли.
Вариант 11 Предприятие должно выпускать два вида продукции — А и В, используя при этом последовательно четыре станка. Данные о технологическом процессе указаны в следующей таблице 12.
Таблица 12 – Условие задачи варианта 11
Составьте план выпуска продукции, обеспечивающий предприятию наибольшую прибыль.
Вариант 12 На предприятии для производства запасных частей автомобилей используются три вида ресурсов. Выпускаются три вида запасных частей. Организация производства на предприятии характеризуется следующей таблицей 13.
Таблица 13 – Условие задачи варианта 12
Составьте план производства запасных частей, обеспечивающий предприятию максимальную прибыль.
Вариант 13 Нефтеперерабатывающий завод получает четыре полуфабриката: 400 тыс. л. алкилата, 250 тыс. л. крекинг-бензина, 350 тыс. л. бензина прямой перегонки и 100 тыс. л. изопентона. В результате смешивания этих четырех компонентов в разных пропорциях образуется три сорта авиационного бензина: бензин А-2:3:5:2, бензин В-3:1:2:1, бензин С-2:2:1:3. Стоимость 1 тыс. л. указанных сортов бензина характеризуется числами 120 д. е., 100 д. е., 150 д. е. Составьте план выпуска разных сортов авиационного бензина из условия получения максимальной стоимости всей продукции.
Вариант 14 Планируется нанесение удара по некоторому объекту тремя различными видами оружия: оружием А -в течение 3 мин., оружием Б - в течение 5 мин., оружием В - в течение 4 мин. Возможности средств обеспечения стрельбы таковы, что при применении оружия А в течение 3 мин., оружия Б в течение 2 мин., оружия В в течение 4 мин. общее количество залпов не должно превышать 15. При применении оружия А в течение 2 мин. и оружия В в течение 3 мин. общее количество залпов не должно превышать 8 ед. Кроме того, для преодоления противодействия противника необходимо, чтобы количество залпов оружием В за 1 мин. было больше, чем 5 ед. Рассчитайте темп стрельбы (количество залпов в 1 мин.) всеми
Вариант 15 Для участия в соревнованиях спортклуб должен выставить команду, состоящую из спортсменов I и II разрядов. Соревнования проводятся по бегу, прыжкам в высоту, прыжкам в длину. В беге должны участвовать 5 спортсменов, в прыжках в длину — 8 спортсменов, а в прыжках в высоту - не более 10. Количество очков, гарантируемых спортсмену каждого разряда по каждому виду, указано в следующей таблице 14.
Таблица 14 – Условие задачи варианта 15
Распределите спортсменов в команды так, чтобы сумма очков команды была наибольшей, если известно, что в команде I разряд имеют только 10 спортсменов.
Вариант 16 Звероферма выращивает черно-бурых лисиц и песцов. На звероферме имеется 10 000 клеток. В одной клетке могут быть Какое количество лисиц и песцов нужно держать на ферме чтобы получить наибольшую прибыль? Вариант 17 Имеются два элеватора, в которых сосредоточено ответственно 4200 и 1200 т зерна. Зерно необходимо перевезти трем хлебозаводам в количестве 1000, 2000 и 1600 т каждому. Расстояние от элеватора до хлебозаводов указано в следующей таблице 15.
Таблица 15 – Условие задачи варианта 17
Затраты на перевозку 1 т продукта на 1 км составляют 25 д.е. Спланируйте перевозки зерна из условия минимизации транспортных расходов.
Вариант 18 Из двух сортов бензина образуются две смеси — А и В. Составьте план образования смесей, при котором будет получен максимальный доход, если в наличии имеется бензина 50 т 1-го сорта и 30 т 2-го сорта.
Вариант 19 Имеются две почвенно-климатические зоны, площади которых соответственно равны 0,8 и 0,6 млн. га. Данные об урожайности зерновых культур приведены в следующей таблице 16.
Таблица 16 – Условие задачи варианта 19
Определите размеры посевных площадей озимых и яровых
Вариант 20 Для полива различных участков сада, на которых растут сливы, яблони, груши, служат три колодца. Колодцы могут дать соответственно 180, 90 и 40 ведер воды. Участки сада требуют для полива соответственно 100, 120 и 90 ведер воды. Расстояния (в метрах) от колодцев до участков сада указаны в следующей таблице 17.
Таблица 17 – Условие задачи варианта 20
Как лучше организовать полив?
Вариант 21 Предприятие производит сборку автомашин двух марок: А1 и А2. Для этого требуются следующие материалы: S1- комплекты заготовок металлоконструкций в количестве b1=17 шт., необходимые для сборки автомашин марок A1 и А2 (соответственно 2 и 3 ед.); S2 - комплекты резиновых изделий в количестве b2 = 11 шт. (соответственно 2 и 1 ед:); S3 -двигатели с арматурой и электрооборудованием в количестве b3 = 6 комплектов, необходимых по одному для каждой автомашины марки А1; S4 - двигатели с арматурой и электрооборудованием в количестве b4 = 5 комплектов, необходимых по одному для каждой автомашины марки А1 Стоимость автомашины марки A1 - с1 = 7 тыс. ден. ед., а автомашины А2 - с2 = 5 тыс. ден. ед. Определить план выпуска, обеспечивающий предприятию максимальную выручку.
Вариант 22 Для сохранения нормальной жизнедеятельности человек должен в сутки потреблять белков не менее 120 усл. ед., жиров не менее 70 и витаминов не менее 10 усл. ед. Содержание их в продуктах П1 и П2 равно соответственно (0,2; 0,075; 0) и (0,1; 0,1; 0,1). Стоимость 1 ед. продукта П1 - 2 ден. ед., П2 - 3 ден. ёд. Требуется так организовать питание, чтобы его стоимость была минимальной, а организм получил необходимое количество питательных веществ.
Вариант 23 Определить оптимальный план выпуска изделий с целью получения наибольшей прибыли от их реализации. Условия задачи приведены в таблице 18.
Таблица 18 – Условие задачи варианта 23
Вариант 24 Кондитерская фабрика на одной поточной линии может выпускать четыре вида шоколадных конфет. Определить план выпуска каждого сорта конфет и обеспечить наибольший экономический эффект. Данные приведены в таблице 19.
Таблица 19 – Условие задачи варианта 24
Вариант 25 Швейная фабрика выпускает мужские костюмы четырех артикулов. Составить план выпуска костюмов и минимизировать затраты на их изготовление по данным, приведенным в таблице 20.
Таблица 20 – Условие задачи варианта 25
Задание №2 Решить задачи линейного программирования графическим способом, согласно своего варианта. Во всех задачах x1 ≥ 0, х2 ≥ 0.
Вариант 1 Вариант 2 W = 2х1 - 5х2 → min; W = х1 - 4х2 → min;
2х1 + 3х2 ≤ 4 -3х1+ 10х2 ≤ 16
Вариант 3 Вариант 4 F = х1 + x2 → max; W = 2x1 + 2x2 → min;
2х1 + х2 ≤ 20 -x1 + x2 ≤ 1
Вариант 5 Вариант 6
х2 ≥ 3 - х1 + 2х2 ≤ 5 х1 + х2 ≤ 8
Вариант 7 Вариант 8 W = x1 - 3x2 → min; W = 2x1 + 5x1 → max;
x1 + 2x2 ≤ 5 x1 ≤ 400 x2 ≤ 300
Вариант 9 Вариант 10 W = x1 + 4x2 → max; W = 2x1 + x2 → max;
x1 ≤ 3 4x1 + 3x2 ≤ 11 x2 ≤ 1
Вариант 11 Вариант 12 W = 2x1 + 2x2 → min; W = 3x1 + 2x2 → max;
-x1 + 2x2 ≤ 8 x2 ≥ 0.6 0.1x1 + 0.4x2 ≤ 2
Вариант 13 Вариант 14 W = x1 + x2 → max; W = 5x1 + x2 → max;
2x1 + 3x2 ≤ 30 x1 ≤ 2.75 3x2 ≤ 1.1
Вариант 15 Вариант 16 W = 2x1 + 7x2 → max; W = x1 – 2x2 → min;
x2 ≥ 4 -2x1 + 24x2 ≤ 1 2x1 + 2x2 ≤ 9
Вариант 17 Вариант 18 W = x1 + 3x2 → max; W = 2x1 + 4x2 → max;
x1 ≤ 3 x1 + 6x2 ≤7 x2 ≤ 2
Вариант 19 Вариант 20 W = 2x1 + 3x2 → min; W = 4x1 + 6x2 → max;
-4x1 + 6x2 ≤ 2 x1 ≤ 31 x2 ≤ 2
Вариант 21 Вариант 22 W = 4x1 – x2 → min; W = 2x1 + x2 → min;
-5x1 + 8x2 ≤ 4 -2x1 + 9x2 ≤21
Вариант 23 Вариант 24 W = x1 + 5x2 → max; W = 2x1 + x2 → min;
x1 + 3x2 ≤ 7 -2x1 + 9x2 ≤ 21
Вариант 25 Вариант 26 W = x1 + 4x2 → max; W = 3x1 – 2x2 → min;
x2 ≥ 5 -3x1 + 8x2 ≤ 4 3x1 + x2 ≤ 16
2.5 Контрольные вопросы к защите лабораторной работы 2
1) Какие задачи относятся к задачам линейного программирования? 2) Что называется системой ограничения и целевой функцией задачи линейного программирования? 3) Что означает понятие каноническая форма записи задачи линейного 4) Какое решение называется оптимальным? 5) Как определяется область допустимых решений? 6) Что означает понятие вектор решений (вектор-градиент)? 7) В каком случае задача линейного программирования не имеет решение? Содержание отчета Отчет по лабораторной работе должен содержать: 1) тему работы; 2) цель работы; 3) ход работы; 4) формулировку задания; 5) решение задачи своего варианта с использованием симплекс-таблиц.
Задания для лабораторной работы 3 Согласно номеру своего варианта выбрать условие задачи из лабораторной работы №2 (любую одну задачу из двух). Решить задачу линейного программирования с использованием симплекс-таблиц.
3.5 Дополнительное задание Решите задачу линейного программирования симплекс-мет
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1010; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.20.233.113 (0.019 с.) |

 ã ГОУ ОГУ, 2008
ã ГОУ ОГУ, 2008
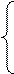 1, если хi – начало дуги (хi; xj), или петля,
1, если хi – начало дуги (хi; xj), или петля,
 остовов, где n – число вершин графа.
остовов, где n – число вершин графа. 3 5
3 5
 2 Х2
2 Х2


 F = 2x1 + 3х2 → max W = x1 – 3x2 → min;
F = 2x1 + 3х2 → max W = x1 – 3x2 → min; х1 ≥ 4 x1 + x2 ≤ 3
х1 ≥ 4 x1 + x2 ≤ 3
 -x1 + 2x2 ≤ 6 x1 + x2 ≤ 500
-x1 + 2x2 ≤ 6 x1 + x2 ≤ 500
 x1 + x2 ≤ 7 2x1 + 6x2 ≤ 15
x1 + x2 ≤ 7 2x1 + 6x2 ≤ 15
 x1 + x2 ≥ 4 x1 ≥ 1
x1 + x2 ≥ 4 x1 ≥ 1
 3x1 + x2 ≤ 20 3x1 + 6x2 ≤ 11
3x1 + x2 ≤ 20 3x1 + 6x2 ≤ 11 x1 ≥ 3 x1 + 10x2 ≤ 1
x1 ≥ 3 x1 + 10x2 ≤ 1
 4x1 + 8x2 ≤ 17 4x1 + x2 ≤ 15
4x1 + 8x2 ≤ 17 4x1 + x2 ≤ 15
 5x1 + 2x2 ≥ 3 x1 + 15x2 ≤ 32
5x1 + 2x2 ≥ 3 x1 + 15x2 ≤ 32