Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 3-18 определение числа Авогадро с помощьюСодержание книги
Поиск на нашем сайте
РЕНТГЕНОСТРУКТУРНОГО ИЗМЕРЕНИЯ ПОСТОЯННОЙ КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ
Цель работы:определить постоянную кристаллической решетки ичисло Авогадро, используя рентгенограмму, снятую по методу Дебая – Шерера.
Принадлежности:рентгенограмма,снятая в K Cu- излучении(= 1,537 Å) от медного образца (= 8600 кг/м, = 64 кг/моль, кристаллическая решетка гранецентрированная).
Теоретическое введение
Явление дифракции рентгеновских лучей на кристаллических решет-ках широко используют для анализа структуры твердых тел.
Наибольшее распространение получил метод Дебая – Шерера, в ко-тором в качестве образца используется мелкокристаллический порошок исследуемого материала. Такое вещество даже в сравнительно малом (до 1 мм3) объеме содержит огромное число кристалликов, расположенных беспорядочно относительно друг друга.
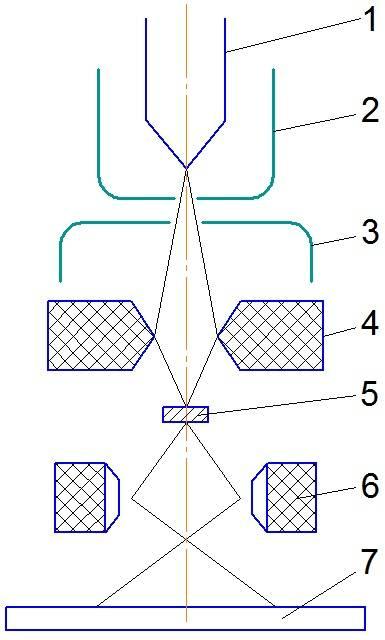
Если через такой образец 1 (рис. 18.1) пропустить пучок монохрома-тических рентгеновских лучей 2, то для любой заданной кристаллографи-ческой плоскости 3 с индексами Миллера h, k, l найдутся кристаллики, ориентированные так, что эта плоскость образует с падающим рентгенов-ским пучком угол, удовлетворяющий условию главных дифракционных максимумов Вульфа – Брегга
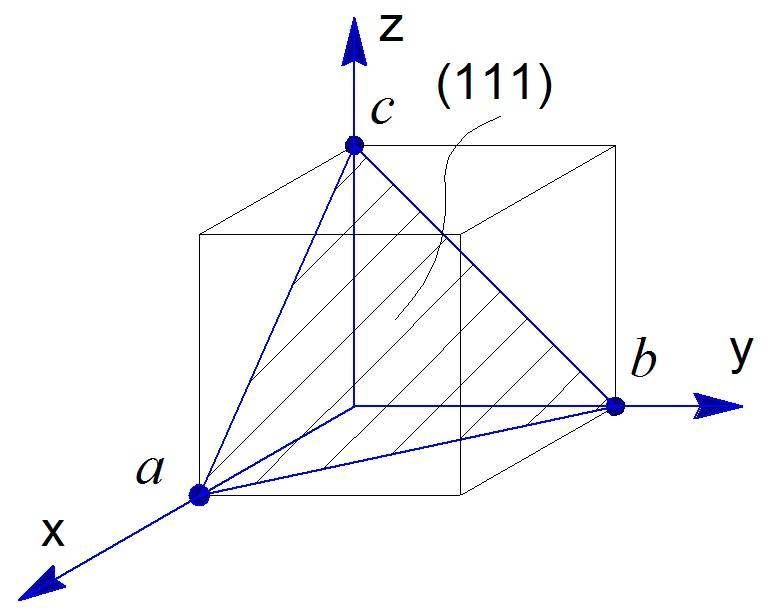
где dhkl – межплоскостное расстояние; – длина волны рентгеновского из-лучения. Целые числа h, k, l, называемые индексами Миллера, использу-ют для определения положения кристаллографической плоскости в кри-сталлической решетке. Если оси координат направить вдоль ребер эле-ментарной ячейки, то значения индексов Миллера будут обратны величи-нам отрезков, отсекаемых кристаллографической плоскостью на осях ко-ординат (рис. 18.2). Штриховкой на рисунке показана плоскость (111).
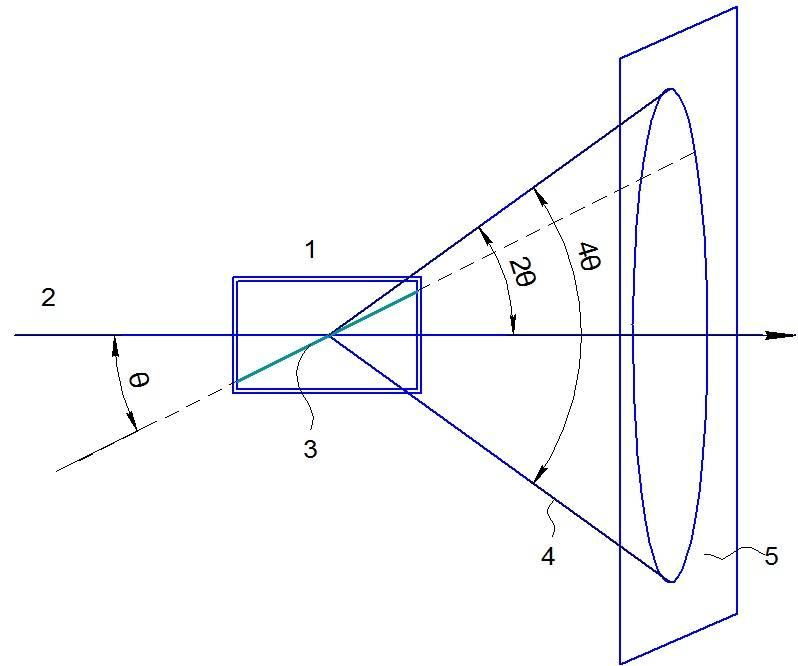
Лучи, отраженные от таких кристаллографических плоскостей, обра-зуют дифракционные максимумы в направлении, составляющем угол 2 с падающим лучом. Отраженные лучи будут образовывать поверхность ко-нуса 4 (см. рис. 18.1) с углом раствора в 4, ось которого совпадает с направлением падающего пучка 2.
Если на пути лучей расположить плоскую фотопленку 5, то отражен-ные лучи оставят на ней след в виде концентрических колец.
Рис. 18.1
Рис. 18.2
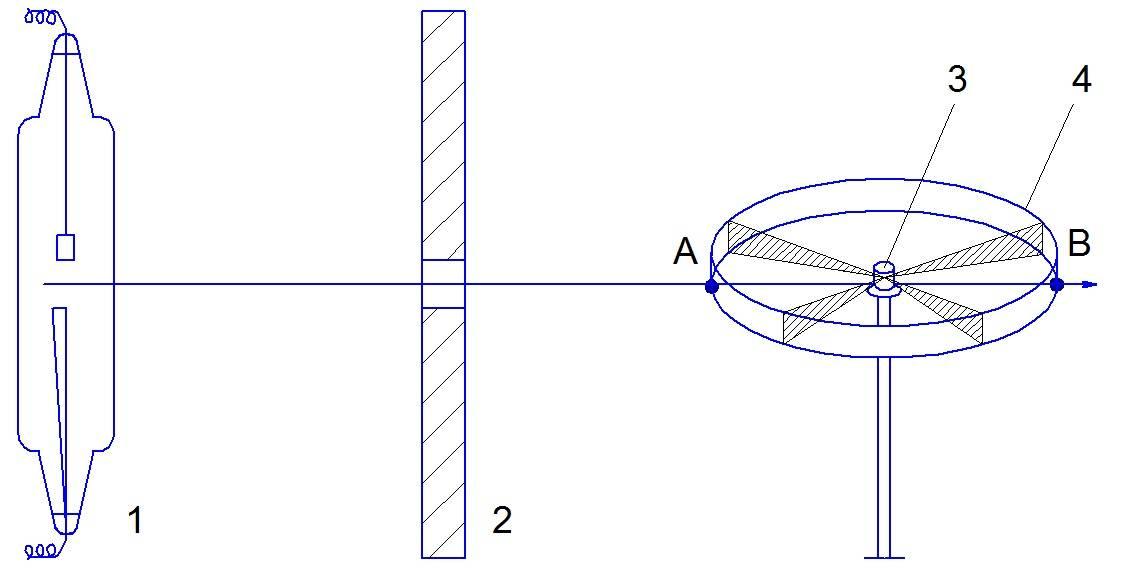
На рис. 18.3 представлена схема установки для рентгеноструктурно-го анализа методом Дебая – Шерера. Источником рентгеновского излуче-ния является рентгеновская трубка 1 (с медным антикатодом в данном случае). Из потока рентгеновского излучения с помощью свинцовой диа-фрагмы 2 вырезается тонкий пучок, направленный на образец 3. Образец
окружен цилиндрической фотопленкой 4. А и В – точки входа и выхода рент-геновского пучка соответственно.
Рис. 18.3
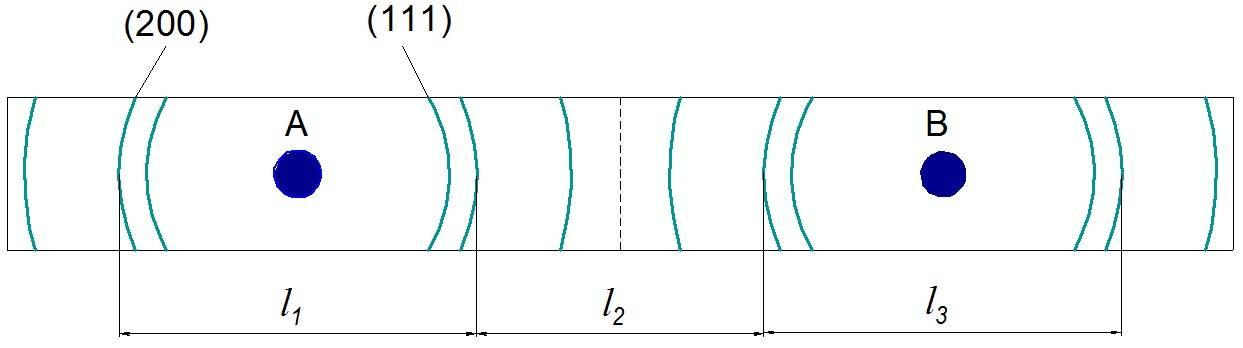
На рис. 18.4 изображен общий вид рентгенограммы, полученной на этой установке. Если же образец окружить цилиндрической узкой фотопленкой, то следы отраженных лучей будут иметь вид дуг кривых, образующихся при пересечении конуса с этим цилиндром. А и В – точки входа и выхода рентгеновского пучка; l1, l2, l3 – расстояния между симметричными линиями (дифракционными максимумами от кристаллографических плоскостей с одинаковыми индексами Миллера h, k, l).
Рис. 18.4
После снятия рентгенограммы необходимо ее расшифровать, т. е. определить индексы плоскостей, соответствующих данным дифракционным максимумам, и рассчитать постоянные a, b, c решетки кристалла.
В общем случае для решеток с малой симметрией (триклинная, моноклинная системы) эта задача представляет большие трудности. Проще всего она решается для кристаллов кубической системы, где периоды кристаллической решетки равны: а = b = c. Межплоскостное расстояние в этом случае определяется выражением
2 asin а период кристаллической решетки
2 sin
Рассчитать углы соответствующих дифракционных линий можно, определив радиус цилиндра R, образованного фотопленкой, и измерив расстояние между симметричными линиями. Как видно из рис. 18.3 и 18.4, длина окружности цилиндра, образованного фотопленкой, L = l1+2l2+l3. Следовательно, радиус цилиндра
Поскольку угол скольжения мал, то
Подставив выражение (18.3) в (18.2), получим формулу для опреде-ления постоянной кристаллической решетки
Авогадро: m
NA
При подсчете числа атомов, приходящихся на одну элементарную ячейку, необходимо учитывать, что атомы, расположенные в вершинах куба, одновременно принадлежат восьми элементарным ячейкам, а рас-положенные в центрах граней – двум. Поэтому для простой кубической решетки n = 1, а для гранецентрированной – n = 4.
Метод определения числа Авогадро по значению постоянной кри-сталлической решетки является наиболее точным из современных мето-дов.
Порядок выполнения работы
1. На данной рентгенограмме, полученной для медного образца, из-мерить расстояния l1, l2, l3 для групп максимумов от кристаллографиче-ских плоскостей (111), (200).
2. Вычислить постоянную решетки меди для этих двух случаев по формуле (18.4) и определить ее среднее значение.
3. По формуле (18.5) рассчитать число Авогадро. 4. Проанализировать полученные результаты. Сделать выводы.
Контрольные вопросы
Вариант 1
1. Опишите механизм образования рентгеновских лучей в рентге-новской трубке. 2. Объясните, почему не наблюдается дифракции видимого света на кристаллических решетках.
3. Приведите примеры использования рентгеновского излучения в науке и технике помимо рентгеноструктурного анализа.
4. Задача. На грань кристалла падает параллельный пучок рентге-
новских лучей с длиной волны = 1,47 Å. Расстояние между атомными плос-костями кристалла d = 2,8 Å. Под каким углом скольжения наблюдается ди-фракционный максимум второго порядка?
Ответ: arcsin m 31040.2 d
Вариант 2
1. В чем отличие тормозного рентгеновского излучения от характе-ристического? Нарисуйте спектр тормозного рентгеновского излучения. 2. Выведите формулу Вульфа – Брегга.
3. Приведите примеры использования рентгеновского излучения в аэрокосмической области. 4. Задача. Узкий пучок рентгеновских лучей падает на монокристаллNaCl. Наименьший угол скольжения, при котором еще наблюдается зер-кальное отражение от системы кристаллографических плоскостей с меж-
плоскостным расстоянием d = 2,8 Å, равен 40 6. Найти напряжение на рентге-новской трубке.
2 desin
Лабораторная работа № 3-19
ИСПОЛЬЗОВАНИЕ ЭЛЕКТРОНОГРАММ ДЛЯ ОПРЕДЕЛЕНИЯ ПОСТОЯННЫХ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК
Цель работы:ознакомиться с методом электронографического ис-следования структуры твердых тел (металлов), используя электронограм-мы, определить постоянные кристаллических решеток серебра и меди.
Приборы и принадлежности:электронограммы тонких поликри-сталлических пленок Al, Aq, Cu.
Теоретическое введение
1. Особенности электронографического анализа структуры ве-щества.
Явление дифракции электронов на кристаллических решетках твер-дых тел имеет очень важное значение в современной науке и технике уже хотя бы потому, что именно в этом явлении впервые были обнаружены волновые свойства микрочастиц. Оно хотя и сходно в «кинетическом» от-ношении с эффектом дифракции рентгеновских лучей, однако имеет ряд особенностей, которые определяют область применения электроногра-фии. К ним прежде всего относятся:
а) сильное взаимодействие электронов с веществом; б) малая длина их волны.
Сильное взаимодействие электронов с электрическими полями атом-ных ядер и электронных оболочек атомов приводит к тому, что метод ди-фракции электронов используется для изучения структуры молекул, тон-ких пленок и поверхностных слоев.
Малая длина волны электронов дает возможность получения ди-фракционной картины со сравнительно тонкими линиями (дифракционны-ми максимумами) от объекта, линейные размеры которого порядка не-скольких межатомных расстояний; рентгенограмма таких объектов обна-руживает весьма размытую «диффузионную» дифракционную картину. Это имеет особое значение при изучении аморфных и жидких веществ.
Отрицательной стороной малости длин волн является смещение всей дифракционной картины в область малых углов. Поэтому при иссле-довании веществ, имеющих сложную кристаллическую решетку, на элек-тронограмме может наблюдаться наложение линий, что затрудняет рас-чет кристаллической структуры.
2. Аппаратура для электронографических исследований. Электронографические исследования требуют более сложного тех-ники эксперимента по сравнению с рентгеновскими исследованиями.
Очень малая длина свободного пробега электронов в воздухе требу-ет, чтобы получение и регистрация картины рассеяния происходили в ва-кууме 10-1 – 10- 3 Па, в связи с чем электронографические исследования производятся в специальных приборах – электронографах, где создается требуемый вакуум.
Конструкция простейшего электронографа представлена на рис. 19.1. Источником электронов является вольфрамовый термокатод 1. Генерируемый им поток электронов фокусируется электродом 2 в тонкий пучок и ускоряется анодом 3 (разность потенциалов между катодом и анодом составляет 10…100 кВ). Фокусирующая система 4 конденсирует изображение электронного пучка на исследуемый образец 5. Результат дифракции электронов после прохождения через образец с помощью набора электромагнитных линз 6 проецируется на катодолюминисцентный экран 7 (вместо экрана может использоваться фотопластинка). Нужно от-метить, что вид электронограмм может принимать различные формы и
определяется структурой образца.
3. Расчет простейших электронограмм.
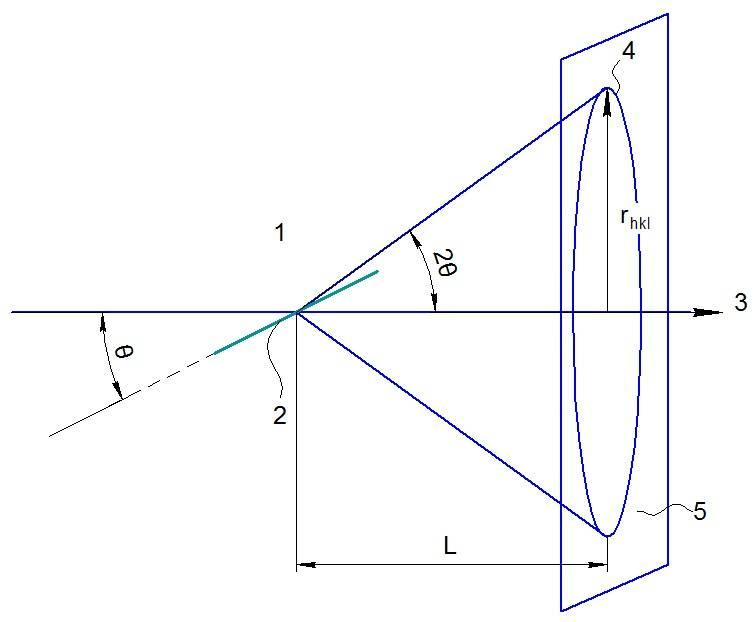
Типичная электронограмма от поликристаллического образца представляет собой набор концентрических колец. На рис.
2 – кристаллографическая плоскость; 3 – направление первичного пучка электронов; 4 – дифракционное кольцо на экране 5. Определение параметров кристаллической решетки по электронограмме осуществляется на основании уравнения Вульфа – Брегга
где d – расстояние между кристаллографическими плоскостями,
проведенными через узлы кристаллической решетки; – угол скольжения лучей; – длина волны электронов в падающем пучке; m – порядок
дифракционного максимума (в данной лабораторной работе равен единице).
Рис. 19.2
Межплоскостное расстояние d в общем случае является функцией величин ребер элементарной ячейки a, в, с (см. рис. 18.2). Так, в случае простейшей кубической решетки постоянная кристаллической решетки
где h, k, l – индексы Миллера(см. описание лабораторной работы 3-18). Так как угол скольжения для быстрых электронов мал (рис. 19.2), то его можно определить из соотношения rhkl tq 2 2, L т.е. rhkl , (19.3) 2 L
где L – расстояние от образца до экрана (фотопленки); rhkl – радиус дифракционного кольца на экране (фотопластинке), соответствующего отражению от кристаллографической плоскости с индексами (h, k, l).
Подставив (19.3) в уравнение (19.1), получим выражение для межплоскостного расстояния
Таким образом, из уравнений (19.2) и (19.4) следует, что для кубических кристаллов постоянную решетки можно найти по формуле
rhkl Как видно из этой формулы, для определения постоянной решетки необходимо знать постоянную электронографа L (произведение длины волны на расстояние от образца до экрана). Самым распространенным и надежным способом определения величины L является применение «стандартных» образцов. В качестве «стандартного» образца в данной работе используется тонкая пленка алюминия, постоянная решетки которого точно известна.
Длину волны электрона, ускоренного разностью потенциалов U, можно найти с помощью уравнения де Бройля:
где h – постоянная Планка; m – масса электрона; – скорость электрона.
Поскольку работа сил электрического поля идет на сообщение электрону кинетической энергии eU m 2,
то скорость электрона
2 eU . m
Подставив скорость электрона в уравнение де Бройля (19.6), получим
Эта формула может быть приведена к более удобной форме:
(если U подставить в вольтах, то получится в ангстремах).
Порядок выполнения работы
1. С помощью электронограммы тонкой пленки Al (постоянная кристаллической решетки Al а = 4,05 Å) по формуле (19.5) рассчитать постоянную электронографа L для линий (111), (200), (220), (311) и найти её среднее значение.
2. Зная, что ускоряющее напряжение при съемке электронограмм в электронографе было U = 60 кВ, по формуле (19.7) определить длину волны электронов. Зная постоянную электронографа L и длину волны электронов, определить расстояние L от образца до фотопленки в электронографе.
3. С помощью электронограммы тонкой пленки Aq (зная постоянную электронографа L) вычислить по формуле (19.5) постоянную кристаллической решетки Aq для линий (111), (200), (220), (311) и найти ее среднее значение.
4. То же самое выполнить для электронограммы тонкой пленки Си.
Контрольные вопросы
Вариант 1
1. Какое свойство электронов используется в электронографии для анализа структуры твердого тела? 2. Запишите уравнение де Бройля. Каков его физический смысл? 3. Приведите примеры использования волновых свойств микрочастиц (кроме электронографии) в науке и технике.
4. Задача. Параллельный пучок моноэнергетичных электроновпадает по нормали на диафрагму с узкой прямоугольной щелью шириной b = 1мкм.Определить скорость электронов,если на экране,которыйнаходится на расстоянии L = 50 см от щели, ширина центрального
дифракционного максимума х = 0,36 мм.
1. В чем заключается корпускулярно-волновой дуализм вещества?
2. Какие виды электронных микроскопов Вы знаете? Каковы общие принципы их работы?
3. Каковы особенности взаимодействия электронов с веществом по сравнению с электромагнитным излучением? Как это используется в электронной микроскопии?
4. Задача. Какую ускоряющую разность потенциалов U долженпройти пучок электронов, чтобы при отражении от монокристалла никеля
с постоянной решетки d = 0,352 нм при угле скольжения = 50 наблюдался максимум интенсивности отраженного пучка первого порядка? h 2 Ответ : U 8 med 4 sin 2 400 В.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.116 (0.008 с.) |

 Тогда уравнение Вульфа – Брегга (18.1) для m = 1 примет вид
Тогда уравнение Вульфа – Брегга (18.1) для m = 1 примет вид
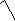
 h 2 k 2 l 2,
h 2 k 2 l 2, a
a