Методические указания к лабораторной работе 1

 

Понятие графа

 

Графом G=(X,U) называется пара двух конечных множеств: Х – множество точек (вершин) и U – множество линий (ребер), соединяющих некоторые пары точек.

Если граф имеет ребро, у которого начало и конец совпадают, то это ребро называется петлей.

Если ребро графа имеет направление, то оно называется дугой.

 

1.3.2 Виды графов

 

Существуют следующие виды графов:

1) Граф, состоящий из вершин и соединяющих их ребер, называется неориентированным (н-граф);

2) Граф, состоящий из вершин и соединяющих их дуг, называется ориентированным (орграф);

3) Ребра, соединяющие одну и ту же пару вершин, называются параллельными или кратными. Граф, содержащий кратные ребра называется мультиграфом;

4) Граф, в котором проведены все возможные ребра, но не имеющий петель и кратных ребер, называется полным;

5) Граф, содержащий как ребра, так и дуги называется смешанным;

 

1.3.3 Матричное представление графа

 

Матрицей смежности графа G - называется квадратная матрица порядка n, где n – число вершин графа G и определяется следующим образом:

А_nxn=[а_ij] = 1 – есть ребро (дуга) (х_i; х_j) или петля;

 

0 – нет ребра (дуги) (х_i; х_j).

 

Матрицей ициденции графа G с n вершинами и m дугами называется матрица

1, если х_i – начало дуги (х_i; x_j), или петля,

В_nxm=[b_ij] = -1, если х_i – конец дуги (х_i; x_j),

0, если нет дуги (х_i; x_j).

 

В матрицу инциденции н-графа заносят 1, если ребро инцидентно соответствующей вершине, 0 – в противном случае.

 

Путь – это упорядоченная последовательность ребер ориентированного графа, в которой конец предыдущего ребра совпадает с началом следующего и все ребра единственны.

 

Матрицей достижимости графа G называется квадратная матрица порядка n, где n – число вершин графа и определяется следующим образом:

1, если есть путь из х_i в x_j,

D_nxn=[d_ij] =

0, если нет пути из х_i в x_j.

 

Граф не содержащий циклов называется ациклическим.

Связанный ациклический граф называется деревом.

Н-граф называется неориентированным деревом, если он связан и не содержит циклов, а значит петель и кратных рёбер.

Дерево – это минимально связный граф, в том смысле, что при удалении хотя бы одного ребра он теряет связность.

 

Теорема: В дереве с n вершинами всегда n-1 ребро.

 

Ориентированным деревом или ордеревом, или корневым деревом называют орграф со следующими свойствами:

1) Существует единый узел, полустепень захода которого равна нулю, он называется корнем дерева;

2) Полустепень захода всех остальных узлов равна единице;

3) Каждый узел достижим из корня.

 

Остовом графа называется подграф являющийся деревом.

Если граф полный, то в графе существует остовов, где n – число вершин графа.

 

1.3.4 Алгоритм Краскала

 

1) Строится нуль-граф (одни вершины без ребер).

2) Упорядочиваются ребра графа в порядке не убывания их весов.

3) Выбираются из упорядоченного списка ребра, такие чтобы они не образовывали цикл в графе.

4) Если выбрано n-1 ребро (n – число вершин графа), то алгоритм заканчивает работу.

5) Остов должен включать в себя все вершины графа.

 

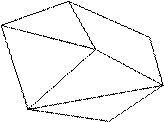
Пример: Найти кратчайший остов в графе (рисунок 1) алгоритмом Краскала.

X1 2 X2

3 5

X6 4 4 3 X3

44 4

1 1

X5 6 X4

 

Рисунок 1 – Взвешенный граф

 

Решение:

 

1) Построим таблицу ребер данного графа, в порядке неубывания их весов (таблица 1).

 

 

Таблица 1 – Список ребер графа в порядке неубывания весов

 

Начало	Конец	Вес
Х5 Х3 Х1 Х1 Х2	Х6 Х4 Х2 Х6 Х4
Х1 Х1 Х2 Х4	Х4 Х5 Х3 Х5

 

2) Из таблицы 1 выбираем ребра, которые не образуют цикл в графе и строим кратчайший остов (рисунок 2).

 

 

X1 X2

X6 X3

 

Х5 X4

 

Рисунок 2 – Кратчайший остов графа

 

3) Вычислим длину кратчайшего остова: d = 1+1+2+3+3 = 10

 

Для реализации алгоритма Краскала на ПК необходимо:

1) Построить матрицу смежности исходного графа;

2) Составить список ребер с их весами и отсортировать их одним из способов сортировки. Для того чтобы уменьшить время сортировки можно сортировать не весь список, а N-1 ребро, с минимальным весом;

3) Для проверки на цикл можно использовать построение матрицы достижимости после каждого добавления ребра. Добавляем ребро XiXj, смотрим есть ли единица в матрице достижимости на месте XiXj, если есть, то ребро XiXj не перебрасываем в матрицу смежности исходного остова, так как получаем цикл, если единицы нет, то ребро XiXj заносим в матрицу смежности остова.

 

 

1.3.5 Алгоритм Прима

Данный алгоритм определяет кратчайший остов в графе.

Суть данного метода заключается в том, что построение кратчайшего остова выполняется путем добавления к строящемуся остову некоторой ближайшей к нему вершины и соответствующего ребра.

Обозначения:

Ts – множество вершин строящегося остова

As – множество ребер строящегося остова

 

Для вершины Х₁ делаем пометку Х₁^*. Выписываем связи всех остальных вершин с помеченной вершиной: [помеченная вершина; вес] – если связь есть или [0;¥] – если связи нет. Среди имеющихся связей выбираем вершину, которая имеет с помеченной вершиной наименьшее соединение. Такую вершину добавляем к множеству Ts, а соответствующее ребро к множеству As. Алгоритм заканчивает свою работу, если n=N(Ts), где n – количество вершин графа, N(Ts) – количество вершин остова.

 

Пример: Найти кратчайший остов в графе (рисунок 3) алгоритмом Прима.

 

2 Х2

Х1 7 6 Х3

8 Х5 6

11 5

3 7 Х4

Х6 4

2 Х7

 

Рисунок 3 – Граф с весами

 

Решение:

1) Выписываем связи вершин графа с помеченной вершиной:

X1*: X2*: X3*:

x2-[x1; 2]-min x3-[x2; 6]-min x4-[x3; 6]-min

x3-[0, ¥] x4-[0, ¥] x5-[0, ¥]

x4-[0,¥] x5-[x2; 7] x6-[0, ¥]

x5-[x1; 8] x6-[0, ¥] x7-[0, ¥]

x6-[x1; 11] x7-[0, ¥]

x7-[0,¥]

 

 

X4*: X7*: X6*:

x5[x4; 5] x5[0, ¥] x5[x6; 3]-min

x6[x4; 7] x6[x7; 2]-min

x7[x4; 4]-min

 

Ts = {x1, x2, x3, x4, x7, x6, x5}

As = { (x1;x2), (x2;x3),(x3;x4),(x4;x7),(x7;x6),(x6;x5)}

 

2) Используя найденные множества Ts и As, построим кратчайший остов данного графа (рисунок 4).

 

Х2

Х1 Х3

 

Х5

Х4

Х6

Х7

 

Рисунок 4 – Кратчайший остов графа

 

3) Найдем длину получившегося остова: d = 2+6+6+4+2+3 = 23

 

Задание для лабораторной работы 1

Составить постановку задачи, выбрав предметную область (составить граф не менее чем из 8 вершин). Решить задачу алгоритмами Краскала и Прима аналитически;

Составить программу решения задачи в среде программирования Delphi (Реализация одного алгоритма - оценка «3» или «4»; реализация двух алгоритмов – оценка «5»);

 

1.5 Контрольные вопросы к защите лабораторной работы 1

 

1) Что называется графом? Приведите пример.

2) Какие графы называются ориентированными? Какие графы – неориентированные?

3) Какой граф называется взвешенным?

4) Что называется матрицей смежности, матрицей инциденции, матрицей достижимости.

5) Что называется полным графом? Какая закономерность между вершинами и ребрами в полном графе?

6) Что называется деревом? Приведите пример.

7) Что называется остовом? Приведите пример.

8) Какое количество остовов в полном графе?

9) Что называется кратчайшим остовом?

10) Что называется циклом в графе?

11) Алгоритм Краскала.

12) Алгоритм Прима.