
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочная совокупность. Метод моментов. Интервальные оценки параметров генеральной совокупности. Доверительная вероятность.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пример 2.1. Дана выборка объема n=10:
Оценить с надежностью 0,95 математическое ожидание а нормально распределенного признака по выборочной средней при помощи доверительного интервала. Решение: вычислим по определению выборочную среднюю
DВ = Пользуясь таблицей приложения 3 по g = 0,95 и n = 10, находим tg=2,26, тогда искомый доверительный интервал Ответ:
Пример 2.2. Дано статистическое распределение выборки: в первой строке указаны выборочные варианты х i, а во второй строке – соответственные частоты n i количественного признака Х). Требуется найти доверительный интервал для оценки неизвестного математического ожидания а с заданной надежностью g=0,95.
Решение: 1. Для нахождения
Вычислим условные моменты: Теперь, зная ложный ноль С=280 и шаг выборки h=270 – 260 =10, вычисляем выборочную среднюю: 2. Доверительный интервал. DВ=160 Þ s= Пользуясь таблицей приложения 3 по g = 0,95 и n = 100 находим tg=1,984, тогда искомый доверительный интервал Ответ: 1. а)
Задачи для самостоятельного решения: 1) Дано статистическое распределение выборки: в первой строке указаны выборочные варианты х i, а во второй строке – соответственные частоты n i количественного признака Х). Требуется найти: 1. Методом произведений: а) выборочную среднюю; б) выборочное среднее квадратическое отклонение; 2. Доверительные интервалы для оценки неизвестного математического ожидания а нормально распределенной случайной величины Х с заданной надежностью g=0,95.
1.1)
1.2)
1.3)
1.4)
1.5)
1.6)
1.7)
1.8)
1.9)
1.10)
Проверка статистических гипотез. Проверка гипотез о значении математического ожидания Статистическая гипотеза. Нулевая гипотеза. Конкурирующая гипотеза. Критическая область: левосторонняя, правосторонняя, двусторонняя. Критерий согласия. Критерии проверки гипотез о значении математического ожидания. Пример 3.1. Пример 1. Фирма утверждает, что средний срок безотказной работы изделия 2900ч. Для выборки из 50 изделий средний срок равен 2720 ч. При выбор средн кв отклонения 700ч. При 5% уровне значимости проверить гипотезу о том, что 2900 ч – математических ожиданий Решение. Критерий
Пример 3.2. Фирма предлагает автоматы по разливу напитков. При выборе n=16 найдено Решение.
Задачи для самостоятельного решения: 1. Проверить гипотезу о значении математического ожидания значению
1.1)
1.2)
2. По данным двух выборок проверить гипотезу о равенстве математических ожиданий;
2.1)
2.2)
3. Фирма-поставщик в рекламном буклете утверждает, что средний срок безотказной работы предлагаемого изделия – 2900 ч. Для выборки из 50 изделий средний срок безотказной работы оказался равным 2720 ч при среднем квадратическом отклонении 700 ч. При 5-% уровне значимости проверить гипотезу о том, что значение 2900 ч является математическим ожиданием.
4. Составлена выборка из 64 покупателей, которые интересовались товаром А. Из них товар А купили 16 человек. Поставщик утверждает, что данный товар должен привлечь треть покупателей, а среднее квадратическое отклонение равно одному человеку. Проверить нулевую гипотезу при 5-% уровне значимости.
5. Средний диаметр подшипников должен составлять 35 мм. Однако для выборки из 82 подшипников он составил 35,3 мм при выборочном среднем квадратическом отклонении 0,1 мм. При 5-% уровне значимости проверить гипотезу о том, что станок, на котором изготавливают подшипники, не требует подналадки.
6. По результатам 10 замеров установлено, что среднее время обслуживания мастером клиента равно 15 мин. Предполагая, что время обслуживания – нормально распределенная случайная величина, с дисперсией
7. Из большой партии ананасов одного размера извлечена выборка из 36 штук. Выборочная средняя масса одной штуки при этом оказалось равна 930 г. Используя двусторонний критерий проверить гипотезу о том, что средняя масса одного ананаса составляет 1 кг., если: А) среднее квадратическое отклонение известно и составляет 200 г.; Б) среднее квадратическое отклонениенеизвестно, а выборочное составляет 250 г.
8. Фирма продает автоматы по розливу напитков. По выборке из n=16 средняя величина дозы, наливаемой в стакан первым автоматом – 182 г.По выборке m=9 средняя величина величина дозы, наливаемой в стакан вторым автоматом – 185 г. По утверждению изготовителя, случайная величина наливаемой дозы имеет нормальное распределение с дисперсией 25 г. Можно ли считать отличия выборочных средних случайной ошибкой при уровне значимости 0,01?
9. На двух станках производят одну и туже продукцию, контролируемую по наружному диаметру изделия. Из продукции станка А было проверено 16 изделий, а из продукции станка В – 25 изделий. Выборочные оценки математических ожиданий и дисперсий контролируемых размеров составили
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.249.61 (0.011 с.) |

 =
=  (-2×2 + 1×1 + 2×2 + 3×2 + 4×2 + 5×1) = 2;
(-2×2 + 1×1 + 2×2 + 3×2 + 4×2 + 5×1) = 2; =
=  - 22 =
- 22 =  » 2,4.
» 2,4. примет вид:
примет вид: 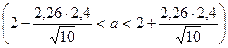 , т.е.
, т.е.  .
. и DВ методом произведений составим расчетную таблицу (в качестве ложного нуля выбираем С=280, т.е. u3=0, значит, u2= -1, u1= -2, u4=1, u 5 = 2, u6 = 3, u7 = 4):
и DВ методом произведений составим расчетную таблицу (в качестве ложного нуля выбираем С=280, т.е. u3=0, значит, u2= -1, u1= -2, u4=1, u 5 = 2, u6 = 3, u7 = 4):

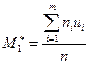 =
=  =0,4;
=0,4;  =
=  =1,76.
=1,76. =10×0,4+280=284; выборочную дисперсию:
=10×0,4+280=284; выборочную дисперсию:  = (1,76 – 0,42)×102 = 160; выборочное среднее квадратическое отклонение: sВ =
= (1,76 – 0,42)×102 = 160; выборочное среднее квадратическое отклонение: sВ =  =
=  »12,65.
»12,65. =
=  » 12,71.
» 12,71. , т.е.
, т.е. 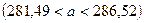 .
.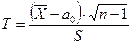 - случайная величина, имеющая распределение Стьюдента.
- случайная величина, имеющая распределение Стьюдента.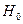 :
: 
 :
: 
 <2900
<2900
 - левосторонняя критическая точка
- левосторонняя критическая точка =>
=>  отвергается
отвергается г дозы в стакане автоматом №1. По выборке m=9 найдена
г дозы в стакане автоматом №1. По выборке m=9 найдена  г дозы, наливаемой в стакан автоматом №2. По утверждению изготовить сл/в наливаемой дозы имеет нормальный знач распределения с
г дозы, наливаемой в стакан автоматом №2. По утверждению изготовить сл/в наливаемой дозы имеет нормальный знач распределения с 
 . Можно ли считать, что автомат №2 наливает в стакан большую дозу напитка.
. Можно ли считать, что автомат №2 наливает в стакан большую дозу напитка.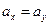 ;
;  ;
;  ;
; 
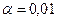 ;
; 
 =>
=> 
 => принимается
=> принимается 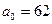
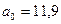
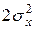 =9 при уровне значимости 0,05 установить, можно ли принять в качестве норматива для обслуживания одного клиента 21 мин?
=9 при уровне значимости 0,05 установить, можно ли принять в качестве норматива для обслуживания одного клиента 21 мин? , sA2=1,21, sB2=1,44. Проверить гипотезу о равенстве математических ожиданий при α=0.1.
, sA2=1,21, sB2=1,44. Проверить гипотезу о равенстве математических ожиданий при α=0.1.


