Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дати визначення реляційної моделі даних і назвати її складові елементи; пояснити роботу операцій реляційної алгебри.Содержание книги
Поиск на нашем сайте Реляційна модель даних – модель, при якій дані представляються і вигляді таблиць (relations). Характерною рисою є наявність високорівневої мови для пошуку та визначення даних. Реляційні об’єкти даних: домен, таблиці, індекси. Домен – поіменована множина атомарних значень синтаксично і семантично однорідних. Домен описує тип даних і діапазон значень, що може приймати атрибут і повинен відноситися до деякого базового типу. Індекс — об'єкт бд, що створений з ціллю підвищення ефективності виконання запитів. Індекс формується зі значень одного чи кількох стовпчиків таблиці і вказівників на відповідні рядки таблиці і, таким чином, дозволяє знаходити потрібний рядок по заданому значенню. Прискорення роботи з використанням індексів досягається в першу чергу за рахунок того, що індекс має структуру, що оптимізована для пошуку - наприклад, збалансованого дерева. Реляційна модель передбачає представлення даних у вигляді двомірних таблиць.
• структурної частини • Цілісної частини • Маніпуляційна частини Структурна частина описує, які об'єкти розглядаються реляційної моделлю.Відношення виступає в якості ждиної структури. Цілісна частина – використовує механізм, який дозволяє звязувати відношення між собою. Цілісність підтримується за рахунок цілісності відношень та за рухунок звязків між відношеннями. Це цілісність сутностей і цілісність зовнішніх ключів. Маніпуляційна частина описує два еквівалентних способу маніпулювання реляційними даними - реляційних алгебри та реляційні обчислення доменів, кортежів. Реляційна алгебра: А={U, D, dom, R, r, o}, де U- множина атрибутів, D-множина доменів, dom-функція з Uв D, R-множина всіх схем над атрибутами U, r-множина всіх відношень зі схемою R, o-множина реляційних операцій. В реляційній алгебрі, в якості об’єктів розгладаються відношення, а якості операцій-реляційні операції. Реляційна алгебра - формальна система маніпулювання відносинами в реляційної моделі даних. Мінімальний набір операцій: декартовий добуток, об’єднання, різниця, проекція, селекція. Додаткові операції: перетин, тета-з’єднання, природні з’єднання, частка. Булеві операції:до блевих відносяться наступні теоретико-множинні операції: Об’єднання виконується над відношеннями, що мають однакову схему і включає всі кортежі (рядки), які належать хоча б одному з даних відношень. Рядки не дублюються. Ri U r2= {ti / (ti є r1) V (ti є r2)} Перетин – результатом є відношення, яке включає ті кортежі, які належать одночасно двом відношенням. Ri ∩ r2= {ti / (ti є r1) ^ (ti єr2)} Різниця. Повертає відношення, яке включає всі кортежі, які належать першому, і не належать другому. Ri \ r2= {ti / (ti є r1)^ (ti не є r2)} Декартовий добуток: Для 2-х відношень r1 (R1) та r2 (R2) операція декартовий добуток визначає відношення, яке вміщує всі комбінації кортежів з r1 та r2. Операцію можна виконувати над будь-якими відношеннями. В результуючому відношенні буде n*m рядків. r1(R1)
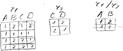
Операція селекція: це унарна операція результатом застосування її до відношення r (R) є відношення r” (R),яке вміщує підмножину кортежів з r з визначниками у виділених атрибутах. Селекція – включає тількі ті рядки, які задовольняють вказаній умові р. Умова р може бути визначення за допомогою >, >=, <=, <, а також логічних і та або. Властивості селекції: оператори селекції комутують відносно їх композиції; Оператор селекції дистрибутивин відносно булевих операцій. На вході використовується одне відношення, результат - нове ставлення, побудоване за тією ж схемою, що містить підмножина кортежів вихідного відносини, що задовольняють умовою вибірки.На вході використовується одне відношення, результат - нове ставлення, побудоване за тією ж схемою, що містить підмножина кортежів вихідного відносини, що задовольняють умовою вибірки. r’(R) = G=a1(r (R))= { tjЄ r1/ ti (A)=a1} Приклад: A B r(AB) GA=a1(r)
Операція проекції - унарна операція, яка визначає певну частину атрибутів по всім кортежам вихідного відношення. Проекція – суть операції полягає в тому, що з початкової схеми вибираються тільки ті стовпчики, які вказані в списку. Операція проекції являє собою вибірку з кожного кортежу відносини значень атрибутів, що входять в список A, і видалення з отриманого відносини повторюваних рядків. Властивості проекції: Якщо 2 проекції виконуються послідовно і друга з них належить першій,то вона поглинається нею; Проекція комутує з селекцією,якщо атрибути для селекції входять у множиину атрибутів проекції/ Пx(r(R)) = { ti(x) / ti є r} Приклад: r(ABCD) ПAC(r)
Операція природного з”єднання-це бінарна операція.в результаті якої отримується відношення з кортежами які комбінують по всім співпадаючим атрибутам. Об’єднання виконується над відношеннями, що мають однакову схему і включає всі кортежі (рядки), які належать хоча б одному з даних відношень. Рядки не дублюються. R1 (R1) |x| r2 (R2) ={ t1 (R1 U R2) / Ti (R1) Є r1, t1 (R2) Є r2}
Якщо одноіменних атрибутів відношення не мають.то виконується операція декартового добутку Еквіз”єднання: виконується комбінування атрибутів по вказаним атрибутам (їх рівності). r1[a1=B1], r2={ tj (R1 U R2)/tj (R1)Є r1; tj (R2)Є r2, tj (A1)Є r1; tj (B1)Є r2} Операція еквіз’єднання називається природним з’єднанням(natural join), якщо в результат проходить лише один стовбчик з двох (в обох стовбчиках у кожному рядочку значення повинні співпадати за визначенням операції еквіз’єднання).
Операція Θ –з”єднання –якщо є 2 відношення r1 та r2 і атрибути А1.А2…Ат Є R1,а В1,В2….Вт Є R2,то операція Θ –з”єднання (тета-з’єднання). r1[A1Θ B1,A2Θ B2,…AnΘ Bn]r2
Операція ділення –є зворотною до операції природного з”єднання r=r1 (R1)/r2(R2)Є r1; tj (R2)Є r2, tj (A1)Є r1; tj (B1)Є r2}
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

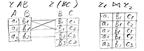 Найпоширеніша трактування реляційної моделі даних належить К. Дейта. Згідно Дейта, реляційна модель складається з трьох частин:
Найпоширеніша трактування реляційної моделі даних належить К. Дейта. Згідно Дейта, реляційна модель складається з трьох частин: r2(R2) = { tj (R1 U R2)/tj (R1)Є r1; tj (R2)Є r2
r2(R2) = { tj (R1 U R2)/tj (R1)Є r1; tj (R2)Є r2