
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра высшей математики и физикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Министерство сельского хозяйства Российской Федерации ФГБОУ ВПО «Вологодская государственная молочнохозяйственная
Кафедра высшей математики и физики
МАТЕМАТИКА
методические указания и контрольные задания для студентов бакалавриата направлений подготовки 35.03.07 Технология производства и переработки сельскохозяйственной продукции, 36.03.02 Зоотехния (заочная и очно-заочная формы обучения)
Вологда–Молочное УДК 51 (071) ББК 22.1 р30 М341 Разработали:
Д.ф.-м.н., заведующийкафедрой высшей математики и физики М.Г. Плотников, к.э.н., доценткафедры высшей математики и физики В.Ю. Ивановская.
Рецензенты:
к.ф.-м.н, доцент кафедры высшей математики и физики Плотникова Ю.А., к.с.-х.н, доцент кафедры земледелия и агрохимии Хамитова С.М.
М341 Математика: Методические указания и контрольные задания для студентов бакалавриата направлений подготовки 35.03.07 Технология производства и переработки сельскохозяйственной продукции, 36.03.02 Зоотехния (заочной и очно-заочной форм обучения) / Составили д.ф.-м.н., заведующийкафедрой высшей математики и физики М.Г. Плотников,к.э.н., доценткафедры высшей математики и физики В.Ю. Ивановская. – Вологда–Молочное: ИЦ ВГМХА, 2014. – 22 с., 3 прил.
Составлено в соответствии с требованиями (федеральный компонент) к обязательному минимуму содержания и уровню подготовки бакалавра и дипломированного специалиста по математическому и естественнонаучному циклу с целью оказания помощи при написании контрольной работы студентами заочной и очно-заочной формы обучения. Предназначено для студентов заочной и очно-заочной формы обучения (бакалавриат направлений подготовки 35.03.07 Технология производства и переработки сельскохозяйственной продукции, 36.03.02 Зоотехния.
Публикуется в соответствии с планом издательской деятельности на 2014 год, утверждённым решением Ученого совета ____2014 года, протокол №__.
УДК 51 (071) ББК 22.1 р30
ãПлотников М.Г., 2014 ãИвановская В.Ю., 2014
ã ИЦ ВГМХА, 2014 Общие методические указания В соответствии с учебным планом студенты-заочники выполняют по курсу высшей математики одну контрольную работу. При выполнении работы студент должен руководствоваться следующими указаниями:
Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и может воспользоваться решением типичных задач, содержащихся в методических указаниях.
Рекомендуемая литература
Тема І. Введение в анализ
[6], задачи 676, 679, 682, 686, 961, 737, 747, 748, 753, 763, 771, 772.
1–10. Задачи контрольной работы. Вычислить указанные пределы. 1. а) 2. а) 3. а)
4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а)
Решение типовых задач
Задача. Найти следующие пределы: а)
Решение. а) Непосредственная подстановка предельного значения аргумента
Заметим, что аргумент б) при
Таблица производных (1) (2) (3) (4) (5) (6) (7)
(8) (9) (10) (11) (12) (13) (14) (15) (16) (17)
11-20. Задачи контрольной работы. Найти производные заданных функций:
11. а) 12. а) 13. а) 14. а) 15. а) 16. а) 17. а)
18. а) 19. а) 20. а) Решение типовых задач Задача. Найти производные заданных функций: а)
Решение. а) Вводя дробные и отрицательные показатели, будем иметь
б) Применяя правило дифференцирования дроби (формула (4) Таблицы производных), получим
При этом по формуле (7) Таблицы производных
а по формуле (13) Таблицы производных
Отсюда:
в) Под знаком производной имеем сложную функцию вида
Далее, применяя формулы (1), (12) Таблицы производных найдем
Тогда
21-30. Задачи контрольной работы. Исследовать данную функцию и построить её график. Исследование предусматривает нахождение точек экстремума и интервалов возрастания и убывания функции, нахождение точек перегиба графика функции и интервалов выпуклости и вогнутости графика.
21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Решение типовой задачи Задача. Исследовать функцию
Решение. Исследуем данную функцию на экстремум с помощью производной. Определим критические точки. Для этого находим первую производную данной функции
Решая последнее уравнение, находим его корни Исследуем критическую точку
Из равенства (*) видно, что при Теперь исследуем критическую точку Вычислим значение функции в точках экстремума:
точки максимума Определим точки перегиба графика функции и интервалы выпуклости и вогнутости. Для этого находим вторую производную
Отсюда
Из правой части равенства (**) следует, что при Как видно, вторая производная
Таким образом,
Рис. 2
Таблица основных неопределенных интегралов
(18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28)
(29) (30)
31-40. Задачи контрольной работы. Найти указанные неопределённые интегралы.
41. а) 42. а) 43. а) 44. а) 45. а) 46. а) 47. а) 48. а) 49. а) 50. а) Решение типовых задач Задача. Найти неопределенные интегралы: а)
Решение. а) Предварительно преобразуем подынтегральную функцию и затем применим свойства неопределённого интеграла и формулу (20) Таблицы интегралов:
= =
б) воспользуемся подстановкой
При вычислении неопределённого интеграла, полученного в результате замены переменной, мы пользовались формулой (21) Таблицы интегралов.
в) В неопределённом интеграле выполним замену
При вычислении неопределённого интеграла
41-50. Задачи контрольной работы. Вычислить с помощью определённого интеграла площадь фигуры, ограниченной параболой и прямой. Сделать чертеж и заштриховать искомую фигуру.
41. 42. 43. 44. 45. 46. 47. 48. 49. 50.
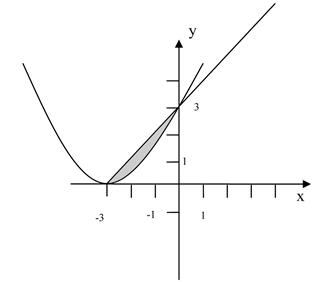
Решение типовой задачи Задача. Вычислить площадь фигуры, ограниченной параболой
Решение. Площадь фигуры, ограниченной сверху непрерывной кривой
Найдем точки пересечения заданных параболы и прямой. Составим и решим систему их уравнений:
Подставив в первое уравнение системы вместо у сумму х + 3, получим:
Отсюда, Из формулы (***) следует, что площадь фигуры равна
= =
Следовательно, искомая площадь равна 1,5 кв. ед. Рассмотренная фигура изображена на рисунке.
Рис. 3 Решение типовой задачи
Задача. Найти значение биомассы в момент Т=12, если в начальной момент (при t=0) значение биомассы
Решение. Составим дифференциальное уравнение, описывающее динамику развития популяции. Скорость изменения биомассы характеризуется производной Это уравнение является дифференциальным уравнением с разделяющимися переменными. Разделим переменные m и t:
Отсюда после почленного интегрирования получаем:
(в данном случае произвольную постоянную удобно взять в виде
Для определения значения произвольной постоянной С полагаем
Таким образом, из общего решения дифференциального уравнения приходим к выражению
Положим теперь в этом равенстве
Следовательно, в момент Задачи контрольной работы
61. В зоологическом саду имеются 10 розовых пеликанов. Из них 4 самки. Найти вероятность того, что наудачу будет выбран самец? 62. В окно влетело 5 мух, а в двери 3 мухи. Какова вероятность того, что первая попавшаяся муха оказалась влетевшей через окно? 63. В корзине 12 плодов. Из них 4 груши. Найти вероятность того, что первый взятый плод окажется грушей? 64. В стаде пасется 40 овец, причем 30 из них — романовской породы. Найти вероятность того, что наудачу выбранная овца окажется не романовской породы? 65. В магазине было куплено 100 яиц. Четыре из них оказались треснутыми. Какова вероятность того, что наудачу взятое яйцо окажется целым?
66. В ящике 10 гусиных и 15 утиных яиц. Найти вероятность того, что первое взятое яйцо окажется утиным? 67. В табуне 20 лошадей, из них 12 вороных и 8 белых. Найти вероятность того, что наудачу взятая лошадь окажется белой масти? 68. У кошки родились 5 котят, причем 3 белых, а 2 черных. Найти вероятность того, что наудачу взятый котенок окажется черным? 69. В стае 30 голубей, из них 5 породы турман. Какова вероятность того, что первый наудачу взятый голубь не окажется породы турман? 70. В табуне пасется 55 лошадей. Из них 15 лошадей арабской породы. Наудачу выбирают одну лошадь. Найти вероятность того, что она окажется арабской породы? Решение типовой задачи Задача. В стаде из 70 телят заболели 3 теленка. Какова вероятность того, что наудачу взятый теленок окажется здоровым? Решение. Пусть событие А состоит в том, что случайно выбранный теленок здоров. Случайный отбор подразумевает, что все исходы события А равновозможные. Всего исходов 71-80. Задачи контрольной работы. Задан закон распределения случайной величины в виде таблицы; в первой строке таблицы указаны возможные значения случайной величины Х, во второй – соответствующие вероятности. Вычислить: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
Решение типовой задачи Задача. Задан закон распределения дискретной случайной величины Х.
Вычислить: 1) математическое ожидание; 2) дисперсию; Решение. 1) математическое ожидание дискретной случайной величины вычисляется по формуле:
Подставляем данные задачи в формулу, получаем
=
2) дисперсия дискретной случайной величины вычисляется по формуле:
Подставляем сюда данные
+ 35,378+3,669+0,196+11,858+21,609=73,01.
3) среднее квадратическое отклонение находится по формуле:
Содержание
Общие методические указания...................................................................... 3 Рекомендуемая литература........................................................................... 4 Тема І. Введение в анализ.............................................................................. 4 Тема II. Дифференциальное исчисление........................................................ 6 Тема ІII. Элементы интегрального исчисления........................................... 12 Тема IV. Дифференциальные уравнения.................................................... 17 Тема V. Основы теории вероятностей......................................................... 18 Тема VI. Основы математической статистики.…...…………………………..22 Содержание ….......................................................................................................22
Министерство сельского хозяйства Российской Федерации ФГБОУ ВПО «Вологодская государственная молочнохозяйственная
Кафедра высшей математики и физики
МАТЕМАТИКА
методические указания и контрольные задания для студентов бакалавриата направлений подготовки 35.03.07 Технология производства и переработки сельскохозяйственной продукции, 36.03.02 Зоотехния (заочная и очно-заочная формы обучения)
Вологда–Молочное УДК 51 (071) ББК 22.1 р30 М341 Разработали:
Д.ф.-м.н., заведующийкафедрой высшей математики и физики М.Г. Плотников, к.э.н., доценткафедры высшей математики и физики В.Ю. Ивановская.
Рецензенты:
к.ф.-м.н, доцент кафедры высшей математики и физики Плотникова Ю.А., к.с.-х.н, доцент кафедры земледелия и агрохимии Хамитова С.М.
М341 Математика: Методические указания и контрольные задания для студентов бакалавриата направлений подготовки 35.03.07 Технология производства и переработки сельскохозяйственной продукции, 36.03.02 Зоотехния (заочной и очно-заочной форм обучения) / Составили д.ф.-м.н., заведующийкафедрой высшей математики и физики М.Г. Плотников,к.э.н., доценткафедры высшей математики и физики В.Ю. Ивановская. – Вологда–Молочное: ИЦ ВГМХА, 2014. – 22 с., 3 прил.
Составлено в соответствии с требованиями (федеральный компонент) к обязательному минимуму содержания и уровню подготовки бакалавра и дипломированного специалиста по математическому и естественнонаучному циклу с целью оказания помощи при написании контрольной работы студентами заочной и очно-заочной формы обучения. П
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.85.47 (0.015 с.) |

 , гл. VІ, §§ 1–9; гл. VІІ, §§; гл. VІІІ, §§ 1–6;
, гл. VІ, §§ 1–9; гл. VІІ, §§; гл. VІІІ, §§ 1–6; , гл. І, §§ 1–9; гл. ІІ;
, гл. І, §§ 1–9; гл. ІІ; б)
б) 
 б)
б) 
 б)
б) 
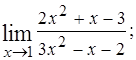 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
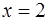 приводит к неопределённому выражению вида
приводит к неопределённому выражению вида  . При
. При  числитель и знаменатель дроби — бесконечно малые величины. Чтобы раскрыть такого вида неопределенность, необходимо предварительно дробь преобразовать. Разложим на множители числитель и знаменатель дроби и сократим их на
числитель и знаменатель дроби — бесконечно малые величины. Чтобы раскрыть такого вида неопределенность, необходимо предварительно дробь преобразовать. Разложим на множители числитель и знаменатель дроби и сократим их на  :
: .
. только стремится к своему предельному значению 2, но не совпадает с ним. Следовательно, разность, т.е. множитель, на который мы сокращаем, отличен от нуля при
только стремится к своему предельному значению 2, но не совпадает с ним. Следовательно, разность, т.е. множитель, на который мы сокращаем, отличен от нуля при  .
. получаем неопределённое выражение
получаем неопределённое выражение  . Чтобы найти предел дробно-рациональной функции
. Чтобы найти предел дробно-рациональной функции  при
при  , где
, где 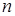 – наивысшая из степеней многочленов
– наивысшая из степеней многочленов  и
и  . Разделим числитель и знаменатель данной дроби на
. Разделим числитель и знаменатель данной дроби на  и применим основные теоремы о пределах, свойства бесконечно малых величин:
и применим основные теоремы о пределах, свойства бесконечно малых величин: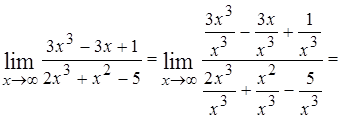

 , где с – произвольная постоянная.
, где с – произвольная постоянная.
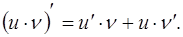


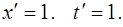
 a – любое действительное число,
a – любое действительное число,











 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 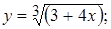
 б)
б) 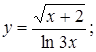 в)
в) 
 б)
б) 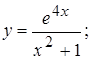 в)
в)  .
. б)
б)  в)
в) 
 Применяя правило дифференцирования суммы (формула (2) Таблицы производных), формулу дифференцирования степенной функции (7) Таблицы производных и формулу дифференцирования постоянной (5) Таблицы производных, получаем:
Применяя правило дифференцирования суммы (формула (2) Таблицы производных), формулу дифференцирования степенной функции (7) Таблицы производных и формулу дифференцирования постоянной (5) Таблицы производных, получаем:
 .
. ,
, .
.
 , где
, где  — промежуточный аргумент. Используя формулу (7), получим:
— промежуточный аргумент. Используя формулу (7), получим: .
.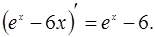
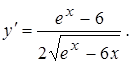



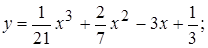





 .
. на экстремум и определить интервалы её возрастания и убывания. Найти точки перегиба графика этой функции и определить интервалы его выпуклости и вогнутости. Построить график данной функции.
на экстремум и определить интервалы её возрастания и убывания. Найти точки перегиба графика этой функции и определить интервалы его выпуклости и вогнутости. Построить график данной функции. и приравниваем её к нулю:
и приравниваем её к нулю:
 и
и  Таким образом,
Таким образом,  — критические значения аргумента. Так как производная
— критические значения аргумента. Так как производная  . Определим знак первой производной левее и правее этой точки в достаточно малой её окрестности. Производную
. Определим знак первой производной левее и правее этой точки в достаточно малой её окрестности. Производную  . (*)
. (*)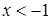 производная
производная  производная
производная 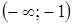 функция возрастает, а в интервале
функция возрастает, а в интервале 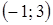 - убывает. Так как производная
- убывает. Так как производная 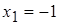 меняет свой знак с плюса на минус, то в этой точке функция имеет максимум.
меняет свой знак с плюса на минус, то в этой точке функция имеет максимум.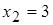 . Из равенства (*) видно, что при
. Из равенства (*) видно, что при  производная
производная 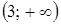 функция возрастает. Так как производная
функция возрастает. Так как производная 
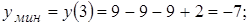
 и минимума
и минимума  отмечены на рисунке, где показан график исследуемой функции.
отмечены на рисунке, где показан график исследуемой функции.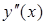 , приравниваем её к нулю и находим действительные корни уравнения
, приравниваем её к нулю и находим действительные корни уравнения  :
:
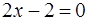 .
. критическая точка второго рода. Запишем вторую производную в виде:
критическая точка второго рода. Запишем вторую производную в виде: . (**)
. (**) вторая производная
вторая производная 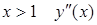 положительна. Следовательно, в интервале
положительна. Следовательно, в интервале 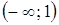 график функции является выпуклым, а в интервале
график функции является выпуклым, а в интервале  — вогнутым.
— вогнутым. меняет свой знак. Следовательно,
меняет свой знак. Следовательно,  .
.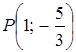 – точка перегиба графика функции.
– точка перегиба графика функции.

 и т.д.
и т.д.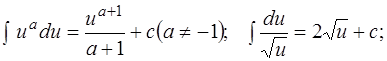










 , где А — любое действительное число.
, где А — любое действительное число. б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б) 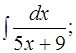 в)
в) 
 б)
б)  в)
в) 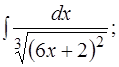
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б) 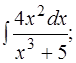 в)
в) 
 =
= 


 , тогда
, тогда  , откуда
, откуда  . Таким образом,
. Таким образом,
 =
=  .
. , чтобы привести его к табличному виду. Тогда
, чтобы привести его к табличному виду. Тогда  . Получим:
. Получим:
 была использована формула (20) Таблицы интегралов.
была использована формула (20) Таблицы интегралов.

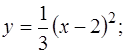









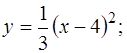
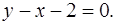


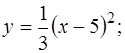



 и прямой
и прямой  , снизу — непрерывной кривой
, снизу — непрерывной кривой  , слева — прямой
, слева — прямой  , справа — прямой
, справа — прямой  , вычисляется по формуле:
, вычисляется по формуле: . (***)
. (***) .
. ,
,  ,
,  ,
, ,
,  .
.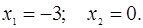 Тогда
Тогда  Таким образом, парабола и прямая пересекаются в точках
Таким образом, парабола и прямая пересекаются в точках  и
и 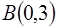 .
.
 =
= 

 и
и 
 (при
(при  — это скорость развития, при
— это скорость развития, при  — скорость вымирания). По условию задачи
— скорость вымирания). По условию задачи  или
или 

 , т.е.
, т.е.  .
. . Из последнего равенства следует формула для общего решения дифференциального уравнения:
. Из последнего равенства следует формула для общего решения дифференциального уравнения: .
. В результате получаем:
В результате получаем:

 Тогда
Тогда
 (ед.) значение биомассы будет составлять 50 (ед.).
(ед.) значение биомассы будет составлять 50 (ед.). , исходов, благоприятствующих событию А,
, исходов, благоприятствующих событию А,  . Следовательно, искомая вероятность Р (А) =
. Следовательно, искомая вероятность Р (А) = 





 .
. .
. , получаем:
, получаем:





