
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики сау (сар) в отклоненияхСодержание книги
Поиск на нашем сайте
При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики. На рис. 2.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) - входное воздействие, а y(t) - выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие - регулируемой величиной (переменной).
Рис. 2.1 – Схематическое представление САУ (звена) При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др. Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др.. В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др. Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).
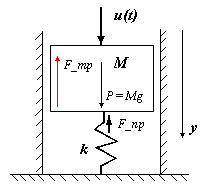
В качестве примера рассмотрим «технологию» получение уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.2.
Рис. 2.2 – Механический демпфер Согласно 2-го закона Ньютона Þ...ускорение тела равно сумме сил… Þ
где m – масса тела; Fj - силы, воздействующие на тело (поршень демпфера).
Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем Þ
где m∙g – сила тяжести; k∙y(t) – сила сопротивления пружины; Размерности сил и коэффициентов, входящих в уравнение (2.1.2) Þ
Предполагая, что при t £ 0 поршень демпфера находился в равновесии Þ
Пусть при t > 0 Þ Подставляя эти соотношения в уравнение (2.1.2), получаем
Если t £ 0, уравнение (2.1.3) принимает вид:
Соотношение (2.1.4) - уравнение звена (демпфера) в стационаре, а соотношение (2.1.5) - статическая характеристика звена (демпфера). Þ см. рисунок ниже Þ
Рис. 2.3 – Статическая характеристика механического демпфера Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:
где Уравнение (2.1.6) - это уравнение динамики в канонической форме, т.е. коэффициент при Dy(t) равен 1.0!!! «Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл постоянных времени. Þ В самом деле Þ
Таким образом, получаем, что: - коэффициент перед первой производной имеет размерность Þ [c] Þ т.е. смысл некоторой постоянной времени; - коэффициент перед второй производной Þ [c2]; - коэффициент в правой части Þ [м-1] Тогда уравнение (2.1.6) можно записать в операторной форме:
где p = d / dt – оператор дифференцирования;
N(p) - линейный дифференциальный оператор, вырожденный в Const, равную k 1 . Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на ЭВМ (поскольку числа в ЭВМ представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной Þ Введем новые нормированные (безразмерные) переменные:
Подставляя эти соотношения в уравнение (2.1.2), имеем:
Перенося в левую часть члены, содержащие
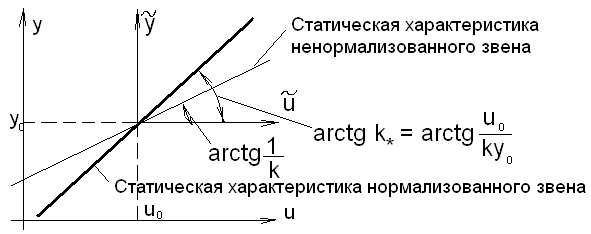
где Проверим размерность коэффициента Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления. На рис. 2. 4 представлены статические характеристики для механического демпфера.
Рис. 2.4 Процедура нормировки отклонений позволяет привести уравнения динамики к виду:
где L(p), N(p) – дифференциальные операторы. Если дифференциальные операторы L(p) и N(p) - линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ). А если L(p) или N(p) – нелинейные дифференциальные операторы, или
|
||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |



 (2.1.1)
(2.1.1) (2.1.2)
(2.1.2)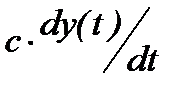 – сила трения.
– сила трения.
 Þ перейдем к отклонениям от стационарного состояния Þ
Þ перейдем к отклонениям от стационарного состояния Þ
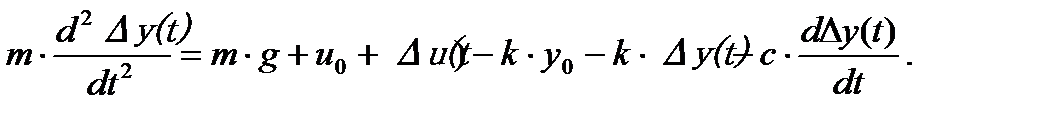 (2.1.3)
(2.1.3)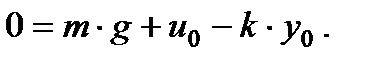 Þ (2.1.4)
Þ (2.1.4)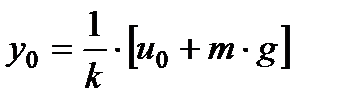 . (2.1.5)
. (2.1.5)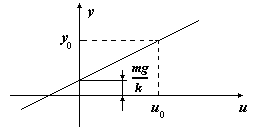
 Þ разделив на k, имеем Þ
Þ разделив на k, имеем Þ (2.1.6)
(2.1.6)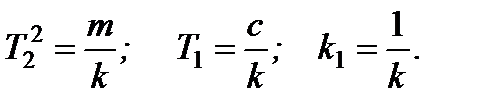
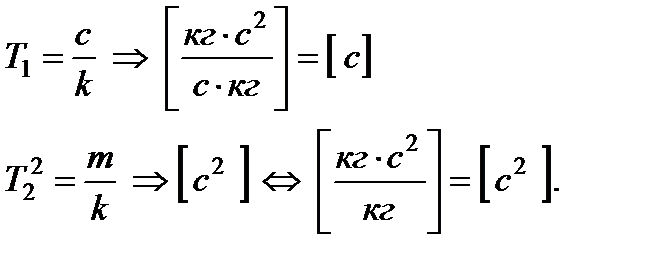
 (2.1.6.а)
(2.1.6.а) - линейный дифференциальный оператор;
- линейный дифференциальный оператор;
 Þ
Þ
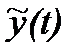 , и разделив на
, и разделив на 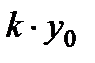 , получаем:
, получаем: (2.1.7)
(2.1.7)
 - коэффициент усиления, причем безразмерный ===>
- коэффициент усиления, причем безразмерный ===>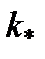 ==>
==>  .
.
 (2.1.8)
(2.1.8)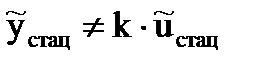 , то уравнение динамики - нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).
, то уравнение динамики - нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).


