
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Единичное гармоническое воздействие
Данное воздействие используется для анализа частотных характеристик САУ (звена) в установившемся режиме колебаний в системе, т.е. свойства САУ (звена) исследуются при больших значениях t (времени), когда влияние начальных условий пренебрежимо мало и движение (колебания) системы определяются только входным внешним воздействием.
x(t) = sin wt, (2.4.4)
где w - круговая частота, [1/с]; w = 2pf, где f - частота в Герцах. На рисунке 2.13 представлен график единичного гармонического воздействия.
Рисунок 2.13 Поскольку при анализе частотных характеристик САУ рассматривается режим установившихся вынужденных колебаний САУ (при больших значениях времени t Þ когда собственная составляющая переходного процесса пренебрежимо мала), то удобнее представить x(t) в показательной форме. Þ
Необходимо отметить, что показательная форма – «комплексное » воздействие. Þ
Действительная часть «комплексного » воздействия (Re) – на самом деле косинусоидальное воздействие. Но так как частотные характеристики САУ определяются в режиме установившихся гармонических колебаний (т.е. при «очень-очень» больших значениях t), то не важно, по какому закону вводилось единичное гармоническое воздействие – по «синусу» или по «косинусу».
Линейное воздействие
Данный вид входного воздействия используется для оценки точности систем управления, а именно, для определения скоростных ошибок. x(t) = a∙t, (2.4.7) где t ³ 0, а при t < 0 входное воздействие всегда равно нулю. На рисунке 2.14 представлен график линейного входного воздействия.
Рисунок 2.14 – Линейное входное воздействие
2.5. Основные положения и свойства интегральных преобразований Лапласа
Решение однородного обыкновенного дифференциального уравнения (ОДУ) усоб(t) записывается в виде (если нет повторяющихся корней):
т.е. все члены уравнения имеют одну и ту же форму. Этот результат наводит на мысль, а нельзя ли ввести какое-то преобразование, в результате которого уравнение динамики (дифференциальное) можно привести к чисто алгебраическому, решение которого не представляет проблем. А если затем сделать соответствующее обратное преобразование, то получим у соб (t). Þ
Þ Обыкновенное дифференциальное уравнение (ОДУ) ® Алгебраическое уравнение Þ Решение Þ ® Обратное преобразование Þ Результат. Именно такими соображениями руководствовался Лаплас, предлагая такое преобразование, называемое в настоящее время преобразованием Лапласа. Þ Предположим, что имеется нестационарный процесс f(t). Þ Лаплас предложил ввести интегральное преобразование, которое отображает f(t) на комплексную плоскость по соотношению: Þ
iIm
Re
Рисунок 2.15 где s = c+i×w: w Î ] -¥; +¥ [; с – абсцисса абсолютной сходимости (обычно в курсе «УТС» с = 0); f(t) – прообраз (оригинал); F(s) – изображение (образ); Символическое обозначение преобразования Лапласа:
f(t)
Преобразования Лапласа существует, если:
а также при t< 0 f(t)= 0. f (t) iIm F(s) s = s 1 = c+ i×w Þ Re f (t) s = s 2 = c + i×w 2 t s = s 3 = c + i×w 3 s = s 6 s = s 4 s = s 5 Рисунок 2.16 Рисунок 2.17 В соответствии с соотношением (2.5.1) переходной процесс f(t) отображается на комплексную плоскость, где каждому значению оператора Лапласа «s» соответствует свой вектор. Þ Линия, соединяющая концы векторов называется годографом. Обратное преобразование Лапласа определяется следующим соотношением:
Необходимо подчеркнуть, что если условие сходимости выполняется, то любомуоригиналу соответствует изображение. Обратное преобразование Лапласа не всегда существует, т.е. если известно F(s), это не означает, что ему соответствует оригинал f(t)!!! Прямое преобразование Лапласа символически обозначается:
f(t)
Обратное преобразование Лапласа обозначается: F(s)
Существует двухстороннее преобразование Лапласа LB [f(t)], частным случаем которого является обычное преобразование Лапласа Þ
Если при t £ 0 функция f(t) = 0, то L B [ f(t) ] º L [ f(t) ]. Частным случаем двухстороннего преобразования Лапласа (при с = 0, т.е. s = i×w) является преобразование Фурье, определяемое соотношениями:
2.5.1. Использование преобразования Лапласа для операции дифференцирования
Пусть известно f(t) и его изображение по Лапласу: (f(t)
Воспользуемся соотношением (2.5.1) Þ
где f(0) – начальное условие. Если начальные условия равны нулю Þ f(0) = 0;
Аналогичным способом найдем изображение 2-ой производной Þ
Если при t = 0 f(t) и f `(0) равны нулю (нулевые начальные условия), то Þ
Обобщая на производную n -го порядка при нулевых начальных условиях, имеем:
2.5.2. Использование преобразования Лапласа для операции интегрирования
Пусть известно преобразование f(t) Окончательно:
Если начальные условия равные нулю:
2.6. Основные свойства преобразований Лапласа Свойство линейности
Пусть есть процессы f1(t) и f2(t), каждый из которых имеет свое изображение по Лапласу: f1(t)
Если f(t)=a× f1(t), то:
2.6.2. Свойство подобия (свойство изменения масштаба)
Пусть f(t)
|
||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.200.66 (0.013 с.) |

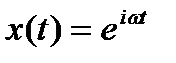 (2.4.5)
(2.4.5) (2.4.6)
(2.4.6)

 c (2.5.1)
c (2.5.1) F(s) (2.5.2)
F(s) (2.5.2) , - условие сходимости, (2.5.3)
, - условие сходимости, (2.5.3)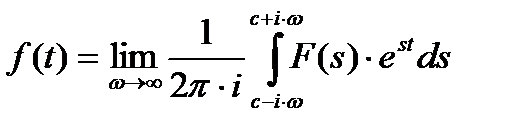 (2.5.4)
(2.5.4) (2.5.5)
(2.5.5) (2.5.6)
(2.5.6) (2.5.7)
(2.5.7) (2.5.8)
(2.5.8) Þ
Þ
 (2.5.9)
(2.5.9) (2.5.9.а)
(2.5.9.а)
 (2.5.10)
(2.5.10) (2.5.10.а)
(2.5.10.а)
 (2.5.11)
(2.5.11) ??? Þ по аналогии с предыдущим Þ
??? Þ по аналогии с предыдущим Þ
 (2.5.12)
(2.5.12) (2.5.13)
(2.5.13) Þ то Þ
Þ то Þ (2.6.1)
(2.6.1) (2.6.2)
(2.6.2) ??? Þ
??? Þ Þ
Þ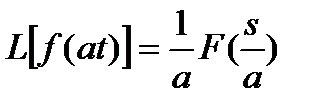 (2.6.3)
(2.6.3)


