Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Апериодическое звено 1 – го порядка (инерционное звено)
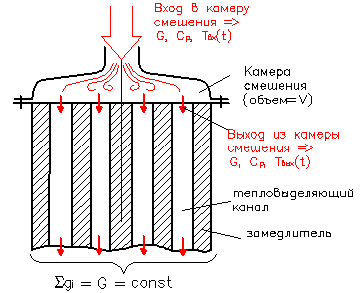
Вывод свойств (характеристик) апериодического звена сделаем на примере фрагмента (части) ядерного, а именно – входной камеры смешения.
Сделаем следующие допущения: 1) расход теплоносителя постоянен => G = const; 2) теплоемкость теплоносителя = const = Cp; 3) входящий в камеру смешения теплоноситель полностью перемешивается в камере смешения, т.е. температура жидкости, поступающий в каждый тепловыделяющий канал одинакова; 4) теплообмен камеры смешения с окружающей средой пренебрежимо мал. Уравнение теплового баланса
где ρ – плотность теплоносителя, Ср – удельная теплоемкость, V – объем камеры смешения G – расход теплоносителя, Твх(t), Твых(t) – температура теплоносителя на входе и выходе, соответственно. Т(t) – температура (перемешанного) теплоносителя в камере смешения => T(t) ≡ Tвых(t) Условие стационара соответствуют приравниванию нулю левой части уравнения
Введем новые переменные:
Подставляя эти соотношения в (3.3.1), получаем:
Сокращая на Т0 и Ср
τ – постоянная времени
1 – аналог К;
Таким образом получили линейное дифференциальное уравнение, причем решенные Уравнение (3.3.3) соответствует типовому апериодическому звену первого порядка:
В общем случае уравнение динамики апериодического звена 1-го порядка имеет вид:
Если начальные условия нулевые, то y(t) y’(t) x(t) Уравнение динамики в изображениях => [T·s+1] ·Y(s) = K·X(s) (3.3.5) Передаточная функция апериодического звена 1 - го порядка: Найдем выражение для АФЧХ => s = i∙ω => W(iω) = W(s)│s=iω= умножим на комплексно – сопряженное значение (1 – i∙T∙ω) =>
Подставляя в формулы (3.3.8) различные значения частоты ω найдем соответствующее значение u (ω) и v (ω) => построим эти вектора на комплексной плоскости:
Анализ показывает, что годограф АФЧХ — полукруг радиусом = K => φ3 = φ(ω3) = - Из формулы (3.3.7)
Учитывая, что годограф АФЧХ находится в IV-ой квадранте, то =>
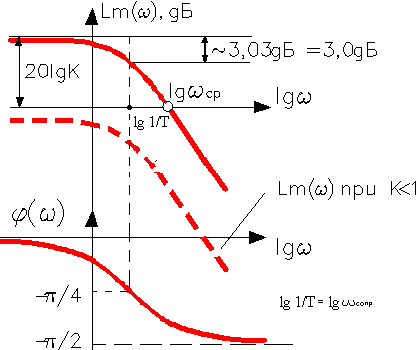
ЛАХ => Lm (ω) = 20 lg A (ω) = 20 lg K – 20 lg Lm (ω) =20 lg K – 20 lg
Анализируя частотные свойства данного звена => 1) При ω << свойства звена приблизительно совпадают со свойствами идеального усилительного звена, т.е. W(iω) ≈ K => W(s) ≈ K. 2) При ω >> свойства звена приблизительно совпадают со свойствами идеального интегрирующего звена, т.е. W(iω) ≈ => W(s) ≈. 3) При ω ≈ => на свойства звена оказывают примерно равное “влияние” свойства идеального усилительного и идеального интегрирующего звена. Принято называть частоту, при которой происходит “излом” ЛАХ (ωсопр =) => − сопрягающей частотой или => ωсопр = => причем не трудно показать, что при ωсопр = величина амплитуды А(ωсопр) меньше А(0) = К в Частотой среза ωср называют такое значение частоты, при которой модуль (амплитуда) выходного сигнала (воздействия) = 1,0 => А(ωср) = => ωср= => если K>>1 ωср= Если K < 1, то частота среза не существует!!!
Найдем переходную функцию звена (реакция на единичное ступенчатое воздействие)
Рис. Переходная функция Рис. Весовая функция Постоянная времени Т характеризует инерционность переходных процессов в звене => чем больше Т, тем инерционнее звено (т.е. медленнее идет переходной процесс). Примерами апериодического звена 1- го порядка являются: 1) Пассивные R−L или R−C цепочки =>
2) упрощенная модель гидротурбины, где x(t) = приводной момент; y(t) − скорость вращения ротора турбины. 3) электродвигатель (постоянного тока или асинхронный) с учетом инерционности якоря (ротора), где x(t) − например, напряжение в обмотке возбуждения, а y(t) − скорость вращения якоря (ротора) => выходного вала; 4) тепловые датчики, например, термопара, где: x(t) − температура одного (“горячего”) спая, а y(t) − термо Э.Д.С. 5) выходная камера смешения в реакторе (приближенно) 6) различные элементы реактора, описываемые в рамках точеных моделей (например, активная зона или ядерное горючее) с использованием закона Фурье:
где T(t) − температура топлива;
Т* − например, температура кипения теплоносителя. 3.4. Апериодическое звено 2−го порядка Уравнение динамики апериодического звена 2−го порядка имеет следующий вид:
Если D < 0, то звено становится колебательным (см. 3.5) Учитывая, что: y(t) Передаточная функция звена может быть представлена в двух видах:
где T3= −
Амплитудно − фазовая частотная характеристика (АФЧХ) =>
Домножив формулу (3.4.5) на комплексно − сопряженные скобки (
Модуль АФЧХ (амплитуда) = mod W(i·ω) = | W(i·ω)| =>
Подставляя в формулы (3.4.6) или в формулу (3.4.5) различные значения ω можно построить вектора, соответствующие различным значениям ω:
Очевидно, что 1) ω6 > ω5 > ω4 > ω3 > ω2 > ω1 > 0 2) 0 > φ1 > φ2 > φ3 > φ4 > φ5 > φ6 Нетрудно показать, что Из данного рисунка видно, что φ(ω) є [0; –π[, а точнее φ(ω) є [ -π; 0]. Используя формулу для фазового сдвига: Более удобная формула получается, если использовать “последовательное соединение” 2-х звеньев => известно, что при последовательном соединении звеньев общий сдвиг фазы равен сумме фазовых сдвигов:
Логарифмическая амплитудная характеристика (ЛАХ) = Lm(ω) => Lm(ω) = 20 lg A(ω) => Графики А(ω), φ (ω), Lm(ω) имеют вид:
В инженерных расчетах часто график Lm(ω) представляют виде отрезков ломаных, тогда при при при В граничном случае (D=0 или T1=2·T2) => T3 = T4 и отмеченные на графике Lm(ω) => см. рис. выше => точки «излома» совпадают =>
Если D < 0 (T1 = 2·T2) => звено “переходит” в разряд колебательных звеньев. Поэтому постоянная Т1 в уравнении динамики (3.4.1) играет роль демпфирующего фактора => увеличение Т1 (в колебательном звене) приводит к уменьшению или к полному исчезновению колебаний. Найдем переходную функцию звена h (t) − реакцию на воздействие 1 (t):
Дифференцируя формулу (3.4.10), т.к. w (t) = h ’(t) =>
Примерами апериодического звена 2-го порядка являются: 1) двигатель постоянного тока при учете инерционности самого якоря (механической) и цепи якоря (электрической); 2) электрический усилитель с учетом инерционности (механической и электрической) ротора; 3) двойные R − C или R − L цепочки
Если звено представлено в переменных состояния => x’=Ax + Bu; A= звено будет апериодическим 2-го порядка, если:
Колебательное звено является наиболее “интересным” из всех типовых звеньев, во-первых, за счет “сильной похожести” по своим динамическим свойствам на более сложные реальные САУ (САР), во-вторых, близкой идентичности переходных процессов в звене к аналогичным в реальных САР, и, в-третьих, существенной зависимости динамических свойств от величины параметра звена.
Уравнение динамики звена описывается уравнением, аналогичным рассмотренном в предыдущем разделе (апериодическое звено второго порядка):
причем T1 < 2T2, т.е. D = T12 − 4T22 ≤ 0 Учитывая, что D ≤ 0, удобнее представить уравнение динамики в другой форме, а именно: Введем новые параметры: T ≡ T2 и β = T1 / 2T2 , где β − параметр (коэффициент) затухания (демпфирования (0 ≤ β ≤ 1)). Будем в дальнейшем называть “β” − коэффициентом демпфирования или параметром затухания. Подставляя новые параметры в (3.5.1)
Наиболее удобная форма представления уравнения динамики. Учитывая, что x(t)
Отсюда выражение для передаточной функции:
передаточная функция колебательного звена. Еще раз подчеркнем, что параметр (коэффициент) затухания (демпфирования) 0 ≤ β ≤ 1, причем при β = 1 − свойства колебательного звена совпадают с аналогичными свойствами соответствующего апериодического звена 2-го порядка, а при β = 0 − звено выражается в консервативное, в котором могут существовать незатухающие гармонические колебания. Выражение для АФЧХ получается после подстановки в (3.5.3) значения s = i·ω =>
Выражения для вещественной и мнимой частей принимают вид:
Опуская выкладки запишем выражение для A(ω) и φ(ω)
Анализ формул (3.5.7 − 3.5.9) показывает, что:
Одной из главных особенностей АФЧХ является возможность существования экстремума в зависимости A(ω) => Выполним исследование на экстремум =>
Очевидно, что ωм существует (т.е. є Rе), если (1-2β2) ≥ 0 => Если β < Анализ вышеприведенных соотношений показывает, что при β < Частоту ωм будем отождествлять с тем значением частоты входного гармонического воздействия при которой имеет место максимальное значение амплитуды выходного сигнала. Подставляя выражение для ωм (формула (3.5.10)) в выражение (3.5.8), получаем:
Данная формула работает только при Очевидно, что если β ↓, A(ωм) ↑, а при β → 0, A → ∞. Поскольку β = T1 / 2T2 , то очевидна ‘роль’ постоянных времени: => T2 – ‘раскачивает’ колебания, а T1 − ‘демпфирует’ их. => рассмотрим соответствующие графики:
РИСУНОК
Данные графики аналогичны для случаев резонансов в теоретической механика, физике, электротехнике и т.д. Величину ω = 1 / T принято называть частотой свободных колебаний и обозначать: ω0 = 1/T В звене при β = 0 устанавливаются незатухающие колебания с частотой ω0, а само звено вырождается в консервативное. Подставляя различные значения ω в формулу (3.5.6) или (3.5.7) построим гадограф АФЧХ на комплексной плоскости:
‘легко показать’, что ω4 = 1 / T годограф консервативного звена.
Построение ЛАХ ≡ Lm(ω) не может быть сделано так просто, как для предыдущих позиционных звеньев, т.е. отрезками прямых. Будем использовать для построения графика ЛАХ нормированную (безразмерную) частоту
Введя новую переменную
Такая форма представления позволяет ‘свести’ различные ЛАХ при различных Т к автомодельному виду (‘универсальному’ виду графиков). На рис. … представлен график Lm(ω) в форме (3.5.12) построенный фактически в логарифмических координатах, причем коэффициент усиления K=1. Подчеркнем, что при такой форме представления все ЛАХ при различных T1 и T2 можно “собирать вместе”. Величина Hm (см. рис.) называется превышением:
− превышение при частоте ω = ωm Если
при ω = ωm (эта формула для “ярко выраженных” “горбов”). Вычислим переходную функцию звена h(t) =>
Найдем полюса
Для вычисления составляющей при j = 1 удобнее использовать второй вариант формулы (3.5.15) => j = 1 =>
j = 2 =>
j = 3 => Замечая много общих сомножителей в слагаемых для j = 2, 3 => суммируем составляющие при j = 2 и j = 3 =>
подставляя значения m и n =>
Величина Таким образом в описании колебательного звена появилось три “новых” частоты =>
ωm < ωc < ω0
Рассмотрим предельные случаи для β (т.е. β = 1 и β = 0) Если Если Если
− переходная функция консервативного звена =>
Если
эта формула соответствует также аналогичной формуле для апериодического звена 2- го порядка при D = 0
(совпадающие полюса).
Если
Дифференцируя во времени формулы (3.5.16 − 3.5.18) найдем соответствующие весовые (w (t)) функции: Если
Если
Если
Примерами колебательного звена можно считать:
СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ 4.1. Замена цепи из последовательно параллельно соединенных звеньев
Все реальные системы автоматического регулирования являются замкнутыми и сложными, но при анализе часто приходится рассматривать “фрагменты” (а иногда и целиком) САР и выполнять над ними некоторые операции, например, упрощающие изображение структуры САР. Определение. Действия, упрощающие математическое или графическое изображение САР или упрощающие последующий анализ динамических свойств САР, называются структурными преобразованиями. Различают несколько типовых упрощающих действий: § замена цепи из последовательно соединенных звеньев эквивалентным звеном; § замена цепи из параллельно соединенных звеньев эквивалентным звеном; § замена цепи с местной обратной связью эквивалентным звеном; § замена цепи с местной обратной связью на единичною обратную связь; § перенос точек включения обратной связи “вперед”- “назад”; § перенос точек суммирования или ветвления “вперед”- “назад”.
Рассмотрим поочередно вышеперечисленные структурные преобразования.
4.1.1. Замена цепи последовательно соединенных звеньев эквивалентным звеном
Цепь преобразований: Получить эквивалентную передаточную функцию Wэкв(S) => Wэкв (s) = Y(s)/X(s) ≡ Xn(s)/X(s) => запишем ряд очевидных равенств:
перемножим, соответственно, правые и левые части этих равенств => W1*W2 *……* Wn= X1/X * X2/X1…… Xn-1/Xn-2 * Xn/Xn-1 => Xn (s) /X (s) = Wэкв (s) = W1 (s) *W2 (s) *……* Wn (s)
Найдем эквивалентную АФЧХ => s = i*ω =>
учитывая, что Wj = Aj (ω) eiφj (ω) =>
Эквивалентная логарифмическая амплитудная характеристика =>
Если каждое из звеньев имеет передаточную функцию в виде Wj (s)= K*N (s) /L (s), где N (s), L (s) имеют свободные члены = 1,0 =>
4.1.2. Замена цепи из параллельно соединенных звеньев эквивалентным звеном
Складывая, получаем X1 (s) +X2 (s) +…+ Xn (s) = X (s)[ W1 (s) +W2 (s) +…+ Wn (s)] └─────────────┘ └──────────────┘ ↓ ↓ Y(s) Wэкв(s)
=>
Подставляя вместо “s” значение “i*ω” =>
A экв(ω) не выражается простым сложением =>
Аналогично для фазового сдвига =>
φэкв (ω) =-π*m+arct (Vэкв (ω) / Uэкв (ω)), (4. 10) где значение m: m=1,3,5…, если в 2…3 квадрантах m=0,2,4…, если в 1 или 4 квадрантах Логарифмическая амплитудная характеристика:
Наиболее простые соотношения имеют место для переходной и весовой эквивалентных функций hэкв (t)=
Последовательное и параллельное соединение звеньев в значительной степени похожи на аналогичные соединения в электротехнике, гидравлики, и т.д.
Пример на использование структурных преобразований Задание: Построить (качественно) ЛАХ следующей цепи из последовательно соединенных звеньев: x(t) y(t) → τ1s/(T1*s+1) → K2/(T2*s+1) → K3/(T3*s+1) → T1=10-2c K2=1 K3=102 τ1=1c T2=1c T3=102c
НУЖНО ВСТАВИТЬ РИСУНОК!!!!
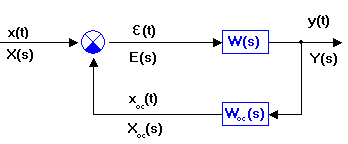
4.2 Цепь с местной обратной связью Цепь с местной обратной связью имеет следующий структурный вид:
причем сравнивающее устройство
если отрицательная обратная связь
если положительная обратная связь
Рассогласование ε (t) = x (t)- xос (t) => Выполним преобразования, “обойдя” структуру по контуру => Необходимо получить Wэкв (s) = Y (s)/ X (s), т.е. =>
↓
=> Y (s) = E (s)* W (s) = [ X (s) - Xoc (s)]* W (s) = [ X (s) - Y (s)* Woc (s)]* W (s) => [ 1+ Woc (s) *W (s)] *Y (s) = X (s) *W (s) => Wэкв (s) = Y (s)/ X (s) = W (s)/(1+ Woc (s) *W (s)) (4.13) − Эквивалентная передаточная функция для отрицательной обратной связи.
Если цепь с положительной обратной связью, то => ε (t) = x (t) + xос (t) => опуская преобразования => Wэкв (s) = Y (s) /X (s) = W (s)/(1- Woc (s) *W (s)) (4.14) Wэкв (s) = Y (s) /X (s) = W (s)/(1 ± Woc (s) *W (s)), (4.15) где знак “+” - для отрицательной обратной связи знак “−” - для положительной обратной связи
В САР почти всегда используется отрицательная обратная связь, т.е. знак “+”. Если звенья с передаточными функциями W(s) и Woc – позиционные, то Кэкв= К / (1± Кос*К) (4.16) Если обратная связь единичная, т.е. Woc = ±1, то Wэкв = W (s)/(1 ± W (s)) (4.17) В теории управления техническими системами единичную обратную связь называют, зачастую, жесткой обратной связью. =>
Формула (4.2.5) – соответствует замене цепи с местной обратной связью на эквивалентное звено.
4.2.1. Замена звена с местной обратной связью на единичную Существуют два способа замены, рассмотрим их последовательно: Ый способ Исходная САР
Эквивалентная САР
Wисх (s)= W (s)/(1+ Wос (s) *W (s)) Wэкв = [(W (s) *Wос (s)/(1+ Wос (s)* W (s))]* Z (s) Z (s)= 1 / Wос (s) (4.18) Ой способ Исходная САР
Эквивалентная САР
Wэкв = [(W (s)* Z (s)/(1+ Z (s) *W (s))] = W (s)/(1 + Wос (s) *W (s)) => Z (s)[ 1+ Wос (s)* W (s)] = 1+ Z (s)* W (s)) => Z (s)[ 1−W (s) + Wос (s)* W (s)] = 1=> Z (s) = 1 /[ 1−W (s) + Wос (s) *W (s)] (4.19)
4.3. Перенос места обратной связи “вперед” или “назад” а) вперед Исходная САР
Эквивалентная САР
Wисх (s) = W1 (s) *W2 (s)/(1+ Wос (s) *W1 (s)) Wэкв = W1 (s) *W2 (s)/(1+ Wос (s) *W1 (s) W2 (s) *Z (s)) => Z (s) = 1/ W2 (s) (4.20)
б) назад Исходная САР
Эквивалентная САР
Wисх (s) = W1 (s)* W2 (s)/(1+ Wос (s)* W1 (s) *W2 (s)) Wэкв = W1 (s) *W2 (s)/(1+ Wос (s)* W1 (s) * Z (s)) Z (s) = W2 (s) (4.21)
4.4 Перенос точек суммирования “вперед” или “назад” а) вперед Исходная схемаЭквивалентная схема
Данные рисунки не требуют дополнительных комментариев
б) назад
Исходная схемаЭквивалентная схема
Данные рисунки, также не требуют дополнительных комментариев Иногда этот прием называется “перенос внешнего воздействия” => Если считать f(t) ≡ x2(t), то это естественно!!!
4.5. Перенос точек ветвления сигнала “вперед” или “назад”
а) вперед Исходная схемаЭквивалентная схема
б) назад Исходная схемаЭквивалентная схема
Пример: Преобразовать структурную схему САР привести к единичной главной обратной связи.
Привести к виду
Этапы преобразований: 1. W1+W2 =W9 2. W4,W5 => W10 =W4 /(1+W4*W5) 3. W9, W3, W10, W6 => W11 = W9*W3*W10*W6 =>
= W* /(1+W*)=> W**W7*W11+ W11*W7 = W* + W**W8*W11 W7*W11 = W* *[ 1+W8*W11 − W11*W7 ]=> W* (s) = W11*W7 /(1+ W11 (W8 − W7))
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 966; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.74.227 (0.418 с.) |
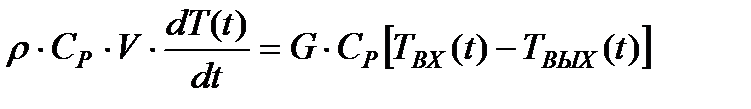 (3.3.1)
(3.3.1)


 = нулю => Tвх(0) = Tвых(0) = T0 (т.к. нет теплообмена). (3.3.2)
= нулю => Tвх(0) = Tвых(0) = T0 (т.к. нет теплообмена). (3.3.2) вх =
вх = 


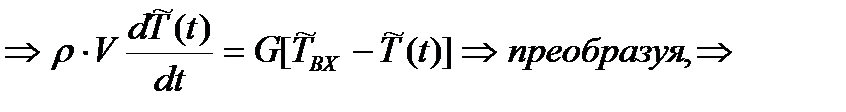
 (3.3.3)
(3.3.3) – аналог y’(t);
– аналог y’(t); – аналог y(t);
– аналог y(t);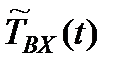 – аналог x(t).
– аналог x(t).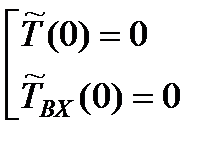


 уравнение динамики в виде ОДУ (3.3.4)
уравнение динамики в виде ОДУ (3.3.4) Y(s);
Y(s); (3.3.6)
(3.3.6) (3.3.7)
(3.3.7) =>
=> анализируя поведение u(ω) и v(ω) =>
анализируя поведение u(ω) и v(ω) =>
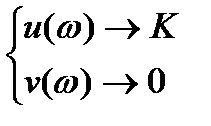

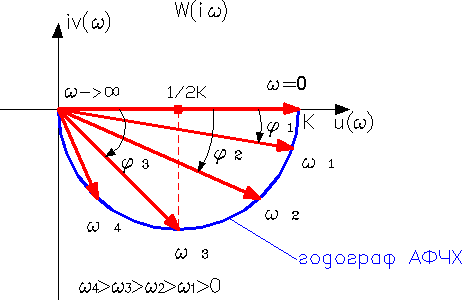
 , причем “легко видеть”, что ω3 =.
, причем “легко видеть”, что ω3 =. 

 (3.3.9)
(3.3.9)
 (3.3.10)
(3.3.10)
 =>
=>
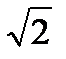 раз => А(ωсопр) =
раз => А(ωсопр) =  .
. (если К>>1)
(если К>>1) => если K≥1
=> если K≥1 => см. пример в разделе 2 =>
=> см. пример в разделе 2 => => дифференцируя по времени => получаем весовую функцию ω(t)
=> дифференцируя по времени => получаем весовую функцию ω(t) => множитель 1 (t) обеспечивает = 0 при t ≤ 0
=> множитель 1 (t) обеспечивает = 0 при t ≤ 0


 ,
, − “объемный” коэффициент теплоотдачи;
− “объемный” коэффициент теплоотдачи;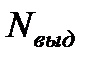 − выделяющаяся энергии (~Σf∙Φ(t)), где Σf [], Φ(t) [];
− выделяющаяся энергии (~Σf∙Φ(t)), где Σf [], Φ(t) []; (3.4.1)
(3.4.1) (3.4.2)
(3.4.2)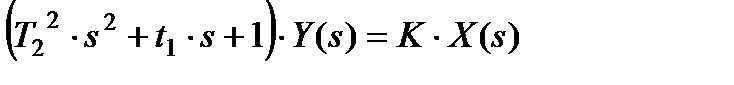 (3.4.3)
(3.4.3) (3.4.4)
(3.4.4)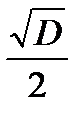 ; T4=
; T4= 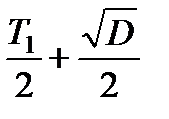 ;
;
 (3.4.5)
(3.4.5) ) и
) и  , получаем =>
, получаем =>
 (3.4.6)
(3.4.6)

 =>
=> (3.4.7)
(3.4.7)

 следует заметить, что для ω є {ω1, ω2, ω3, ω4} в формуле j = 0, а для ω = ω5; ω = ω6 => j = +1.
следует заметить, что для ω є {ω1, ω2, ω3, ω4} в формуле j = 0, а для ω = ω5; ω = ω6 => j = +1. (3.4.8)
(3.4.8) (3.4.9)
(3.4.9)

 − звено близко к идеальному усилительному звену => W(s) ≈ K
− звено близко к идеальному усилительному звену => W(s) ≈ K − звено близко к идеальному интегрирующему звену W(s) ≈ K/Ts
− звено близко к идеальному интегрирующему звену W(s) ≈ K/Ts − звено близко к дважды интегрирующему звену (W(s) ≈ K/T2s2)
− звено близко к дважды интегрирующему звену (W(s) ≈ K/T2s2)
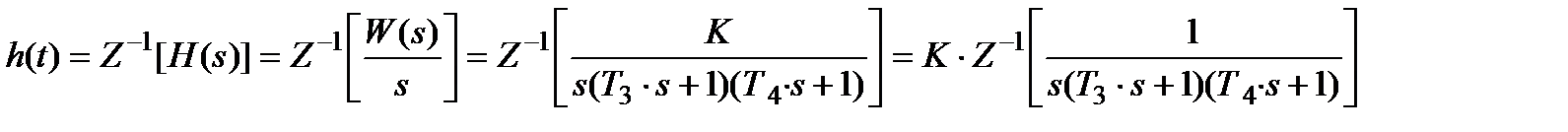 => по формуле Хэвисайда =>
=> по формуле Хэвисайда =>  (3.4.10)
(3.4.10) (3.4.11)
(3.4.11)


 =>
=> 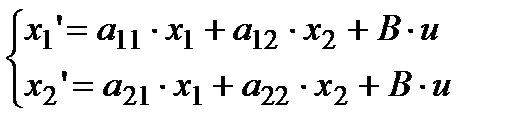 =>
=> .
. 3.5 КОЛЕБАТЕЛЬНОЕ ЗВЕНО
3.5 КОЛЕБАТЕЛЬНОЕ ЗВЕНО (3.5.1)
(3.5.1) (3.5.2)
(3.5.2) − уравнение динамики в изображениях Лапласа.
− уравнение динамики в изображениях Лапласа.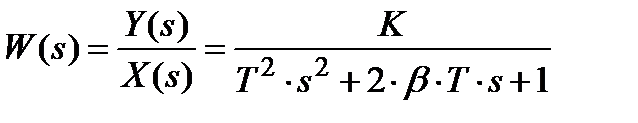 (3.5.3)
(3.5.3)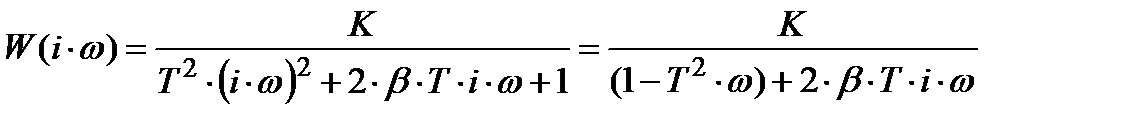 (3.5.6)
(3.5.6) (3.5.7)
(3.5.7)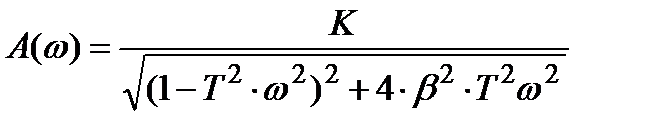 (3.5.8)
(3.5.8)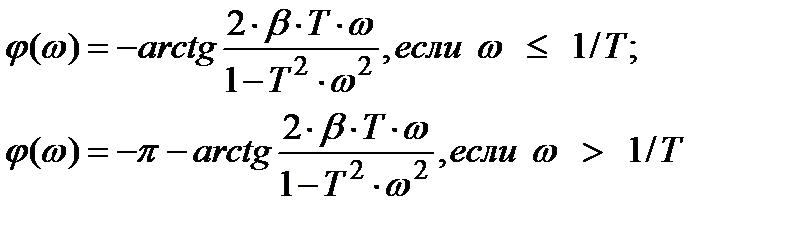 (3.5.9)
(3.5.9)
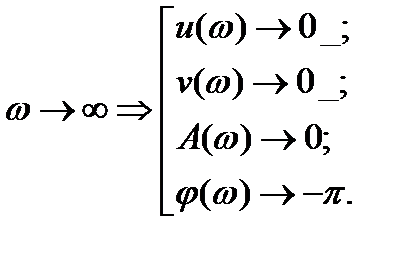
 =>
=>  (3.5.10)
(3.5.10)
 − A(ω) имеет max, если β >
− A(ω) имеет max, если β > 
 (3.5.11)
(3.5.11)

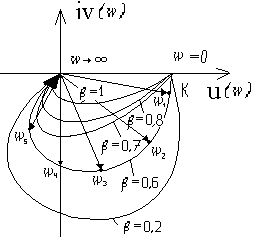
 , где ω0 − частота свободных колебаний, имеющим место в консервативном звене со следующим уравнением динамики:
, где ω0 − частота свободных колебаний, имеющим место в консервативном звене со следующим уравнением динамики: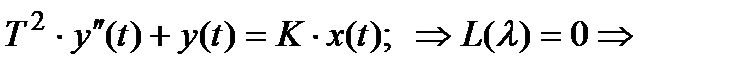


 в выражение для Lm(ω) =>
в выражение для Lm(ω) => 
 (3.5.12)
(3.5.12)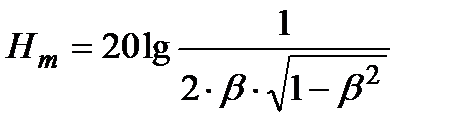 (3.5.13)
(3.5.13)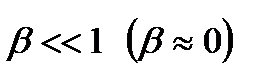 , то в упрощенных расчетах величину превышения Hm можно оценить, как:
, то в упрощенных расчетах величину превышения Hm можно оценить, как: (3.5.14)
(3.5.14)
 воспользуемся формулой Хэвисайда.
воспользуемся формулой Хэвисайда.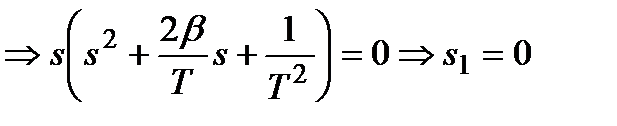
 т.к. нет повторяющихся полюсов, т.е. Kj = 1 =>
т.к. нет повторяющихся полюсов, т.е. Kj = 1 => (3.5.15)
(3.5.15)
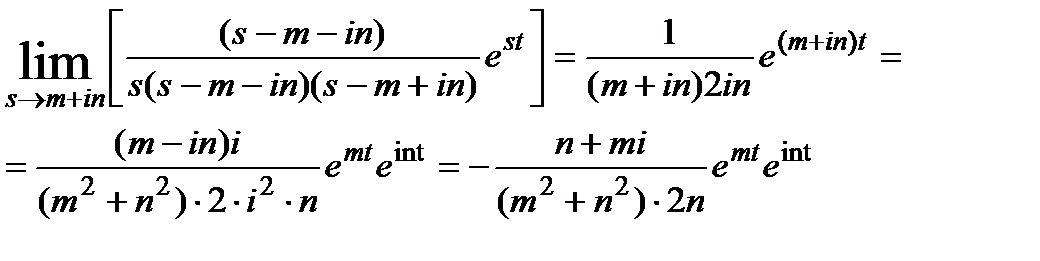




 подставляя все составляющие в формулу (3.5.15) =>
подставляя все составляющие в формулу (3.5.15) =>
 (3.5.16)
(3.5.16)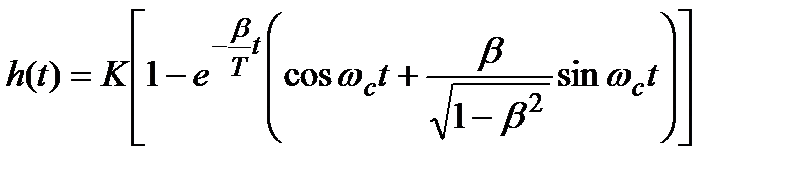 (3.5.16.а)
(3.5.16.а) называется частотой собственных колебаний (0 < β < 1).
называется частотой собственных колебаний (0 < β < 1).

 .
. т.е. собственных колебаний в звене нет, т.е. процесс без колебательный.
т.е. собственных колебаний в звене нет, т.е. процесс без колебательный.
 (3.5.17)
(3.5.17)
 возникают “трудности” со вторым слагаемым в круглых скобках формулы (3.5.16) => раскрываем неопределенность типа
возникают “трудности” со вторым слагаемым в круглых скобках формулы (3.5.16) => раскрываем неопределенность типа 

 (3.5.18)
(3.5.18)



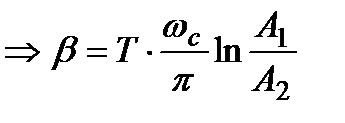 − необходимо доказать (вывести) эту формулу!!!!!
− необходимо доказать (вывести) эту формулу!!!!!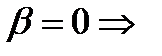
 (3.5.19)
(3.5.19)

 (3.5.20)
(3.5.20)

 (3.5.21)
(3.5.21)
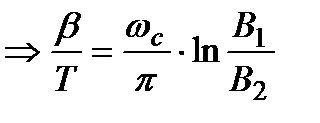



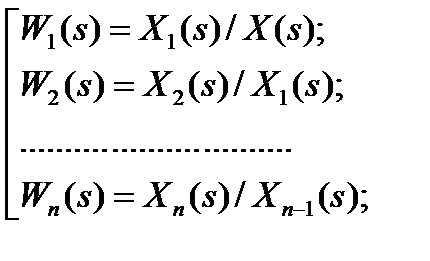
 — Эквивалентная передаточная функция. (4.1)
— Эквивалентная передаточная функция. (4.1) (4.2)
(4.2) (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5)



 (4.6)
(4.6) (4.7)
(4.7) (4. 8)
(4. 8) (4. 9)
(4. 9) (4. 11)
(4. 11) ; wэкв (t)=
; wэкв (t)=  (4. 12)
(4. 12)