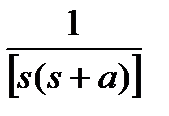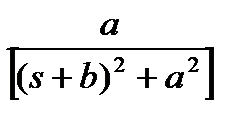Свойство запаздывания (теорема запаздывания)

 

Пусть известно преобразование f(t) F(s), а - неизвестно.

 

 

Рисунок 2.18 – Иллюстрация переходного процесса с запаздыванием

 

 

(2.6.4)

 

 

Свойство смещения в комплексной плоскости

Пусть f(t) F(s) - известно, а - неизвестно.Þ Опуская выкладки (хотя они и неложные), имеем Þ

 

(2.6.5)

 

 

Первая предельная теорема

 

Пусть f(t) F(s) - известно, а также - существует Þ

 

(2.6.6)

 

s

0 t

 

Это означает, что оси «t» и «s» формально направлены в противоположные стороны, т.е. чем больше t, тем меньше s и наоборот.

 

Вторая предельная теорема

Пусть f(t) F(s) - известно Þ тогда

 

(2.6.7)

 

 

2.7. Способы нахождения обратных преобразований Лапласа

по известному изображению

 

Вычисление оригиналов по известному (данному) изображению можно выполнить:

- по соответствующим таблицам преобразований Лапласа;

- по формулам Хэвисайда;

- разложением на элементарные дроби;

- и другие способы.

В справочниках по «Математике» приводятся довольно обширные таблицы, по которым можно найти оригиналы большинства изображений.

Однако, нередко бывают и случаи, когда необходимое преобразование отсутствует в таблицах Þ В этом случае используются различные специальные способы Þ

Если изображение F(s) можно представить в виде отношения полиномов по степеням «s», то наиболее общим и эффективным способом поиска оригинала является формула Хэвисайда. Þ если

где D₁(s) и D₀(s) – полиномы по степеням «s».

 

, (2.7.1)

 

где s_j – полюса изображения, т.е. те значения «s» при которых полином D₀(s) обращается в ноль;

k_j – кратность j – го полюса

Если уравнение D₀(s)=0 имеет n различных корней, то это означает что полюса F(s) имеют кратность, равную единице, т.е. нет повторяющихся полюсов.

Необходимо отметить, что использование формулы (2.7.1) будет корректно только в том случае, когда степень полинома D₀(s) выше степени полинома D₁(s). Если степени равны, то необходимо выделить целую часть (разделив «в столбик» полиномы) и чисто дробную часть, после чего для чисто дробной части корректна формула (2.7.1).

В качестве иллюстрации возможностей формулы Хэвисайда рассмотрим следующий пример:

Пример 1. Найти оригинал от изображения F(s) Þ

Þ ???

В данном примере полином D₁ выродился в полином нулевой степени, т.е.

D₁ = const = A.

Легко видеть, что полином D₀ = s²(T×S + 1) имеет полюса:

Þ т.е. два полюса совпадают Þ к₁ = 2.

Таблица основных преобразований Лапласа.

	Наименование функции	Оригинал	Изображение
	Единичная импульсная ф-ция	d(t)
	Единичное ступенчатое воздействие	1(t)	1 /s
	Неединичные импульсное и ступенчатое воздействия	a× d(t); a× 1(t)	a; a/s
	Экспонента	e ^–a t × 1(t)
	Степенная функция	t^n
	Синусоида	sin(at)
	Косинусоида	cos(at)× 1(t)
	Смещенная экспонента
	Затухающая синусоида
	Затухающая косинусоида