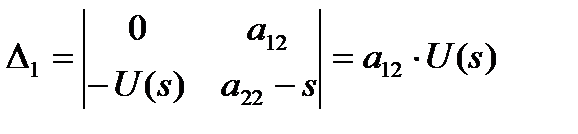Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые способы нахождения оригинала по известному изображению
Используем формулы разложения в ряды на элементарные различные дроби. Наиболее общей является формула Хэвисайда для нахождения оригиналов следующего вида:
кj – кратность полюсов Û Корни уравнения из полинома D0 – полюса (D0) Корни уравнения из полинома D1 – нули (D1). Если все корни разные, кj = 1; если корни кратные (i равных), то кj = 2; если кj = 1, то производной (!) нет. Пример: предположим изображение некоторого неизвестного процесса
Найдем полюса:
f(t)
arctgA
t Разложение на элементарные дроби.
Если корни уравнения
где
Используя свойство линейности преобразований Лапласа, мы можем найти как сумму преобразований:
Если полюса совпадают, то формула (*) несколько изменится. Пример: Имеем известное изображение:
Разложение на элементарные дроби:
Используя метод неопределенных коэффициентов, приведем полученное выражение к общему знаменателю:
f(t)
(перегиб)
t 0 4
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
x (t) САР (звено) y (t) X (s) Предположим, что уравнение динамики имеет вид:
где
Найдем изображения
Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:
Т.к. начальные условия нулевые Þ Если н.у. не нулевые Þ При нулевых н.у.
Передаточной функцией САР (звена) называется отношение изображений выходного воздействия к входному при нулевых н.у.
После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.
Пример:
x (t) Звено y (t)
Предположим, что звено имеет уравнение динамики:
ступенчатое воздействие.
y(t)
0.63k t T
2.10. Весовая и переходная функции звена (системы).
Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.
d (t) Звено y (t) = W (t)
Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.
1 (t) y (t) = h (t) Звено
Весовая функция
x(t) = d (t) y(t) º w(t) x(t) W(s) пл = 1 w(t)
t Переходная функция h(t) x(t) = 1(t) y(t) º h(t) x(t) W(s) 1
t Учитывая, что
d (t) w(t) W(s) X(s) = 1 Y(s) º W(s)
Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.
x(t) º 1(t) y(t) º h(t) W(s) X(s) = 1/s Y(s) º H(s)
H(s) – изображение h(t), т.е.
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. x(t) y(t) =? W(s) X(s) Y(s) =?
На вход системы поступает произвольное воздействие x(t) (заранее известное). Найти:
где х – нелинейное действие. Символически данное соотношение записывается:
Можно решить с помощью формулы Дюамеля-Карсона:
где t - вспомогательное время интегрирования. Если
Заменяя в формуле Дюамеля-Карсона верхний предел t на ¥, получим:
Существуют стандартные подпрограммы на ЭВМ для расчета свертки. Найдем процесс по переходной функции:
x (t) y(t) =? W(s) X(s) Y(s) =?
Запишем в изображениях связь между входом и выходом:
- формула для определения
Mетод переменных состояния.
u 1 W(s) m CAP p
Система имеет много передаточных функций: количество ТХР. Поэтому для таких многомерных систем удобно другое математическое описание.
u1(t) x 1 (t) y1(t) u2(t) x2(t) y2(t)
um(t) xn(t) yp(t)
Между «половинами» существуют внутренние переменные Обычно
где
Собственная матрица системы однозначно определяет динамические свойства системы:
первая система представляет собой систему ОДУ в обыкновенной форме Коши, вторая часть - система уравнений, описывающих выход. ОДУ в форме Коши подразумевают наличие начальных условий. В нашем случае почти всегда все элементы матрицы D будут нулевыми Þ D = 0. Такое описание системы позволяет с одной стороны стандартным образом описывать стандартные системы, используя богатое программное обеспечение, с другой стороны для простых систем, описанных в переменных «вход-выход», переход к описанию в переменных состояния зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени. Поэтому в дальнейшем мы и будем использовать подобное описание.
2.12. Переход от описания переменных «вход-выход» к переменным состояния и обратно
Рассмотрим несколько вариантов перехода. Переход зависит от правой части:
2.12.1. Правая часть содержит только b0 u(t) Допустим, что:
Введем новую переменную х1. Первое уравнение системы:
2.12.2. Правая часть общего вида
Сделаем преобразования: перейдем к уравнениям динамики в изображениях:
где Разделим все уравнение (*) на полиномы
получим вектор переменных состояния Þ Найдем теперь регулируемую величину: Рассмотрим: Перейдем к оригиналам:
Пример: u(t) y(t) W(s) U(s) Y(s)
Необходимо свести задачу к нормальной форме Коши.
Разделим левую и правую части на
Перейдем от изображений к оригиналам:
первое матричное уравнение:
Þ Рассмотрим:
Получили второе уравнение матричной системы:
Обратная задача
Цель: Имея описание системы в переменных состояния, перейти к описанию в переменных «вход-выход». x1
x2 u y xn
um(t) yp(t) Wp,m(s)
Существует несколько алгоритмов, которые позволяют рассчитать передаточную функцию: 1. Алгоритм Фадеевой 2. 3.
индексы «3» - для 3-ей управляемой величины; «2» - по 2-му управляющему воздействию.
Пример: Имеем:
Введем переменные:
u(t) W1,1(s) y(t)º x1(t)
x1 y1(t) u(t) x2 y2(t)
По определению Т.к. Используя преобразования Лапласа, получим:
Подставим соотношения в систему уравнений Þ
Система 2-х линейной алгебраический уравнений:
Система:
Вспомогательные определители системы:
Более предпочтительно использование в знаменателе собственных чисел (см. далее).
|
|||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.18.48 (0.141 с.) |
 где D0 и D1 – некоторые полиномы по степеням «s». Например:
где D0 и D1 – некоторые полиномы по степеням «s». Например: , тогда для нахождения оригинала $:
, тогда для нахождения оригинала $: ,
, - значение полюсов;
- значение полюсов;
 ;
;  ?
? ;
; 
 Þ
Þ  ;
;  ;
; Þ
Þ  ;
;  Þ
Þ  ; Þ
; Þ 
 Þ
Þ 


 различны, т.е. все разные Þ
различны, т.е. все разные Þ (*)
(*) - корни уравнения;
- корни уравнения;  - остаточный член (не разлагается на элементарные действительные дроби);
- остаточный член (не разлагается на элементарные действительные дроби);





 - оригинал: при условиях
- оригинал: при условиях 

 Þ
Þ


 Вычтем из второго уравнения первое и получим:
Вычтем из второго уравнения первое и получим:  Þ
Þ Þ
Þ


 и
и  - постоянные времени;
- постоянные времени; - коэффициент усиления.
- коэффициент усиления.










 Þ
Þ 



 - изображение выхода к изображению входа.
- изображение выхода к изображению входа. , н.у. нулевые:
, н.у. нулевые:
 - подставим все это в уравнение динамики Þ
- подставим все это в уравнение динамики Þ - уравнение динамики в изображениях
- уравнение динамики в изображениях



 - обратное преобразование Лапласа
- обратное преобразование Лапласа

 если известны
если известны  и
и 
 - связь между входным и выходным воздействиями.
- связь между входным и выходным воздействиями.
 где «*» - знак свертки.
где «*» - знак свертки.
 < 0, то
< 0, то 
 ,
, ;
; 

 ,
, Справедлива только при нулевых н.у., когда добавка равна нулю.
Справедлива только при нулевых н.у., когда добавка равна нулю. , для каждой из которых можно записать линейное ОДУ первой степени.
, для каждой из которых можно записать линейное ОДУ первой степени. . В матричной форме эта система записывается в виде:
. В матричной форме эта система записывается в виде: ,
,
 - вектор столбец производных переменных состояния;
- вектор столбец производных переменных состояния;
 - вектор столбец переменных состояния;
- вектор столбец переменных состояния; - вектор выхода;
- вектор выхода;  - вектор входа (или вектор управления);
- вектор входа (или вектор управления);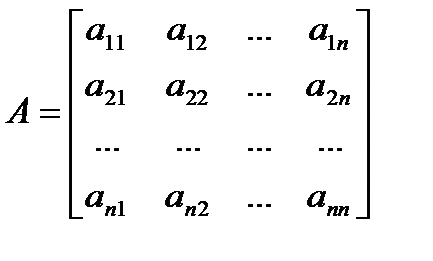 – собственная матрица системы
– собственная матрица системы  ;
; - постоянные коэффициенты;
- постоянные коэффициенты; – матрица входа
– матрица входа  ;
;  - какие-то постоянные коэффициенты;
- какие-то постоянные коэффициенты; – матрица выхода
– матрица выхода  ;
; – матрица обхода или дополнительная матрица выхода
– матрица обхода или дополнительная матрица выхода  ;
; -
-


 .
. ;
;  ;
;  ;
;  .
.
 Начальные условия нулевые.
Начальные условия нулевые.
 , (*)
, (*) ,
,  - полиномы.
- полиномы. - какая-то комплексная величина (отношение двух комплексных величин).
- какая-то комплексная величина (отношение двух комплексных величин). ,
,  - изображение какой-то переменной
- изображение какой-то переменной 
 и преобразуем:
и преобразуем:  , где
, где  - какой-то дифференциальный оператор.
- какой-то дифференциальный оператор.
 + н.у. Þ получится задача Коши Þ
+ н.у. Þ получится задача Коши Þ .
. Þ
Þ 



 н.у. нулевые.
н.у. нулевые.
 ;
; Þ
Þ


 ,
,

 - н.у.. Получаем задачу Коши для ОДУ. Þ
- н.у.. Получаем задачу Коши для ОДУ. Þ - найдены.
- найдены. ;
; .
. ;
;  ;
;  .
.
 - одно конкретное управляющее воздействие и соответствующая регулируемая величина.
- одно конкретное управляющее воздействие и соответствующая регулируемая величина.
 - алгоритм
- алгоритм - алгоритм (крайне редко пользующийся).
- алгоритм (крайне редко пользующийся). ,
, - одна и та же функция, меняющая только числитель.
- одна и та же функция, меняющая только числитель.

 ;
; 
 ,
, ,
,  ,
, Þ
Þ 






 .
. ;
;  - правило Крамера
- правило Крамера