
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности. Вывод передаточной функции, переходной и весовой функций.Содержание книги
Поиск на нашем сайте
Дадим краткое пояснение ряда терминов, используемых в заглавии данного подраздела: 1. «Точечный» Þ означает, что хотя реактор и представляет собой пространственный объект, тем не менее кинетика (изменение во времени) нейтронов может быть условно описана «материальной точкой», имеющей такие же свойства (в динамическом плане), что и реальный реактор Þ т.е. пространственные размеры (диаметр, высота) не учитываются. Такое допущение вполне корректно для большинства реакторов: реакторы малой энергетики, лодочные (транспортные) реакторы и с некоторым допущением и большие реакторы (ВВЭР, PWR, BWR, HTGR и т.д.). 2. «Нулевой» Þ означает, что либо мощность (энерговыделение) реактора незначительна и поэтому ее изменение не влияет на нейтронно-физические характеристики, либо хотя мощность и немала, но внутренние обратные связи (обусловленные различными эффектами реактивности, например, мощностным, температурным, плотностным и т.д. эффектами) не учитываются. 3. «Кинетика» Þ практически тождественно слову «динамика», но в теории управления ядерными реакторами принято называть нестационарные режимы в балансе нейтронов в реакторе без обратных связей термином кинетика. Если учитываются обратные связи (внутренние и внешние), то тогда используется термин динамика ядерного реактора. Прежде чем выводить уравнения кинетики нейтронов сделаем еще ряд допущений (к вышеописанным 1 и 2 допущениям): ¨ будем считать, что на кинетику влияют в основном тепловые нейтроны Þ т.е. одногрупповое приближение; ¨ будем считать, что запаздывающие нейтроны могут быть описаны 1-ой эффективной группой, хотя обычно запаздывающие нейтроны подразделяются на 6 групп со своими постоянными распада ядер-предшественников запаздывающих нейтронов.
осколок запаздывающий нейтрон 0 n 1 ядро мгновенные 2¸ 3 нейтрона U 235 Осколок – запаздывающий 0 n 1
Из курса «ФЯР» известно, что доля мгновенных нейтронов, рождаемых от деления ядра, составляет > 99%, т.е. доля запаздывающих нейтронов составляет» 0.25¸0.7% от общего числа рожденных нейтронов. Запаздывающие нейтроны вылетают из осколков через относительно большое время после деления ядра: обычно от сотых долей секунды до сотен секунд, в то время как мгновенные нейтроны через» 1 мсек (или еще быстрее, например, через 10¸100 мксек). Из курса «ФЯР» известно следующее нестандартное уравнение баланса нейтронов в реакторе в одногрупповом (по энергии нейтронов) приближении:
где Пмгн =
v(t) – средняя скорость нейтрона в реакторе (в одногрупповом приближении). C(t) – концентрация ядер-предшественников запаздывающих нейтронов, После подстановки составляющих в систему (2.13.1) Þ
Необходимо подчеркнуть, что если Кэфф = 1, то доли:
Опуская подробные выкладки, но тем не менее вводя новые обозначения:
Примем для простоты, что внешнего источника нет Þ
Выполняя аналогичные преобразования для 2-го уравнения системы (2.13.2), имеем:
Þ окончательно:
(2.13.4)
Объединяя уравнения (2.13.3) и (2.13.4) в систему, получаем систему уравнений кинетики нейтронов:
или
Учитывая, что Систему уравнений (2.13.5) - систему 2-го порядка – можно представить структурно так: r(t) n(t) реактор Þ c(t) Причем 2-е уравнение (2.13.5) – линейное, а 1-е – нелинейное, т.к. есть член ~ Найдем условия статики критичного реактора (стационарного состояния): Если Þ где n0 – равновесная плотность нейтронов; с0 – равновесная концентрация ядер-предшественников запаздывающих нейтронов Þ
Þ
Дальнейшие преобразования выполним со следующей целью: 1. Перейдем к безразмерным переменным; 2. Линеаризуем 1-е уравнение системы (2.13.5); 3. Получить передаточную функцию, описывающую кинетику нейтронов в переменных «вход-выход». 4. Получить систему уравнений в форме Коши. Þ Введем новые безразмерные переменные:
Учитывая, что Подставляя новые переменные
- это система уравнений в форме Коши, т.е. в переменных состояния. Таким образом получена линеаризованная система уравнений для безразмерных переменных Приведем описание кинетики нейтронов к стандартному виду в переменных «вход-выход» Þ
r(t) Реактор способами
1-ый способ: Дифференцируя 1-е уравнение системы (2.13.8) Þ
Перенося слагаемые, содержащие
Þ используя преобразования Лапласа Þ
Уравнение кинетики в изображениях:
- передаточная функция «точечного» реактора с «нулевой» мощностью. 2-ой способ: Используя систему (2.13.8) Þ
Þ Þ
Þ
Хотя традиционной переходной характеристикой любого (почти любого) звена, объекта САР и т.д. является переходная функция h(t) (реакция на 1(t)), в данном случае такое воздействие по реактивности недопустимо, т.к. величина
Если сумма 1-го и 3-го слагаемых отрицательна, то «разгон» реактора идет за счет 2-го слагаемого Þ для которого характерные времена определяются из 2-го уравнения системы Þ характерное время » 1/l» 10 сек. Если Поэтому рассмотрим реакцию на ступенчатое воздействие:
Þ примем, что
Нахождение оригинала выполним новым способом, Þ разложением изображения на элементарные дроби Þ
тогда окончательно получаем:
или
Из выражения для
при при
|
||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 839; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 (2.13.1)
(2.13.1) - порождение мгновенных нейтронов первичными нейтронами;
- порождение мгновенных нейтронов первичными нейтронами; - порождение запаздывающих нейтронов за счет распада ядер-предшественников з.н;
- порождение запаздывающих нейтронов за счет распада ядер-предшественников з.н; - поглощение нейтронов;
- поглощение нейтронов; - утечка нейтронов из реактора за счет диффузии, где D – коэффициент диффузии,
- утечка нейтронов из реактора за счет диффузии, где D – коэффициент диффузии,  - геометрический фактор (параметр).
- геометрический фактор (параметр). - внешний источник нейтронов;
- внешний источник нейтронов; - порождение ядер – предшественников запаздывающих нейтронов;
- порождение ядер – предшественников запаздывающих нейтронов; - распад ядер – предшественников запаздывающих нейтронов.;
- распад ядер – предшественников запаздывающих нейтронов.; - плотность нейтронов,
- плотность нейтронов,  или
или  ;
; - поток нейтронов,
- поток нейтронов,  или
или  ;
; (2.13.2)
(2.13.2) - доля мгновенных нейтронов во втором поколении;
- доля мгновенных нейтронов во втором поколении;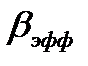 - доля запаздывающих нейтронов во втором поколении;
- доля запаздывающих нейтронов во втором поколении; - эффективный коэффициент размножения;
- эффективный коэффициент размножения;
 - реактивность (
- реактивность ( » 1);
» 1); - время жизни мгновенных нейтронов без учета утечки из реактора;
- время жизни мгновенных нейтронов без учета утечки из реактора; - время жизни мгновенных нейтронов с учетом утечки (
- время жизни мгновенных нейтронов с учетом утечки ( >
>  ;
;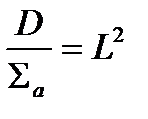 - квадрат длины диффузии нейтрона;
- квадрат длины диффузии нейтрона; . Преобразим 1-е уравнение системы (2.13.2) Þ
. Преобразим 1-е уравнение системы (2.13.2) Þ Þ окончательно:
Þ окончательно: (2.13.3)
(2.13.3)

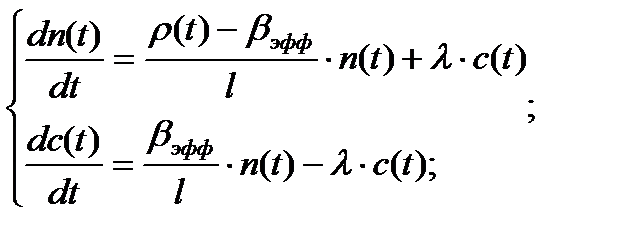 (2.13.5)
(2.13.5) (2.13.6)
(2.13.6) » 1, то вместо «точной» системы (2.13.6) удобнее использовать «приближенную» систему (2.13.5).
» 1, то вместо «точной» системы (2.13.6) удобнее использовать «приближенную» систему (2.13.5).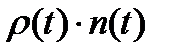 .
. или Кэфф(0) = 1!!! Þ
или Кэфф(0) = 1!!! Þ ,
, (2.13.7)
(2.13.7)

 и в стационаре
и в стационаре  ,то переменную
,то переменную  нет смысла обезразмеривать, т.к. она и так безразмерна.
нет смысла обезразмеривать, т.к. она и так безразмерна. и
и  в 1-е уравнение системы (2.13.5), получаем:
в 1-е уравнение системы (2.13.5), получаем: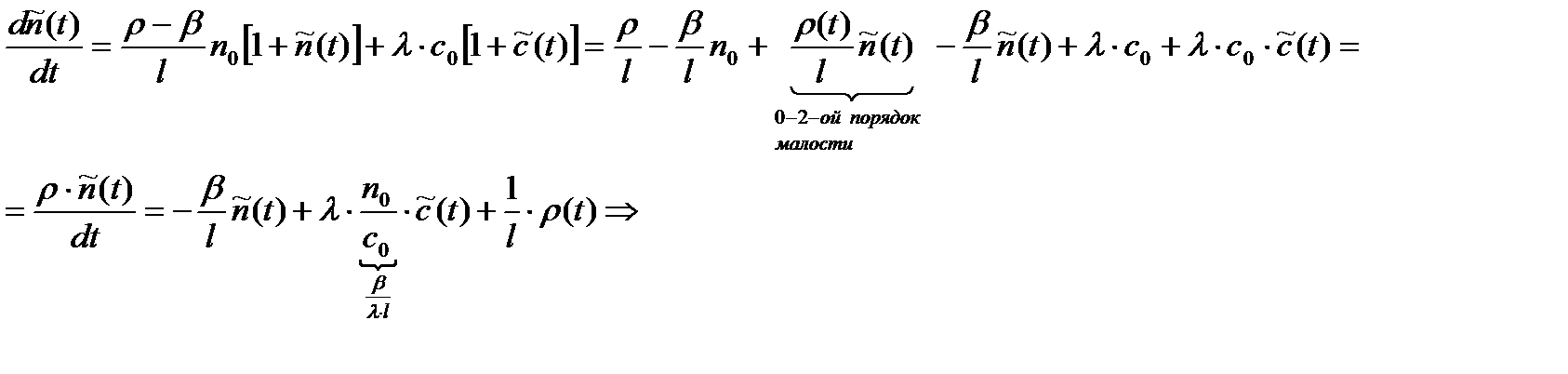
 (12.13.8)
(12.13.8) , описывающих кинетику нейтронов в реакторе.
, описывающих кинетику нейтронов в реакторе.
 Þ
Þ (2.13.9)
(2.13.9)
 Þ
Þ Þ
Þ (2.13.10)
(2.13.10)
 Þ
Þ Þ
Þ Þ
Þ
 Þ
Þ Þ
Þ Þ данное выражение совпало с выражением (2.13.10)
Þ данное выражение совпало с выражением (2.13.10) (зависит от вида ядерного топлива и типа реактора), и поэтому величина воздействия по реактивности больше, чем
(зависит от вида ядерного топлива и типа реактора), и поэтому величина воздействия по реактивности больше, чем  делает реактор критическим (точнее надкритическим) на мгновенных нейтронах, что недопустимо из соображений ядерной безопасности, т.к. таким реактором управлять практически невозможно. Þ Это особенно наглядно видно из системы уравнений (линеаризации) Þ
делает реактор критическим (точнее надкритическим) на мгновенных нейтронах, что недопустимо из соображений ядерной безопасности, т.к. таким реактором управлять практически невозможно. Þ Это особенно наглядно видно из системы уравнений (линеаризации) Þ , то разгон будет определяться, в основном, 3-им слагаемым в 1-ом уравнении Þ характерная постоянная времени
, то разгон будет определяться, в основном, 3-им слагаемым в 1-ом уравнении Þ характерная постоянная времени  , т. е. порядка 10-3 сек (и меньше), а это в технике практически мгновенно, т.е. «взрыв»!!!
, т. е. порядка 10-3 сек (и меньше), а это в технике практически мгновенно, т.е. «взрыв»!!! где
где  Þ
Þ n(t)
n(t)
 N*(s) Þ
N*(s) Þ , где
, где  - реакция на мгновенный«скачок»реактивности.
- реакция на мгновенный«скачок»реактивности.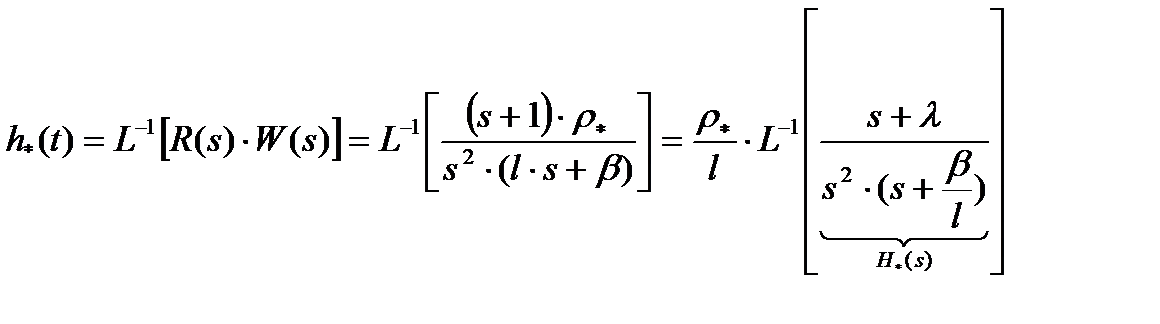 (2.13.11)
(2.13.11)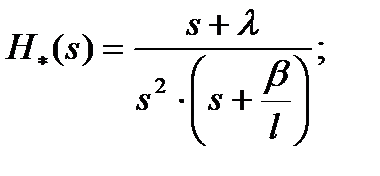 Þ
Þ  Þ
Þ Þ отсюда Þ
Þ отсюда Þ

 Þ подставляя значения А,В,С Þ при t > 0
Þ подставляя значения А,В,С Þ при t > 0
 (2.13.12)
(2.13.12) , т.к. b>>l.×l.
, т.к. b>>l.×l. Þ формула (2.13.12) Þ,т.к.
Þ формула (2.13.12) Þ,т.к. 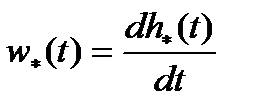 Þ
Þ

 Þ
Þ 



