
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные характеристики замкнутой САР.
Наибольшее распространение при анализе замкнутых САР имеет АФЧХ замкнутой САР по управляющему воздействию Þ
Ф(iw) = Ф(s)s = iw =
где W(i w) = Учитывая, что W(iw) = u(w) + i × u(w) - комплексное число, по аналогии имеем:
Ф (iw) = P (w) + i × Q (w), (5.3.2)
где P(w) = Re[ Ф(iw) ] и Q(w) = Im[Ф(iw)].
P (w) Q (w)
На этих рисунках представлен «примерный» вид зависимостей P (w)и Q(w) для «какой-то» замкнутой САР Þ причем P(w) - четная функция, т.е. P(w) = P(-w); Q(w) - нечетная функция, т.е. Q(w) = -Q(-w). Если известны частотные свойства разомкнутой САР, то можно определить частотные свойства замкнутой САР Þ воспользуемся показательной формой для АФЧХ Þ W (iw) = А (w)× е i j(w), где А(w) - амплитуда (модуль) и j(w) – сдвиг фазы (фаза). Подставляя это в (5.3.1), имеем Ф(iw) = Азамк(w) × е I j3(w) =
учитывая, что е – ij = cos(j) - i×sin(j) Þ
Приравнивая чисто вещественные и чисто мнимые части, имеем Þ
Задачей преобразований является Þ найти: А3(j) = f1[ A(w), j(w) ]; j3(w) = f2[ A(w), j(w) ] Þ Разделив (2) на (1) Þ tgj3(w) =
j3амкнутой(w) = arctg
где j – определяется из графика Ф(iw). Процедура получения выражения для А3(w) – сложнее Þ возведем оба уравнения системы (5.3.5) в квадрат Þ
Þ складывая эти уравнения Þ
А3(w) =
Аналогичным образом можно выразить, например, P(w) и Q(w) - характеристики замкнутой САР через u(w) и u(w) - характеристики разомкнутой САР Þ существуют номограммы Солодовникова, Никольса для определения частотных свойств замкнутой САР Þ они называются диаграммами замыкания, но в настоящее время благодаря достижениям вычислительной техники – компьютеров, эти диаграммы практически полностью потеряли свою актуальность.
6. Устойчивость линейных и линеаризованных систем автоматического регулирования (управления).
6.1. Понятие об устойчивости САР. Теоремы Ляпунова.
В теории «Управления техническими системами» общепринято понятие качество управления, состоящее из трех основных составляющих: - устойчивость САР (или запасы устойчивости); - точность САР; - качество переходного процесса. Необходимо заметить, что если не обеспечена устойчивость замкнутой САР, то говорить о точности и, тем более, о качестве переходного процесса - бессмысленно.
Поэтому понятие «устойчивость» - важнейшее понятие для САР. Приведем «механическую» аналогию понятия «устойчивость» Þ
1. 2. 3. абсолютно неустойчивое нейтральное устойчивое положение (безразличное) положение В положении 1 при отклонении шарика от нижнего положения он обязательно вернется в свое устойчивое положение (низ «воронки»). В положении 2 малейшее отклонение шара от состояния равновесия приведет к «скатыванию» его вниз; т.е. шар не вернется сам назад на вершине «горки». В положении 3 при воздействии на шар он начнет перемещаться в горизонтальном направлении и, если нет трения, то шар будет двигаться с постоянной скоростью. Если реальная замкнутая САР имеет свойства, аналогичные 1, то она «хорошая», если 2 – «совсем плохая». Þ Нужно так проектировать САР, чтобы ее свойства были похожи на 1, т.е. если какое-то возмущающее воздействие отклонит систему от равновесия, то система управления обязана вернуть техническую систему в состояние равновесия. Рассмотрим техническую систему (САР), описываемую в переменных «вход-выход»
Þ
- уравнение динамики замкнутой САР при управляющем воздействии. Учитывая, что
Û находим l. Тогда Þ
Þ возможно несколько вариантов в зависимости от значений



Анализ вышеприведенных рисунков показывает, что система может вернуться в исходное состояние, если все составляющие Jm Причем ось ординат l j устойчивости (апериодической или колебательной).
Re Таким образом, вопрос об устойчивости или неустойчивости замкнутой (и разомкнутой) САР определяется по расположению корней соответствующего характеристического уравнения:
Если все корни характеристического уравнения лежат (расположены) в левой полуплоскости – линейная (или линеаризованная) САР устойчива. Необходимо заметить, что коэффициенты уравнения
Используя приблизительно такие же рассуждения (см. выше), Ляпуновым были сформулированы 3 теоремы об устойчивости линейных САР: Þ их «суть» Þ 1. Если все корни характеристического уравнения или полюса передаточной функции САР расположены в левой полуплоскости, то линеаризованная САР обязательно вернется в исходное состояние при снятии внешнего воздействия, выведшего эту САР из состояния равновесия. Þ Следовательно САР – устойчива. 2. Если хотя бы один полюс (или корень характеристического уравнения) передаточной функции САР расположен в правой полуплоскости (при всех остальных в левой полуплоскости), линейная (линеаризованная) САР никогда не вернется в исходное (равновесное) состояние при снятии внешнего воздействия, которое вывело данную САР из исходного состояния равновесия. Þ Следовательно САР – неустойчива. 3. Если хотя бы один из полюсов передаточной функции САР (корней характеристического уравнения) находится на мнимой оси (при всех остальных в левой полуплоскости) об устойчивости линеаризованной САР ничего сказать нельзя, т.к. учет нелинейных (отброшенных) членов в динамике САР может дать любой результат (устойчива или неустойчива). Резюмируя вышесказанное, отметим, что: Наиболее простым способом определения устойчива или неустойчива САР (как замкнутая, так и разомкнутая) является решение уравнения D(s) = 0 для замкнутой САР (или L(s) = 0 для разомкнутой САР) или решение характеристического уравнения D(l) = 0 или (L(l) = 0 – для разомкнутой САР). Если САР задана в переменных состояния Þ
Þ вопрос об устойчивости САР определяется матрицей А – собственной матрицей. Если собственные числа матрицы А лежат в левой полуплоскости – САР устойчива; если хотя бы одно собственное число лежит в правой полуплоскости – линейная САР неустойчива. Собственные числа (согласно разделу «Линейная алгебра») находятся из уравнения:
где А – матрица размера Е – единичная матрица.
Это означает, что уравнение принимает вид Þ
Þ решая, находим Фактически уравнения (6.1.6) и (6.1.7) – характеристические уравнения САР. Поэтому, если САР задана в переменных состояния, то характеристический полином D(s) при задании САР в переменных «вход-выход» может быть определен как
Чисто математически задача определения устойчивости сводится к решению степенного уравнения 6.2. Необходимые условия устойчивости линейных и линеаризованных САР.
Наиболее просто необходимое условие устойчивости линейных (линеаризованных) САР формулируется для систем, записанных в переменных «вход-выход», причем оно применяется в одинаковой «редакции» как для замкнутых, так и для разомкнутых САР. Þ Это условие доказывается с использованием характеристического полинома D(s) – для замкнутых САР, или L(s) – для разомкнутых САР. Сделаем вывод на основании D(s) Þ
Разложим многочлен D(s) на элементарные линейные сомножители Þ:
(6.2.1), где Предположим, что
Þ
Подставляя Подставляя значение Подставляя значение
Þ Для систем 1-го и 2-го порядка необходимое условие является и достаточным. Но для систем, имеющих порядок Тем не менее, необходимое условие «очень удобно», т.е. если хотя бы один коэффициент в D(s) отрицателен, то однозначно – САР неустойчива. Если необходимое условие выполнено
6.3. Алгебраический критерий устойчивости Гурвица.
Как отмечалось выше, устойчивость любой САР можно определить, вычислив значение всех полюсов (или корней соответствующего характеристического уравнения). Однако далеко не все способны без компьютера (калькулятора) решить степенное уравнение выше квадратного (кубическое и т.д.). Þ Критерий Гурвица, являющийся частным случаем критерия Раусса, позволяет не решая уравнений типа D(s) = 0 или
Представим полином D(s) в измененном виде:
Дадим формулировку критерия Гурвица без доказательства: Þ

Если все Если Если Достоинством критерия Гурвица – простота алгоритма. Главным недостатком – трудно использовать для систем, имеющих порядок выше 4 без соответствующих программных средств. Поэтому используют, если Пример1: определить, устойчива или нет следующая система САР:
x(t) y(t)
Замечаем, что разомкнута САР – устойчива, т.к. она 2-го порядка и все коэффициенты знаменателя – положительны. Найдем главную передаточную функцию замкнутой САР: Þ
Пример 2: Используя критерий Гурвица, выполнить анализ устойчивости следующей САР Þ
Разомкнутая САР Þ Замкнутая САР Þ
Запишем матрицу Гурвица Þ
1. совершенно очевидно, что 0 2. найдем условие колебательной границы устойчивости Þ
Þ 3. найдем условие устойчивости САР Þ
 Þ Þ  К К
Полученный результат свидетельствует, что если Усложним задачу: предположим возможно варьировать (изменять) коэффициент усиления К и постоянную времени, например,
К Система неравенств такая же, что и выше: Þ
T2

6.4. Частотный критерий устойчивости Михайлова.
Советским ученым Михайловым в в 30-тых годах впервые был предложен оригинальный критерий оценки устойчивости САР, основанный на исследовании частотных свойств полинома
Þ такая же форма записи, что и в критерии Гурвица. Если
Þ
Совершенно очевидно, что:
если
если
Формулировка: Þ Чтобы САР (замкнутая или разомкнутая) была устойчивой, необходимо и достаточно, чтобы годограф D (i×w) при изменении w от нуля до ¥ переходил поочередно из квадранта в квадрант против часовой стрелки, совершив при этом поворот на угол
w 3
Если САР – устойчива, то вектор
Следствием частотного критерия Михайлова является перемежаемость (чередование) нулей полиномов
w
Þ Нули полиномов Если система находится на апериодической границе устойчивости (один нулевой полюс при всех остальных в левой полуплоскости), то годограф iD2(w)
Если система находится на колебательной границе устойчивости (2 чисто мнимых полюса при всех остальных в левой полуплоскости), то годограф iD2(w) Þ годограф D(iw) при некоторой частоте w = w* проходит через начало координат, «перескакивая» из w = 0 w = w* незатухающих колебаний в такой САР. Если САР неустойчива, годографы имеют вид:
Докажем ряд основных «моментов» в критерии Михайлова Þ Во-первых, представим полином
где Учитывая, что любое комплексное число типа
где
Естественно: Будем обозначать изменение фазы (аргумента) Þ
во-вторых, предположим, что САР - устойчива, т.е. все полюса Рассмотрим различные варианты полюсов, а именно: действительные, комплексные Þ 1-ый случай: Пусть Рассмотрим поведение вектора
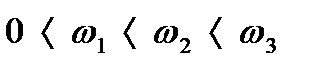 Þ естественно, что при Þ естественно, что при  , при , при 
w 1 j w 0 Re
Т.е. при изменении
2-ой случай: Пусть Рассмотрим скобку Þ iIm w®¥
w 4 очевидно Þ w 3 Þ очевидно, что при Re g2 w 1
3-ий случай: Пусть Рассмотрим скобку iIm w®¥
w 2 очевидно Þ w 1 Þ очевидно, что при
g2
Учитывая, что
Учитывая, что вещественный полюс дает
- если все полюса в левой полуплоскости, т.е. САР – устойчива. Это означает, что при изменении частоты от нуля до бесконечности, годограф Предположим, что САР – неустойчива, т.е. ряд полюсов расположен в правой полуплоскости Þ 4-ый случай: Пусть
w 1 очевидно, что -a 4
Þ Следовательно скобка Þ Рассмотрим два оставшихся случая Þ Пусть iIm
w®¥ Очевидно, что 0 <w 1 < w 2 < w 3 и т.д. w 3 что w = 0 Þ j 5 (0) = p + g 5 w 2 w ® ¥ Þ j 5 (¥) ® 0.5×p Re w 1 w 0 -i×b 5
6-ой случай: Пусть iIm w 2 w = 0 Þ j 6 (0) = p - g 5 w 1 w ® ¥ Þ j 6 (¥) ® 0.5×p Þ
w 0 -a 5 Re
Суммируя
Резюмируя вышеприведенное Þ Если САР – устойчива (все полюса в левой полуплоскости), то
Если 1 полюс расположен в правой полуплоскости (при всех остальных в левой), то:
Если в правой полуплоскости расположено L полюсов, то:
Специально необходимо отметить еще один «предельный» случай Þ бесконечного полюса (корня) Þ
Область расположения корней (полюсов)
бесконечный полюс Þ Данный случай возникает, если iIm
Re
а 0 < 0
а 0 = 0 а 0 > 0 Пример: Необходимо исследовать на устойчивость САР Þ используя критерий Михайлова
Þ
0 w 0 Þ САР – неустойчива, т.к. нет чередования нулей D 1 и D 2
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.200.143 (0.324 с.) |
 , (5.3.1)
, (5.3.1) .
. Þ
Þ , (5.3.3)
, (5.3.3) . (5.3.4)
. (5.3.4) (1) (5.3.5)
(1) (5.3.5) (2).
(2). Þ
Þ , (5.3.6 )
, (5.3.6 ) ;
; ;
;
 Þ
Þ ; (5.3.7)
; (5.3.7)
 (6.1.1)
(6.1.1) , рассмотрим составляющую
, рассмотрим составляющую  Þ решая характеристическое уравнение:
Þ решая характеристическое уравнение: (6.1.2)
(6.1.2) Þ
Þ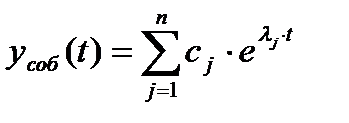 Þ (6.1.3)
Þ (6.1.3) .
.

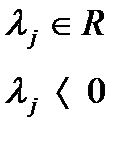



 будут стремиться к нулю. Þ Поэтому условием устойчивости является
будут стремиться к нулю. Þ Поэтому условием устойчивости является  Þ т.е. корни характеристического уравнения лежали в левой полуплоскости Þ
Þ т.е. корни характеристического уравнения лежали в левой полуплоскости Þ соответствует границам
соответствует границам (6.1.4)
(6.1.4) совпадают с коэффициентами многочлена (полинома)
совпадают с коэффициентами многочлена (полинома)  Þ следовательно
Þ следовательно  Þ полюса замкнутой САР тождественно совпадают с корнями характеристического уравнения Þ
Þ полюса замкнутой САР тождественно совпадают с корнями характеристического уравнения Þ  , где
, где  - корни характеристического уравнения;
- корни характеристического уравнения; - полюса передаточной функции замкнутой САР.
- полюса передаточной функции замкнутой САР. (6.1.5)
(6.1.5) (6.1.6)
(6.1.6) ;
; Þ
Þ (6.1.7)
(6.1.7) .
.
 или к проблеме нахождения собственных чисел матрицы А.
или к проблеме нахождения собственных чисел матрицы А.
 - полюса передаточной функции замкнутой САР.
- полюса передаточной функции замкнутой САР. , и что все полюса
, и что все полюса  расположены в левой полуплоскости: Þ
расположены в левой полуплоскости: Þ Þ
Þ - действительный полюс;
- действительный полюс; - комплексно-сопряженные полюса.
- комплексно-сопряженные полюса. );
); во вторую скобку (6.2.1) Þ
во вторую скобку (6.2.1) Þ  .
. в третью скобку (6.2.1) Þ
в третью скобку (6.2.1) Þ 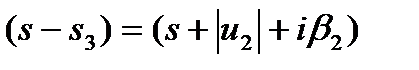 Þ перемножим эти три скобки Þ
Þ перемножим эти три скобки Þ =
=  )×[
)×[  ]×[
]×[  ]=
]= 
 Þ т.е. все слагаемые положительны, т.е. Þ подставляя и в другие скобки Þ поскольку вещественная часть всех полюсов отрицательна Þ
Þ т.е. все слагаемые положительны, т.е. Þ подставляя и в другие скобки Þ поскольку вещественная часть всех полюсов отрицательна Þ  Þ, то в выражении (6.2.1) скобки будут принимать вид типа
Þ, то в выражении (6.2.1) скобки будут принимать вид типа  , или, если перемножить 2 скобки с комплексно-сопряженными полюсами, принимать вид типа
, или, если перемножить 2 скобки с комплексно-сопряженными полюсами, принимать вид типа  Þ отсюда очевидно, что если раскрыть все скобки в (6.2.1), то, учитывая, что
Þ отсюда очевидно, что если раскрыть все скобки в (6.2.1), то, учитывая, что  , получим полином D(s), у которого все коэффициенты положительны. Это результат и составляет суть необходимого условия: необходимым условием устойчивости линейных САР является положительность всех коэффициентов в полиноме D(s) - для замкнутых САР, или в L(s) – для разомкнутых САР.
, получим полином D(s), у которого все коэффициенты положительны. Это результат и составляет суть необходимого условия: необходимым условием устойчивости линейных САР является положительность всех коэффициентов в полиноме D(s) - для замкнутых САР, или в L(s) – для разомкнутых САР. , выполнение необходимого условия невсегда является достаточным.
, выполнение необходимого условия невсегда является достаточным.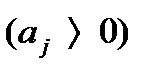 , то если
, то если 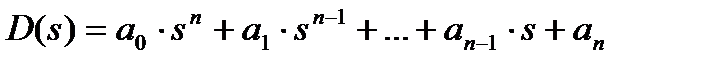 (6.3.1)
(6.3.1)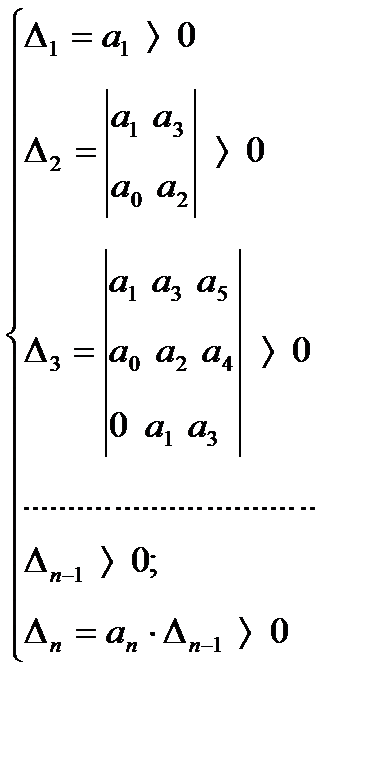
 (от
(от  до
до  ) больше (строго) нуля, то линейная САР (или линеаризованная) устойчива.
) больше (строго) нуля, то линейная САР (или линеаризованная) устойчива. , а коэффициент
, а коэффициент  , то САР находится на апериодической границе устойчивости.
, то САР находится на апериодической границе устойчивости. , а определитель
, а определитель  при значении
при значении  , то САР находится на колебательной границе устойчивости.
, то САР находится на колебательной границе устойчивости. !!!
!!!

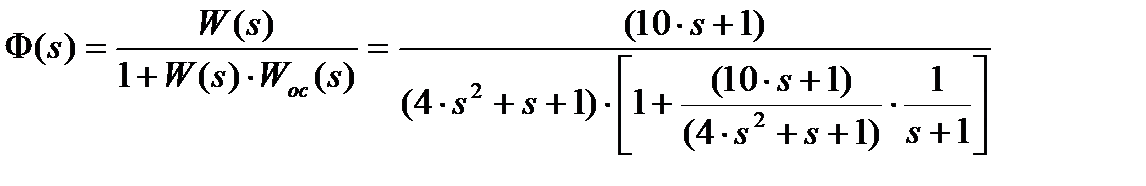 Þ
Þ
 Þ Запишем Гурвицеву матрицу Þ
Þ Запишем Гурвицеву матрицу Þ Þ САР устойчива.
Þ САР устойчива.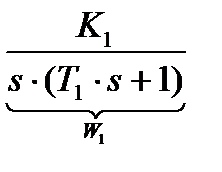



 Þ находится на границе устойчивости, т.к.
Þ находится на границе устойчивости, т.к.  !!!
!!!

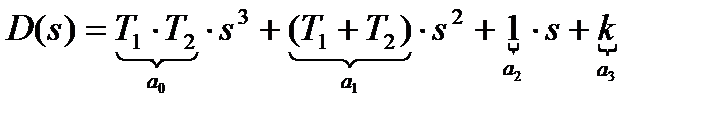 Þ
Þ Þ
Þ Þ К
Þ К !!! Þ
!!! Þ  - условие нахождения САР на колебательной границе устойчивости
- условие нахождения САР на колебательной границе устойчивости
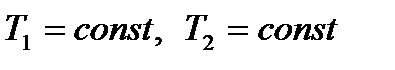 , то для того, чтобы САР была устойчивой, необходимо, чтобы
, то для того, чтобы САР была устойчивой, необходимо, чтобы  ;
; Þ т.е.
Þ т.е. Þ
Þ Þ
Þ

 при подстановке вместо
при подстановке вместо  , где
, где  !!!
!!! (6.4.1)
(6.4.1) Þ (6.4.2)
Þ (6.4.2) (6.4.3)
(6.4.3) Þ
Þ  ;
;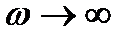 Þ
Þ 
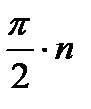 .
.



 совершает поворот на угол
совершает поворот на угол  и
и  Þ в самом деле (см. рисунок), для кривой с
Þ в самом деле (см. рисунок), для кривой с  Þ «
Þ « » Þ
» Þ
 w 2 w 3 w 4
w 2 w 3 w 4
 имеет следующий «примерный» вид:
имеет следующий «примерный» вид: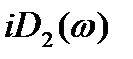

 (6.4.3)
(6.4.3)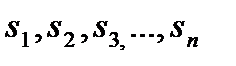 - полюса главной передаточной функции
- полюса главной передаточной функции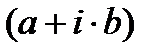 можно представить в виде:
можно представить в виде:  , где А – модуль,
, где А – модуль,  - фаза Þ
- фаза Þ (6.4.4)
(6.4.4) - модули выражений в скобках
- модули выражений в скобках - фаза (сдвиг фазы) выражений в скобках.
- фаза (сдвиг фазы) выражений в скобках. Þ проанализируем изменение фазы (аргумента) скобок при изменении w от нуля до бесконечности Þ
Þ проанализируем изменение фазы (аргумента) скобок при изменении w от нуля до бесконечности Þ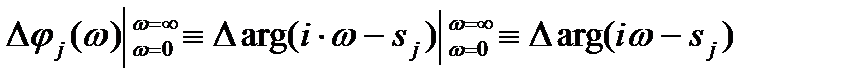 (6.4.5)
(6.4.5) Þ например,
Þ например,  , где
, где  !!!
!!! при изменении
при изменении  Þ
Þ (6.4.6)
(6.4.6)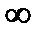 вектор, описывающий скобку
вектор, описывающий скобку 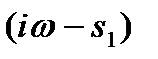 повернется в положительном направлении на угол
повернется в положительном направлении на угол  .
. , где
, где 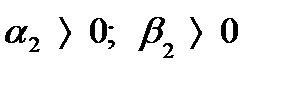
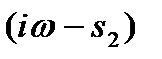 Þ
Þ Þ
Þ Þ
Þ ;
;
 w 0
w 0 (6.4.8)
(6.4.8) ; (комплексно-сопряженный).
; (комплексно-сопряженный).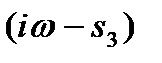 Þ
Þ 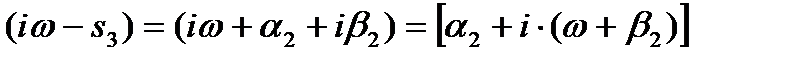 Þ
Þ и т.д. Þ
и т.д. Þ ;
; w 0
w 0 
 Re
Re (6.4.9)
(6.4.9) Þ
Þ (см. формулу 6.4.6), а комплексно-сопряженные полюса в сумме дают
(см. формулу 6.4.6), а комплексно-сопряженные полюса в сумме дают  Þ
Þ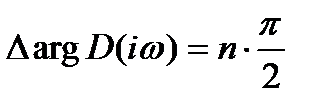 (6.4.9)
(6.4.9)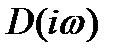 должен поочередно пройти все квадранты в положительном направлении, если САР – устойчива.
должен поочередно пройти все квадранты в положительном направлении, если САР – устойчива. Þ Рассмотрим
Þ Рассмотрим  Þ
Þ очевидно:
очевидно:  и т.д.
и т.д.
 дает вращение вектора
дает вращение вектора 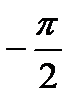 Þ поэтому если первые три скобки
Þ поэтому если первые три скобки 

 «дают поворот» на
«дают поворот» на  , то четвертая скоба на
, то четвертая скоба на 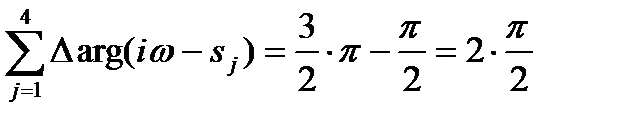 Þ каждый полюс расположенный в правой полуплоскости «дает недоповорот» вектора
Þ каждый полюс расположенный в правой полуплоскости «дает недоповорот» вектора 
 Þ
Þ  Þ
Þ (6.4.11)
(6.4.11) Þ
Þ 

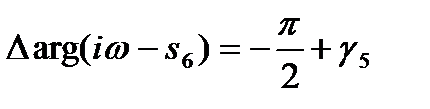 (6.4.12)
(6.4.12) для 5-ой и 6-ой скобок Þ
для 5-ой и 6-ой скобок Þ
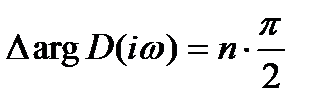 (6.4.13)
(6.4.13) (6.4.14)
(6.4.14) (6.4.15)
(6.4.15)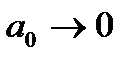 Þ годограф
Þ годограф 
 Þ
Þ
 1
1


