
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация по виду математического описанияСодержание книги
Поиск на нашем сайте
По виду математического описания (уравнений динамики и статики) системы автоматического управления (САУ) подразделяются на линейные и нелинейные системы (САУ или САР). Каждый “подкласс” (линейных и нелинейных) подразделяется на еще ряд “подклассов”. Например, линейные САУ (САР) имеют различия по виду математического описания. Поскольку в этом семестре будут рассматриваться динамические свойства только линейных систем автоматического управления (регулирования), то ниже приведем классификацию по виду математического описания для линейных САУ (САР): 1) Линейные системы автоматического управления, описываемые в переменных «вход-выход» обыкновенными дифференциальными уравнениями (ОДУ) с постоянными коэффициентами:
где x(t) – входное воздействие; y(t) – выходное воздействие (регулируемая величина). Если использовать операторную («компактную») форму записи линейного ОДУ, то уравнение (1.4.1) можно представить в следующем виде:
где p = d/dt - оператор дифференцирования; L (p), N (p) - соответствующие линейные дифференциальные операторы, которые равны:
2) Линейные системы автоматического управления, описываемые линейными обыкновенными дифференциальными уравнениями (ОДУ) с переменными (во времени) коэффициентами:
В общем случае такие системы можно отнести и к классу нелинейных САУ (САР). 3) Линейные системы автоматического управления, описываемые линейными разностными уравнениями:
где f(…) – линейная функция аргументов; k = 1, 2, 3… - целые числа; Dt – интервал квантования (интервал дискретизации). Уравнение (1.4.4) можно представить в «компактной» форме записи
Обычно такое описание линейных САУ (САР) используется в цифровых системах управления (с использованием ЭВМ). 4) Линейные системы автоматического управления с запаздыванием:
где L (p), N (p) - линейные дифференциальные операторы; t - время запаздывания или постоянная запаздывания. Если операторы L (p) и N (p) вырождаются (L (p) = 1; N (p) = 1), то уравнение (1.4.6) соответствует математическому описанию динамики звена идеального запаздывания:
а графическая иллюстрация его свойств представлена на рис. 1.8.
Рис. 1.8 5) Линейные системы автоматического управления, описываемые линейными дифференциальными уравнения в частных производных. Нередко такие САУ называют распределенными системами управления. Þ «Абстрактный» пример такого описания:
Если система управления представляет собой «пространственный» объект, то Þ
где 6) САУ, описываемые системами ОДУ, или системами разностных уравнений, или системами уравнений в частных производных Þ и так далее… Аналогичную классификацию можно предложить и для нелинейных САУ (САР)… Если система уравнений линейна, то необходимы: ü линейность статической характеристики САУ; ü линейность уравнения динамики, т.е. переменные в уравнение динамики входят только в линейной комбинации. Статической характеристикой называется зависимость выхода от величины входного воздействия в установившемся режиме (когда все переходные процессы затухли). Для систем, описываемых линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами статическая характеристика получается из уравнения динамики (1.4.1) приравниванием нулю всех нестационарных членов Þ
На рис.1.9 представлены примеры линейной и нелинейных статических характеристик систем автоматического управления (регулирования).
Рис. 1.9 Нелинейность членов, содержащих производные по времени в уравнениях динамики, может возникнуть при использовании нелинейных математических операций (*, /,
отметим, что в этом уравнении при линейной статической характеристике (
|
||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 (1.4.1)
(1.4.1) , (1.4.2)
, (1.4.2) (1.4.2.а)
(1.4.2.а) (1.4.2.б)
(1.4.2.б)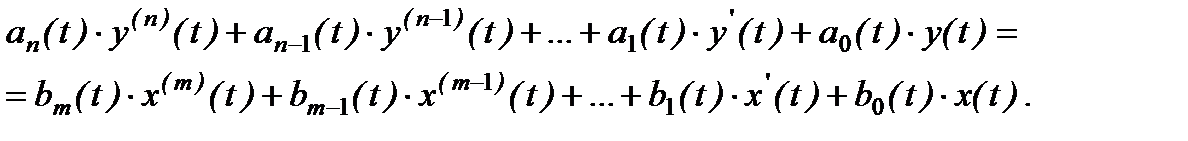 (1.4.3)
(1.4.3)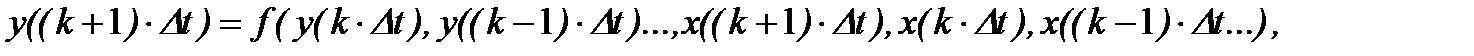 (1.4.4)
(1.4.4) (1.4.5)
(1.4.5)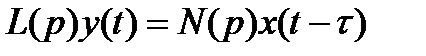 , (1.4.6)
, (1.4.6)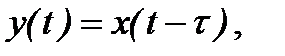

 Система уравнений (1.4.7) описывает динамику линейно распределенной САУ, т.е. регулируемая величина зависит не только от времени, но и от одной пространственной координаты.
Система уравнений (1.4.7) описывает динамику линейно распределенной САУ, т.е. регулируемая величина зависит не только от времени, но и от одной пространственной координаты.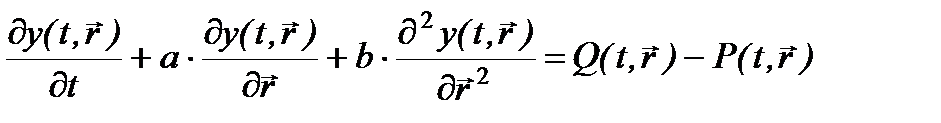 , (1.4.8)
, (1.4.8) зависит от времени и пространственных координат, определяемых радиусом-вектором
зависит от времени и пространственных координат, определяемых радиусом-вектором 
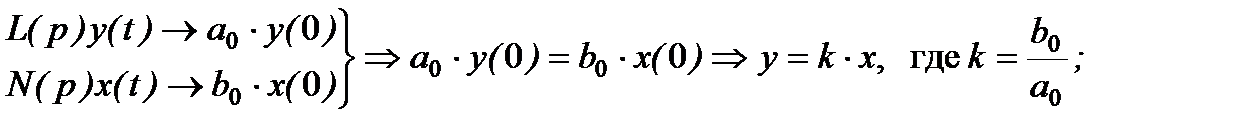

 ,
,  , sin, ln и т.д.). Например, рассматривая уравнение динамики некоторой «абстрактной» САУ
, sin, ln и т.д.). Например, рассматривая уравнение динамики некоторой «абстрактной» САУ
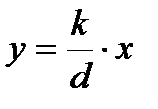 ) второе и третье слагаемые (динамические члены) в левой части уравнения - нелинейные, поэтому САУ, описываемая подобным уравнением, является нелинейной в динамическом плане.
) второе и третье слагаемые (динамические члены) в левой части уравнения - нелинейные, поэтому САУ, описываемая подобным уравнением, является нелинейной в динамическом плане.


